1.9: The function arg(z)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Many-to-one functions
The function f(z)=z2 maps ±z to the same value, e.g. f(2)=f(−2)=4. We say that f(z) is a 2-to-1 function. That is, it maps 2 different points to each value. (Technically, it only maps one point to 0, but we will gloss over that for now.) Here are some other examples of many-to-one functions.
w=z3 is a 3-to-1 function. For example, 3 different z values get mapped to w=1:
13=(−1+√3i2)3=(−1−√3i2)3=1
The function w=ez maps infinitedly many points to each value. For example
e0=e2πi=e4πi=...=e2nπi=...=1
eiπ/2=eiπ/2+2πi=eiπ/2+4πi=...=eiπ/2+2nπi=...=1
In general, ez+2nπi has the same value for every integer n.
Branches of arg(z)
You should master this section. Branches of arg(z) are the key that really underlies all our other examples. Fortunately it is reasonably straightforward.
The key point is that the argument is only defined up to multiples of 2πi so every z produces infinitely many values for arg(z). Because of this we will say that arg(z) is a multiple-valued function.
In general a function should take just one value. What that means in practice is that whenever we use such a function will have to be careful to specify which of the possible values we mean. This is known as specifying a branch of the function.
By a branch of the argument function we mean a choice of range so that it becomes single-valued. By specifying a branch we are saying that we will take the single value of arg(z) that lies in the branch.
Let’s look at several different branches to understand how they work:
(i). If we specify the branch as 0≤arg(z)<2π then we have the following arguments.
arg(1)=0; arg(i)=π/2; arg(−1)=π; arg(−i)=3π/2
This branch and these points are shown graphically in Figure (i) below.
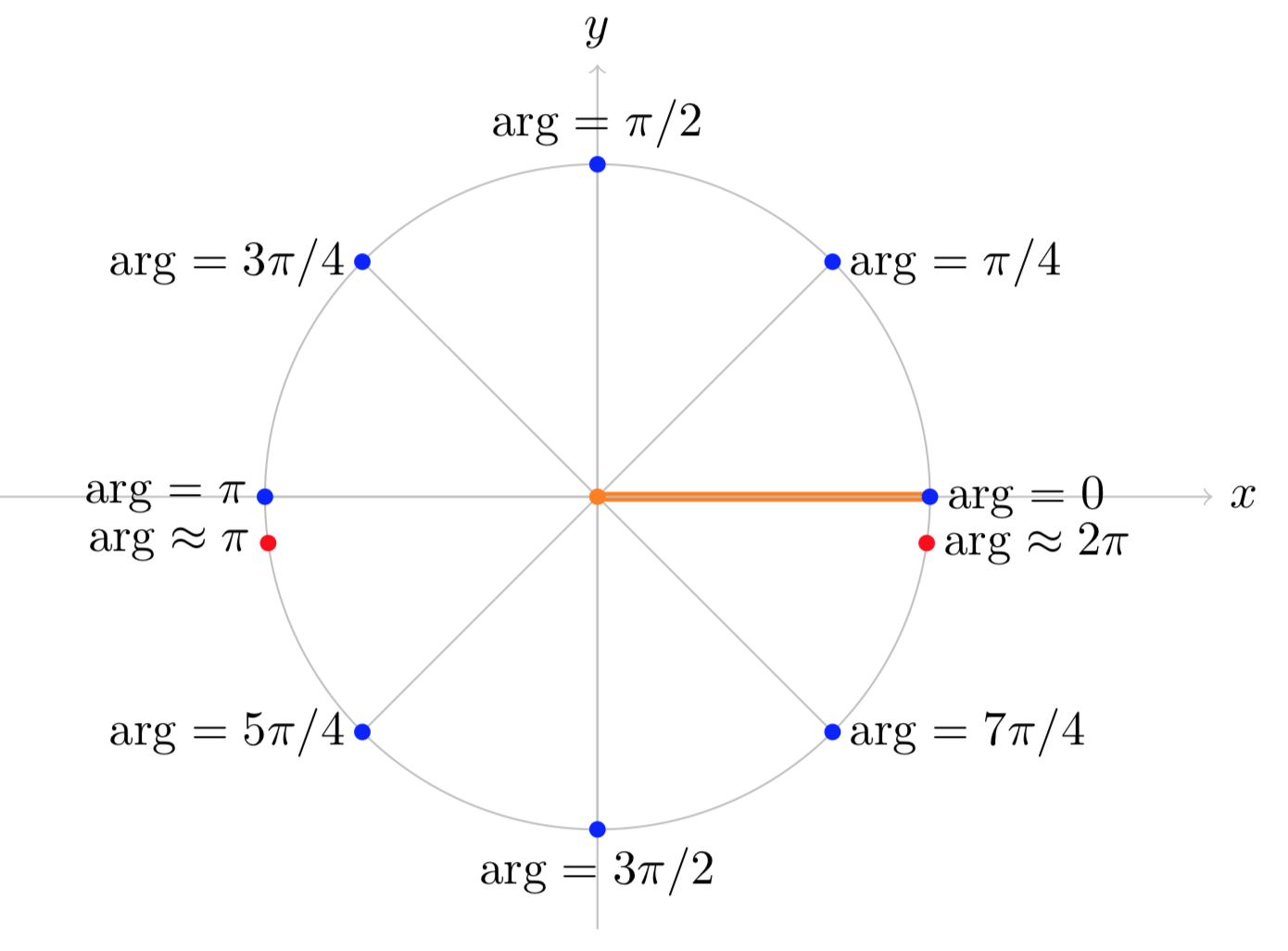
Figure (i): The branch 0≤arg(z)<2π of \text{arg} (z)\).
Notice that if we start at z=1 on the positive real axis we have arg(z)=0. Then arg(z) increases as we move counterclockwise around the circle. The argument is continuous until we get back to the positive real axis. There it jumps from almost 2π back to 0.
There is no getting around (no pun intended) this discontinuity. If we need arg(z) to be continuous we will need to remove (cut) the points of discontinuity out of the domain. The branch cut for this branch of arg(z) is shown as a thick orange line in the figure. If we make the branch cut then the domain for arg(z) is the plane minus the cut, i.e. we will only consider arg(z) for z not on the cut.
For future reference you should note that, on this branch, arg(z) is continuous near the negative real axis, i.e. the arguments of nearby points are close to each other.
(ii). If we specify the branch as −π<arg(z)≤π then we have the following arguments:
arg(1)=0; arg(i)=π/2; arg(−1)=π; arg(−i)=−π/2
This branch and these points are shown graphically in Figure (ii) below.
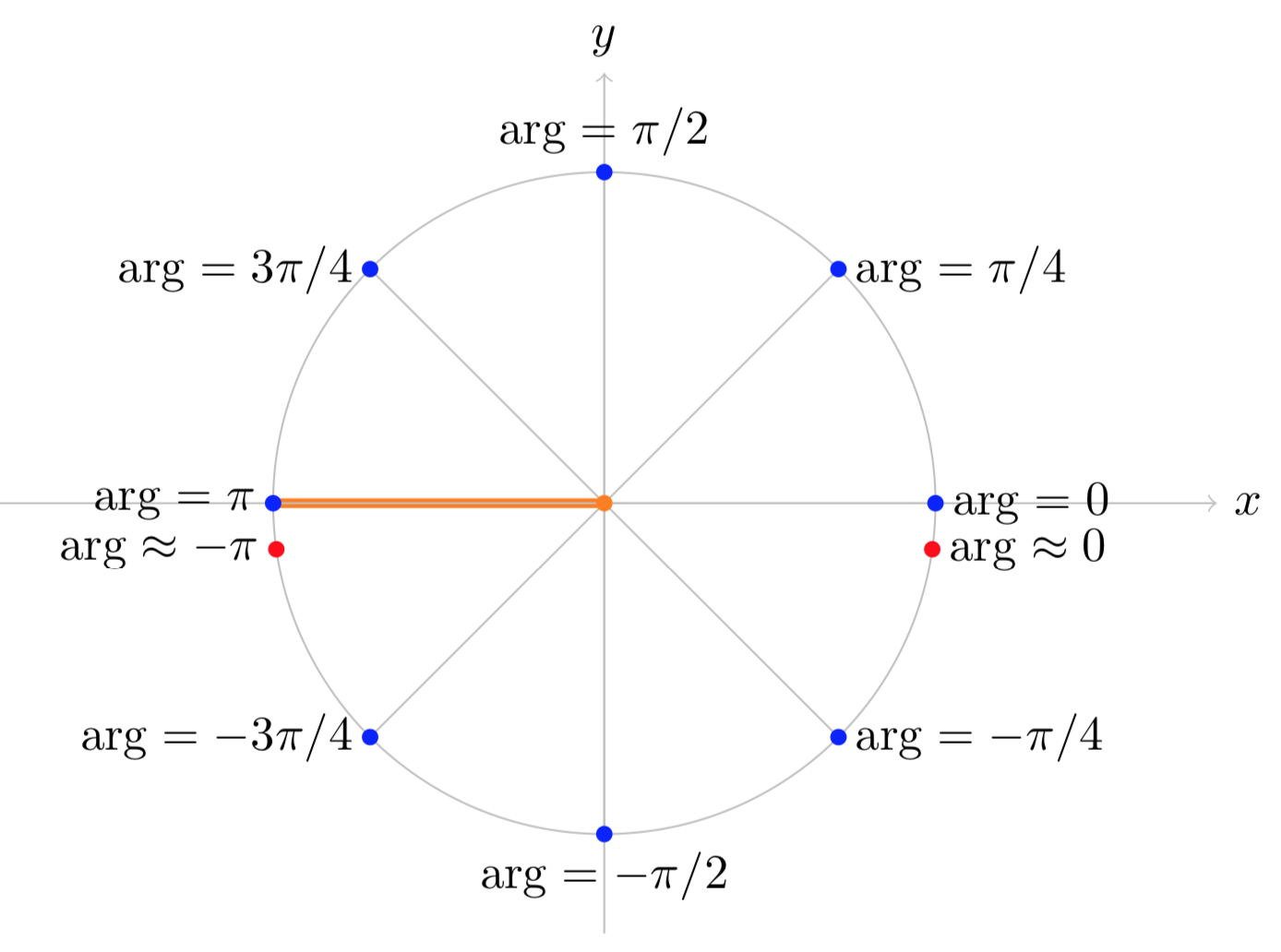
Figure (ii): The branch −π<arg(z)≤π of arg(z).
Compare Figure (ii) with Figure (i). The values of arg(z) are the same in the upper half plane, but in the lower half plane they differ by 2π.
For this branch the branch cut is along the negative real axis. As we cross the branch cut the value of arg(z) jumps from π to something close to −π.
(iii). Figure (iii) shows the branch of arg(z) with π/4≤arg(z)<9π/4.
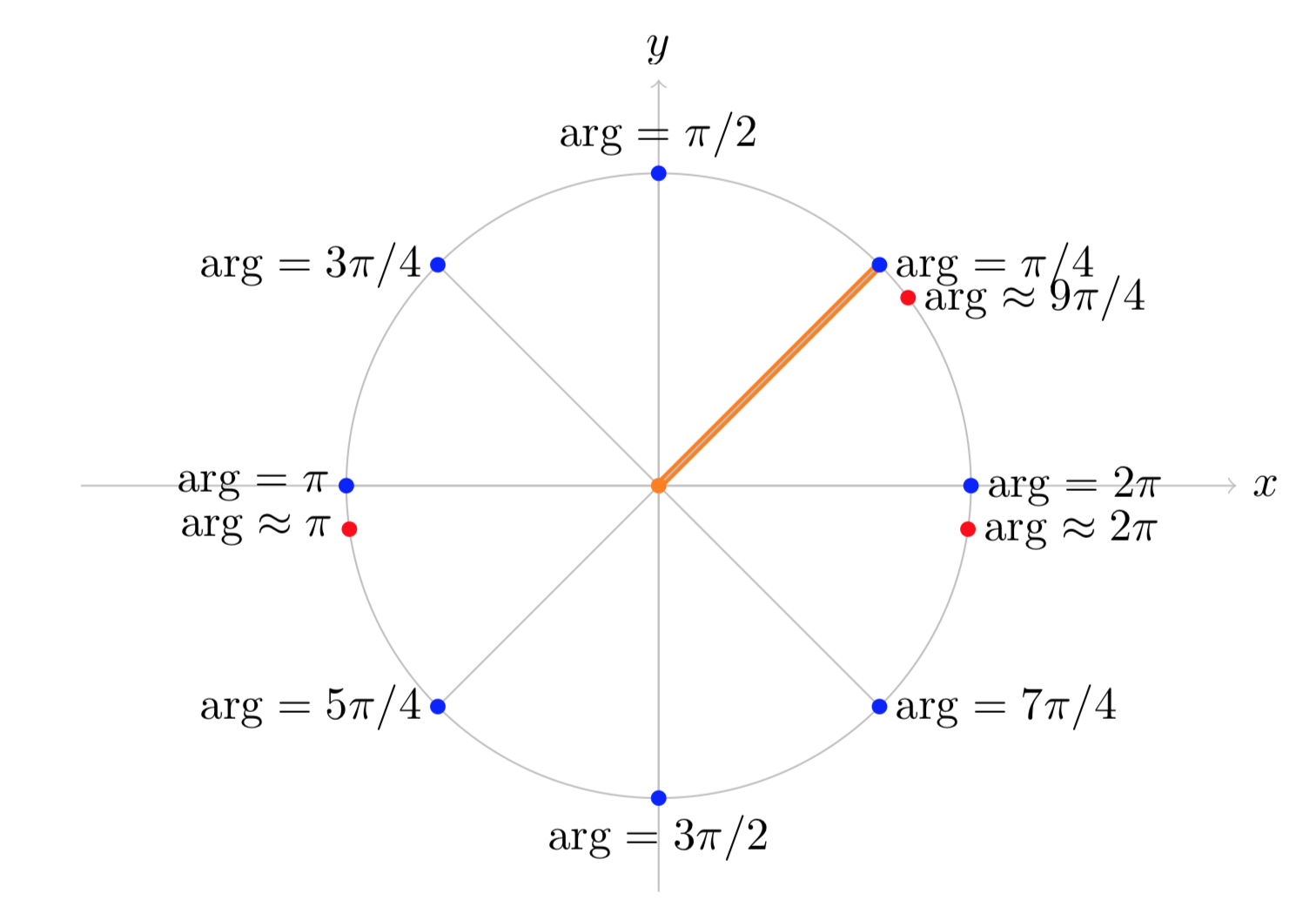
Figure (iii): The branch π/4≤arg(z)<9π/4 of arg(z).
Notice that on this branch arg(z) is continuous at both the positive and negative real axes. The jump of 2π occurs along the ray at angle π/4.
(iv). Obviously, there are many many possible branches. For example,
42<arg(z)≤42+2π.
(v). We won’t make use of this in 18.04, but, in fact, the branch cut doesn’t have to be a straight line. Any curve that goes from the origin to infinity will do. The argument will be continuous except for a jump by 2π when z crosses the branch cut.
principal branch of arg(z)
Branch (ii) in the previous section is singled out and given a name:
The branch −π<arg(z)≤π is called the principal branch of arg(z). We will use the notation Arg(z) (capital A) to indicate that we are using the principal branch. (Of course, in cases where we don’t want there to be any doubt we will say explicitly that we are using the principal branch.)
Continuity of arg(z)
The examples above show that there is no getting around the jump of 2π as we cross the branch cut. This means that when we need arg(z) to be continuous we will have to restrict its domain to the plane minus a branch cut.

