2.9: Branch Cuts and Function Composition
- Page ID
- 45406
We often compose functions, i.e. \(f(g(z))\). In general in this case we have the chain rule to compute the derivative. However we need to specify the domain for \(z\) where the function is analytic. And when branches and branch cuts are involved we need to take care.
Let \(f(z) = e^{z^2}\). Since \(e^z\) and \(z^2\) are both entire functions, so is \(f(z) = e^{z^2}\). The chain rule gives us
\[f'(z) = e^{z^2} (2z).\]
Let \(f(z) = e^z\) and \(g(z) = 1/z\). \(f(z)\) is entire and \(g(z)\) is analytic everywhere but 0. So \(f(g(z))\) is analytic except at 0 and
\(C\) - { \(2\pi n i\), where \(n\) is any integer }
The quotient rule gives \(h'(z) = -e^z/(e^z - 1)^2\). A little more formally: \(h(z) = f(g(z))\). where \(f(w) = 1/w\) and \(w = g(z) = e^z - 1\). We know that \(g(z)\) is entire and \(f(w)\) is analytic everywhere except \(w = 0\). Therefore, \(f(g(z))\) is analytic everywhere except where \(g(z) = 0\).
It can happen that the derivative has a larger domain where it is analytic than the original function. The main example is \(f(z) = \log (z)\). This is analytic on \(C\) minus a branch cut. However
\[\dfrac{d}{dz} \log (z) = \dfrac{1}{z}\]
is analytic on \(C\) - {0}. The converse can’t happen.
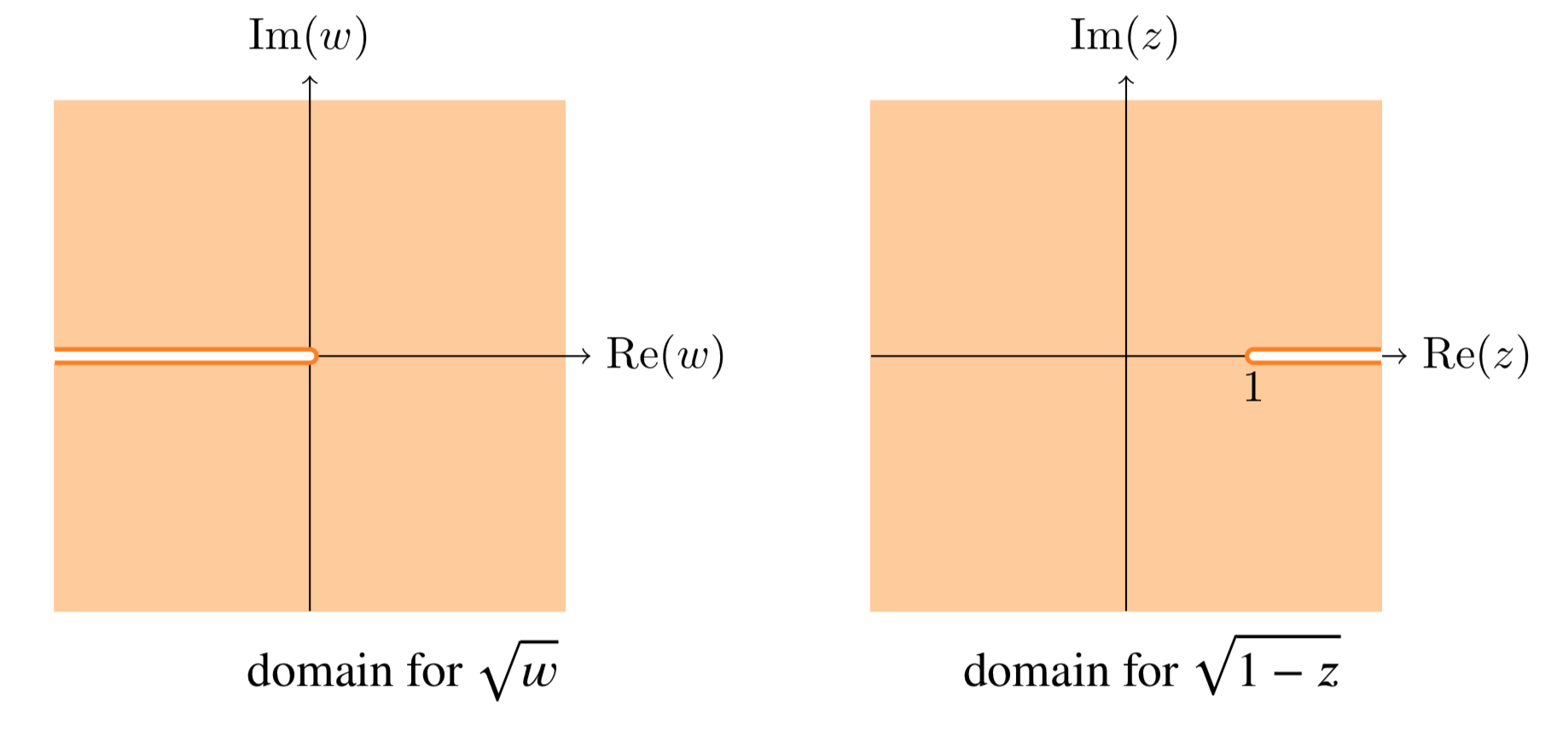
Define a region where \(\sqrt{1 - z}\) is analytic.
Solution
Choosing the principal branch of argument, we have \(\sqrt{w}\) is analytic on
\(C - \{ x \le 0, y = 0\}\), (see figure below.).
So \(\sqrt{1 - z}\) is analytic except where \(w = 1 - z\) is on the branch cut, i.e. where \(w = 1 - z\) is real and \(\le 0\). It's easy to see that
\(w = 1 - z\) is real and \(\le 0\) \(\Leftrightarrow\) \(z\) is real and \(\ge 1\).
So \(\sqrt{1 - z}\) is analytic on the region (see figure below)
\[C - \{x \ge 1, y = 0\}\]
A different branch choice for \(\sqrt{w}\) would lead to a different region where \(\sqrt{1 - z}\) is analytic.
The figure below shows the domains with branch cuts for this example.
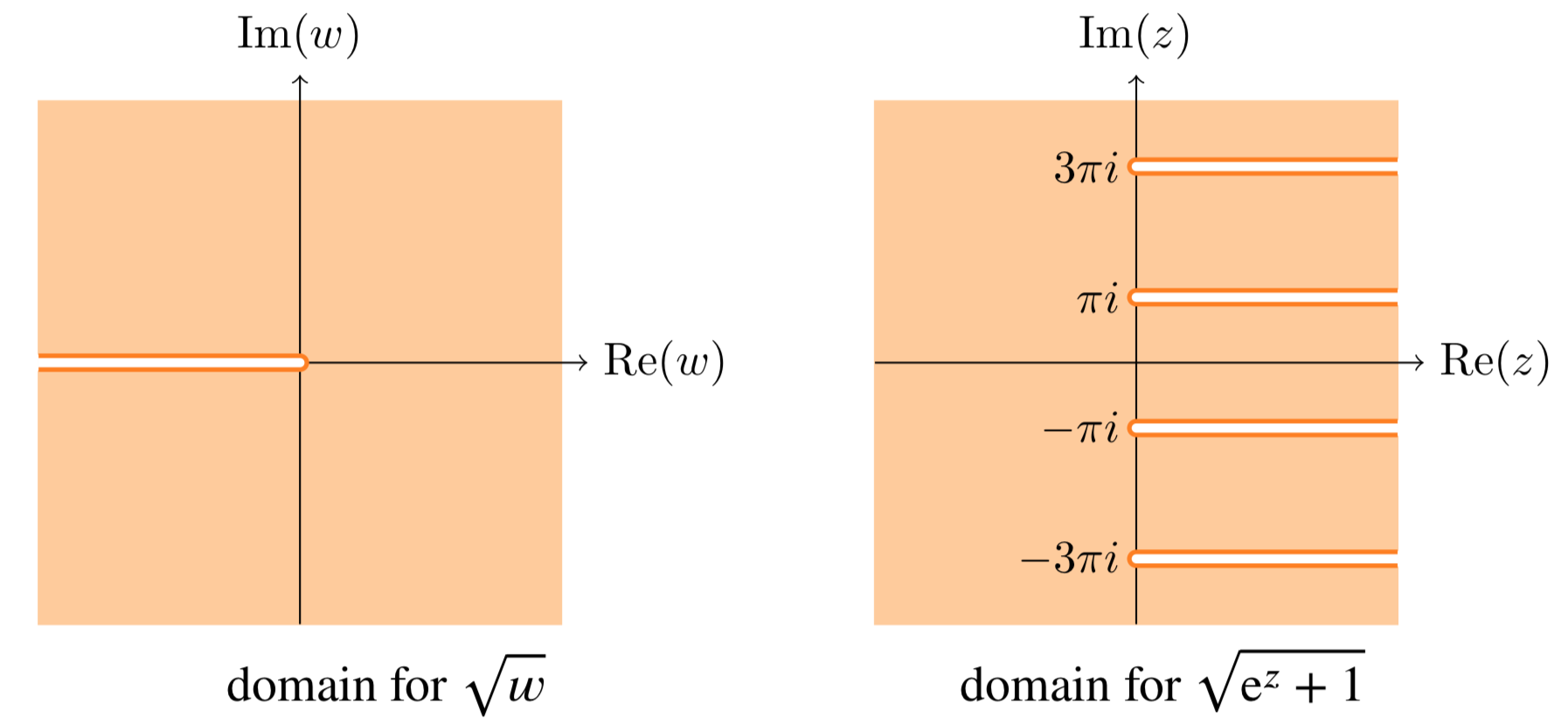
Define a region where \(f(z) = \sqrt{1 + e^z}\) is analytic.
Solution
Again, let's take \(\sqrt{w}\) to be analytic on the region
\[C - \{x \le 0, y = 0\}\]
So, \(f(z)\) is analytic except where \(1 + e^z\) is real and \(\le 0\). That is, except where \(e^z\) is real and \(\le -1\). Now, \(e^z = e^x e^{iy}\) is real only when \(y\) is a multiple of \(\pi\). It is negative only when \(y\) is an odd mutltiple of \(\pi\). It has magnitude greater than 1 only when \(x > 0\). Therefore \(f(z)\) is analytic on the region
\[C - \{x \ge 0, y = \text{odd multiple of } \pi \}\]
The figure below shows the domains with branch cuts for this example.
