5.2: Derivatives of Extended-Real Functions

For a while (in §§2 and 3), we limit ourselves to extended-real functions. Below, $f$ and $g$ are real or extended real (f, $g : E^{1} \rightarrow E^{*}).$ We assume, however, that they are not constantly infinite on any interval $(a, b), a<b$.

Lemma $\PageIndex{1}$

If $f^{\prime}(p)>0$ at some $p \in E^{1},$ then

$$x<p<y$$

implies

$$f(x)<f(p)<f(y)$$

for all $x, y$ in a sufficiently small globe $G_{p}(\delta)=(p-\delta, p+\delta).$

Similarly, if $f^{\prime}(p)<0,$ then $x<p<y$ implies $f(x)>f(p)>f(y)$ for $x, y$ in some $G_{p}(\delta).$

Proof

If $f^{\prime}(p)>0,$ the "0" case in Definition 1 of §1, is excluded, so

$$f^{\prime}(p)=\lim _{x \rightarrow p} \frac{\Delta f}{\Delta x}>0.$$

Hence we must also have $\Delta f / \Delta x>0$ for $x$ in some $G_{p}(\delta)$.

It follows that $\Delta f$ and $\Delta x$ have the same sign in $G_{p}(\delta);$ i.e.,

$$f(x)-f(p)>0 \text { if } x>p \text { and } f(x)-f(p)<0 \text { if } x<p.$$

(This implies $f(p) \neq \pm \infty.$ Why? Hence

$$x<p<y \Longrightarrow f(x)<f(p)<f(y),$$

as claimed; similarly in case $f^{\prime}(p)<0. \quad \square$

Corollary $\PageIndex{1}$

If $f(p)$ is the maximum or minimum value of $f(x)$ for $x$ in some $G_{p}(\delta),$ then $f^{\prime}(p)=0;$ i.e., $f$ has a zero derivative, or none at all, at $p.$

For, by Lemma 1, $f^{\prime}(p) \neq 0$ excludes a maximum or minimum at $p.$ (Why?)

Note 1. Thus $f^{\prime}(p)=0$ is a necessary condition for a local maximum or minimum at $p.$ It is insufficient, however. For example, if $f(x)=x^{3}, f$ has no maxima or minima at all, yet $f^{\prime}(0)=0 .$ For sufficient conditions, see §6.

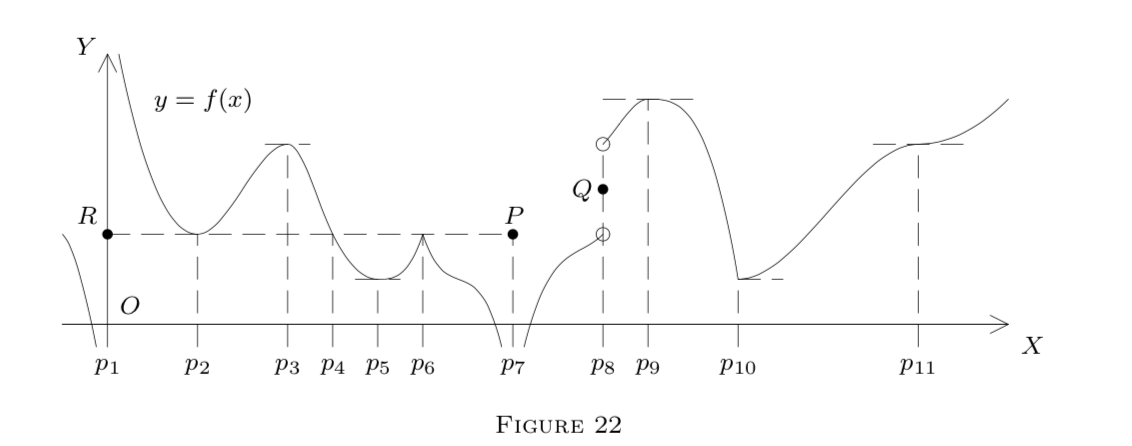
Figure 22 illustrates these facts at the points $p_{2}, p_{3}, \ldots, p_{11}.$ Note that in Figure 22, the isolated points $P, Q, R$ belong to the graph.

Geometrically, $f^{\prime}(p)=0$ means that the tangent at $p$ is horizontal, or that a two-sided tangent does not exist at $p.$

Theorem $\PageIndex{1}$

Let $f : E^{1} \rightarrow E^{*}$ be relatively continuous on an interval $[a, b]$, with $f^{\prime} \neq 0$ on $(a, b).$ Then $f$ is strictly monotone on $[a, b],$ and $f^{\prime}$ is signconstant there (possibly 0 at a and b), with $f^{\prime} \geq 0$ if $f \uparrow,$ and $f^{\prime} \leq 0$ if $f \downarrow$.

Proof

By Theorem 2 of Chapter 4, §8, $f$ attains a least value $m,$ and a largest value $M,$ at some points of $[a, b].$ However, neither can occur at an interior point $p \in(a, b),$ for, by Corollary 1, this would imply $f^{\prime}(p)=0,$ contrary to our assumption.

Thus $M=f(a)$ or $M=f(b);$ for the moment we assume $M=f(b)$ and $m=f(a).$ We must have $m<M,$ for $m=M$ would make $f$ constant on $[a, b]$, implying $f^{\prime}=0.$ Thus $m=f(a)<f(b)=M.$

Now let $a \leq x<y \leq b$. Applying the previous argument to each of the intervals $[a, x],[a, y],[x, y],$ and $[x, b]$ (now using that $m=f(a)<f(b)=M )$, we find that

$$f(a) \leq f(x)<f(y) \leq f(b). \quad \text { (Why?) }$$

Thus $a \leq x<y \leq b$ implies $f(x)<f(y);$ i.e., $f$ increases on $[a, b].$ Hence $f^{\prime}$ cannot be negative at any $p \in[a, b],$ for, otherwise, by Lemma 1, $f$ would decrease at $p.$ Thus $f^{\prime} \geq 0$ on $[a, b].$

In the case $M=f(a)>f(b)=m,$ we would obtain $f^{\prime} \leq 0$. $\quad \square$

Caution: The function $f$ may increase or decrease at $p$ even if $f^{\prime}(p)=0.$
See Note 1.

Corollary $\PageIndex{2}$ (Rolle's theorem)

If : $E^{1} \rightarrow E^{*}$ is relatively continuous on $[a, b]$ and if $f(a)=f(b),$ then $f^{\prime}(p)=0$ for at least one interior point $p \in(a, b)$.

For, if $f^{\prime} \neq 0$ on all of $(a, b),$ then by Theorem 1, $f$ would be strictly monotone on $[a, b],$ so the equality $f(a)=f(b)$ would be impossible.

Figure 22 illustrates this on the intervals $\left[p_{2}, p_{4}\right]$ and $\left[p_{4}, p_{6}\right],$ with $f^{\prime}\left(p_{3}\right)=$ $f^{\prime}\left(p_{5}\right)=0.$ A discontinuity at 0 causes an apparent failure on $[0, p_{2}].$

Note 2. Theorem 1 and Corollary 2 hold even if $f(a)$ and $f(b)$ are infinite, if continuity is interpreted in the sense of the metric $\rho^{\prime}$ of Problem 5 in Chapter 3, §11. (Weierstrass' Theorem 2 of Chapter 4, §8 applies to $\left(E^{*}, \rho^{\prime}\right),$ with the same proof.)

Theorem $\PageIndex{2}$ (Cauchy's law of the mean)

Let the functions $f, g : E^{1} \rightarrow E^{*}$ be relatively continuous and finite on $[a, b]$ and have derivatives on $(a, b),$ with $f^{\prime}$ and $g^{\prime}$ never both infinite at the same point $p \in(a, b).$ Then

$$g^{\prime}(q)[f(b)-f(a)]=f^{\prime}(q)[g(b)-g(a)] \text { for at least one } q \in(a, b).$$

Proof

Let $A=f(b)-f(a)$ and $B=g(b)-g(a).$ We must show that $A g^{\prime}(q)=B f^{\prime}(q)$ for some $q \in(a, b)$. For this purpose, consider the function $h=A g-B f$. It is relatively continuous and finite on $[a, b],$ as are $g$ and $f.$ Also,

$$h(a)=f(b) g(a)-g(b) f(a)=h(b) . \quad \text { (Verify!) }$$

Thus by Corollary 2, $h^{\prime}(q)=0$ for some $q \in(a, b).$ Here, by Theorem 4 of §1, $h^{\prime}=(A g-B f)^{\prime}=A g^{\prime}-B f^{\prime}.$ (This is legitimate, for, by assumption, $f^{\prime}$ and $g^{\prime}$ never both become infinite, so no indeterminate limits occur.) Thus $h^{\prime}(q)=A g^{\prime}(q)-B f^{\prime}(q)=0,$ and (1) follows. $\quad \square$

Corollary $\PageIndex{3}$ (Lagrange's law of the mean)

If $f : E^{1} \rightarrow E^{1}$ is relatively continuous on $[a, b]$ with a derivative on $(a, b),$ then

$$f(b)-f(a)=f^{\prime}(q)(b-a) \text { for at least one } q \in(a, b).$$

Proof

Take $g(x)=x$ in Theorem 2, so $g^{\prime}=1$ on $E^{1}. \square$

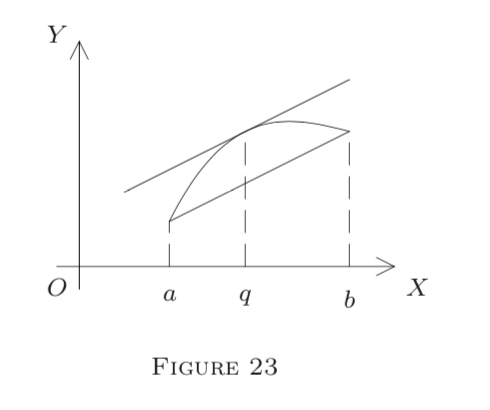
Note 3. Geometrically,

$$\frac{f(b)-f(a)}{b-a}$$

is the slope of the secant through $(a, f(a))$ and $(b, f(b)),$ and $f^{\prime}(q)$ is the slope of the tangent line at $q.$ Thus Corollary 3 states that the secant is parallel to the tangent at some intermediate point $q;$ see Figure 23. Theorem 2 states the same for curves given parametrically: $x=f(t), y=g(t)$.

Corollary $\PageIndex{4}$

Let $f$ be as in Corollary 3. Then

(i) $f$ is constant on $[a, b]$ iff $f^{\prime}=0$ on $(a, b)$;

(ii) $f \uparrow$ on $[a, b]$ iff $f^{\prime} \geq 0$ on $(a, b);$ and

(iii) $f \downarrow$ on $[a, b]$ iff $f^{\prime} \leq 0$ on $(a, b)$.

Proof

Let $f^{\prime}=0$ on $(a, b).$ If $a \leq x \leq y \leq b,$ apply Corollary 3 to the interval $[x, y]$ to obtain

$$f(y)-f(x)=f^{\prime}(q)(y-x) \text { for some } q \in(a, b) \text { and } f^{\prime}(q)=0.$$

Thus $f(y)-f(x)=0$ for $x, y \in[a, b],$ so $f$ is constant.

The rest is left to the reader. $\quad \square$

Theorem $\PageIndex{3}$ (inverse functions)

Let $f : E^{1} \rightarrow E^{1}$ be relatively continuous and strictly monotone on an interval $I \subseteq E^{1}$. Let $f^{\prime}(p) \neq 0$ at some interior point $p \in I.$ Then the inverse function $g=f^{-1}$ (with $f$ restricted to $I)$ has a derivative at $q=f(p),$ and

$$g^{\prime}(q)=\frac{1}{f^{\prime}(p)}.$$

(If $f^{\prime}(p)=\pm \infty,$ then $g^{\prime}(q)=0.)$

Proof

By Theorem 3 of Chapter 4, §9, $g=f^{-1}$ is strictly monotone and relatively continuous on $f[I],$ itself an interval. If $p$ is interior to $I,$ then $q=f(p)$ is interior to $f[I].$ (Why?)

Now if $y \in f[I],$ we set

$$\Delta g=g(y)-g(q), \Delta y=y-q, x=f^{-1}(y)=g(y), \text { and } f(x)=y$$

and obtain

$$\frac{\Delta g}{\Delta y}=\frac{g(y)-g(q)}{y-q}=\frac{x-p}{f(x)-f(p)}=\frac{\Delta x}{\Delta f} \text { for } x \neq p.$$

Now if $y \rightarrow q,$ the continuity of $g$ at $q$ yields $g(y) \rightarrow g(q);$ i.e., $x \rightarrow p.$ Also, $x \neq p$ iff $y \neq q$, for $f$ and $g$ are one-to-one functions. Thus we may substitute $y=f(x)$ or $x=g(y)$ to get

$$g^{\prime}(q)=\lim _{y \rightarrow q} \frac{\Delta g}{\Delta y}=\lim _{x \rightarrow p} \frac{\Delta x}{\Delta f}=\frac{1}{\lim _{x \rightarrow p}(\Delta f / \Delta x)}=\frac{1}{f^{\prime}(p)},$$

where we use the convention $\frac{1}{\infty}=0$ if $f^{\prime}(p)=\infty. \quad \square$

Examples

(A) Let

$$f(x)=\log _{a}|x| \text { with } f(0)=0.$$

Let $p>0.$ Then $(\forall x>0)$

$$\begin{aligned} \Delta f &=f(x)-f(p)=\log _{a} x-\log _{a} p=\log _{a}(x / p) \\ &=\log _{a} \frac{p+(x-p)}{p}=\log _{a}\left(1+\frac{\Delta x}{p}\right). \end{aligned}$$

Thus

$$\frac{\Delta f}{\Delta x}=\log _{a}\left(1+\frac{\Delta x}{p}\right)^{1 / \Delta x}.$$

Now let $z=\Delta x / p.$ (Why is this substitution admissible?) Then using the formula

$$\lim _{z \rightarrow 0}(1+z)^{1 / z}=e \quad \text { (see Chapter 4, §2, Example (C)) }$$

and the continuity of the log and power functions, we obtain

$$f^{\prime}(p)=\lim _{x \rightarrow p} \frac{\Delta f}{\Delta x}=\lim _{z \rightarrow 0} \log _{a}\left[(1+z)^{1 / z}\right]^{1 / p}=\log _{a} e^{1 / p}=\frac{1}{p} \log _{a} e.$$

The same formula results also if $p<0,$ i.e., $|p|=-p.$ At $p=0, f$ has one-sided derivatives $( \pm \infty)$ only (verify!), so $f^{\prime}(0)=0$ by Definition 1 in §1.

(B) The inverse of the log $_{a}$ function is the exponential $g : E^{1} \rightarrow E^{1},$ with

$$g(y)=a^{y} \quad(a>0, a \neq 1).$$

By Theorem 3, we have

$$\left(\forall q \in E^{1}\right) \quad g^{\prime}(q)=\frac{1}{f^{\prime}(p)}, p=g(q)=a^{q}.$$

Thus

$$g^{\prime}(q)=\frac{1}{\frac{1}{p} \log _{a} e}=\frac{p}{\log _{a} e}=\frac{a^{q}}{\log _{a} e}.$$

Symbolically,

$$\left(\log _{a}|x|\right)^{\prime}=\frac{1}{x} \log _{a} e(x \neq 0) ; \quad\left(a^{x}\right)^{\prime}=\frac{a^{x}}{\log _{a} e}=a^{x} \ln a.$$

In particular, if $a=e,$ we have $\log _{e} a=1$ and $\log _{a} x=\ln x ;$ hence

$$(\ln |x|)^{\prime}=\frac{1}{x}(x \neq 0) \quad \text { and } \quad\left(e^{x}\right)^{\prime}=e^{x} \quad\left(x \in E^{1}\right).$$

(C) The power function $g :(0,+\infty) \rightarrow E^{1}$ is given by

$$g(x)=x^{a}=\exp (a \cdot \ln x) \text { for } x>0 \text { and fixed } a \in E^{1}.$$

By the chain rule (§1, Theorem 3), we obtain

$$g^{\prime}(x)=\exp (a \cdot \ln x) \cdot \frac{a}{x}=x^{a} \cdot \frac{a}{x}=a \cdot x^{a-1}.$$

Thus we have the symbolic formula

$$\left(x^{a}\right)^{\prime}=a \cdot x^{a-1} \text { for } x>0 \text { and fixed } a \in E^{1}.$$

Theorem $\PageIndex{4}$ (Darboux)

If $f : E^{1} \rightarrow E^{*}$ is relatively continuous and has a derivative on an interval I, then $f^{\prime}$ has the Darboux property (Chapter 4, §9 ) on $I.$

Proof

Let $p, q \in I$ and $f^{\prime}(p)<c<f^{\prime}(q).$ Put $g(x)=f(x)-c x.$ Assume $g^{\prime} \neq 0$ on $(p, q)$ and find a contradiction to Theorem 1. Details are left to the reader. $\quad \square$