6.6.E: Problems on Bijective Linear Maps and Jacobians
- Page ID
- 24091
(i) Can a functional determinant \(f=\operatorname{det}\left(v_{i k}\right)\) (see Note 1) be continuous or differentiable even if the functions \(v_{i k}\) are not?
(ii) Must a Jacobian map \(J_{f}\) be continuous or differentiable if \(f\) is?
Give proofs or counterexamples.
\(\Rightarrow\) Prove rule (b) on determinants. More generally, show that if \(f(\vec{x})=\vec{x}\) on an open set \(A \subseteq E^{n}\left(C^{n}\right),\) then \(J_{f}=1\) on \(A\).
Let \(f : E^{n} \rightarrow E^{n}\) (or \(C^{n} \rightarrow C^{n}\)), \(f=\left(f_{1}, \ldots, f_{n}\right)\).
Suppose each \(f_{k}\) depends on \(x_{k}\) only, i.e.,
\[f_{k}(\vec{x})=f_{k}(\vec{y}) \text{ if } x_{k}=y_{k},\]
regardless of the other coordinates \(x_{i}, y_{i}.\) Prove that \(J_{f}=\prod_{k=1}^{n} D_{k} f_{k}\).
[Hint: Show that \(D_{k} f_{i}=0\) if \(i \neq k\).]
In Corollary 1, show that
\[J_{h}(\vec{p})=\prod_{k=1}^{n} D_{k} f_{k}(\vec{p}) \cdot J_{g}(\vec{q})\]
if \(f\) also has the property specified in Problem 3. Then do all in "variables," with \(y_{k}=y_{k}\left(x_{k}\right)\) instead of \(f_{k}\).
Let \(E^{\prime}=E^{1}\) in Note 1. Prove that if all the \(v_{i k}\) are differentiable at \(p,\) then \(f^{\prime}(p)\) is the sum of \(n\) determinants, each arising from det \(\left(v_{i k}\right),\) by replacing the terms of one column by their derivatives.
[Hint: Use Problem 6 in Chapter 5, §1.]
Do Problem 5 for partials of \(f,\) with \(E^{\prime}=E^{n}\left(C^{n}\right),\) and for directionals \(D_{\vec{u}} f,\) in any normed space \(E^{\prime}.\) (First, prove formulas analogous to Problem 6 in Chapter 5, §1; use Note 3 in §1.) Finally, do it for the differential, \(d f(\vec{p} ; \cdot).\)
In Note 1 of §4, express the matrices in terms of partials (see Theorem 4 in §3). Invent a "variable" notation for such matrices, imitating Jacobians (Corollary 3).
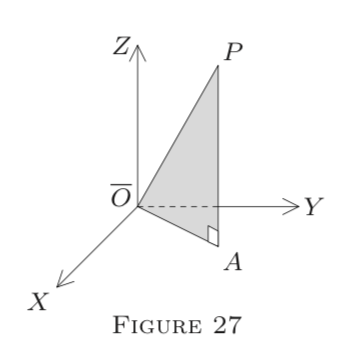
(i) Show that
\[\frac{\partial(x, y, z)}{\partial(r, \theta, \alpha)}=-r^{2} \sin \alpha\]
if
\[\begin{array}{l}{x=r \cos \theta,} \\ {y=r \sin \theta \sin \alpha, \text { and }} \\ {z=r \cos \alpha}\end{array}\]
(This transformation is passage to polars in \(E^{3};\) see Figure 27, where \(r=O P, \angle X O A=\theta,\) and \(\angle A O P=\alpha.)\)
(ii) What if \(x=r \cos \theta, y=r \sin \theta,\) and \(z=z\) remains unchanged (passage to cylindric coordinates)?
(iii) Same for \(x=e^{r} \cos \theta, y=e^{r} \sin \theta,\) and \(z=z\).
Is \(f=\left(f_{1}, f_{2}\right) : E^{2} \rightarrow E^{2}\) one-to-one or bijective, and is \(J_{f} \neq 0,\) if
(i) \(f_{1}(x, y)=e^{x} \cos y\) and \(f_{2}(x, y)=e^{x} \sin y\);
(ii) \(f_{1}(x, y)=x^{2}-y^{2}\) and \(f_{2}(x, y)=2 x y ?\)
Define \(f : E^{3} \rightarrow E^{3}\) (or \(C^{3} \rightarrow C^{3}\))
\[f(\vec{x})=\frac{\vec{x}}{1+\sum_{k=1}^{3} x_{k}}\]
on
\[A=\left\{\vec{x} | \sum_{k=1}^{3} x_{k} \neq-1\right\}\]
and \(f=\overrightarrow{0}\) on \(-A.\) Prove the following.
(i) \(f\) is one-to-one on \(A\) (find \(f^{-1}!\)).
(ii) \(J_{f}(\vec{x})=\frac{1}{\left(1+\sum_{k=1}^{3} x_{k}\right)^{4}}\).
(iii) Describe \(-A\) geometrically.
Given any sets \(A, B\) and maps \(f, g : A \rightarrow E^{\prime}, h : E^{\prime} \rightarrow E,\) and \(k : B \rightarrow A,\) prove that
(i) \((f \pm g) \circ k=f \circ k \pm g \circ k,\) and
(ii) \(h \circ(f \pm g)=h \circ f \pm h \circ g\) if \(h\) is linear.
Use these distributive laws to verify that
\[\phi^{-1} \circ(\theta-\phi) \circ \theta^{-1}=\phi^{-1}-\theta^{-1}\]
In Corollary 3.
[Hint: First verify the associativity of mapping composition.]
Prove that if \(\phi : E^{\prime} \rightarrow E\) is linear and one-to-one, so is \(\phi^{-1} : E^{\prime \prime} \rightarrow E^{\prime},\) where \(E^{\prime \prime}=\phi\left[E^{\prime}\right].\)
Let \(\vec{v}_{1}, \ldots, \vec{v}_{n}\) be the column vectors in \(\operatorname{det}[\phi].\) Prove that \(\operatorname{det}[\phi]\) turns into
(i) \(c \cdot \operatorname{det}[\phi]\) if one of the \(\vec{v}_{k}\) is multiplied by a scalar \(c\);
(ii) \(-\operatorname{det}[\phi],\) if any two of the \(\vec{v}_{k}\) are interchanged (consider \(\lambda\) in formula (1)).
Furthermore, show that
(iii) \(\operatorname{det}[\phi]\) does not change if some \(\vec{v}_{k}\) is replaced by \(\vec{v}_{k}+c \vec{v}_{i}(i \neq k)\);
(iv) \(\operatorname{det}[\phi]=0\) if some \(\vec{v}_{k}\) is \(\overrightarrow{0},\) or if two of the \(\vec{v}_{k}\) are the same.

