6.7: Inverse and Implicit Functions. Open and Closed Maps

I. "If \(f \in C D^{1}\) at \(\vec{p},\) then \(f\) resembles a linear map (namely \(d f )\) at \(\vec{p}."\) Pursuing this basic idea, we first make precise our notion of "\(f \in C D^{1}\) at \(\vec{p}\)."

Definition 1

A map \(f : E^{\prime} \rightarrow E\) is continuously differentiable, or of class \(C D^{1}\) (written \(f \in C D^{1}),\) at \(\vec{p}\) iff the following statement is true:

\[\begin{array}{l}{\text { Given any } \varepsilon>0, \text { there is } \delta>0 \text { such that } f \text { is differentiable on the }} \\ {\text { globe } \overline{G}=\overline{G_{\vec{p}}(\delta)}, \text { with }} \\ {\qquad\|d f(\vec{x} ; \cdot)-d f(\vec{p} ; \cdot)\|<\varepsilon \text { for all } \vec{x} \in \overline{G}.}\end{array}\]

By Problem 10 in §5, this definition agrees with Definition 1 §5, but is no longer limited to the case \(E^{\prime}=E^{n}\left(C^{n}\right).\) See also Problems 1 and 2 below.

We now obtain the following result.

Theorem \(\PageIndex{1}\)

Let \(E^{\prime}\) and \(E\) be complete. If \(f : E^{\prime} \rightarrow E\) is of class \(C D^{1}\) at \(\vec{p}\) and if \(d f(\vec{p} ; \cdot)\) is bijective (§6), then \(f\) is one-to-one on some globe \(\overline{G}=\overline{G_{\vec{p}}}(\delta).\)

Thus \(f\) "locally" resembles df \((\vec{p} ; \cdot)\) in this respect.

Proof

Set \(\phi=d f(\vec{p} ; \cdot)\) and

\[\left\|\phi^{-1}\right\|=\frac{1}{\varepsilon}\]

(cf. Theorem 2 of §6).

By Definition 1, fix \(\delta>0\) so that for \(\vec{x} \in \overline{G}=\overline{G_{\vec{p}}(\delta)}\).

\[\|d f(\vec{x} ; \cdot)-\phi\|<\frac{1}{2} \varepsilon.\]

Then by Note 5 in §2,

\[(\forall \vec{x} \in \overline{G})\left(\forall \vec{u} \in E^{\prime}\right) \quad|d f(\vec{x} ; \vec{u})-\phi(\vec{u})| \leq \frac{1}{2} \varepsilon|\vec{u}|.\]

Now fix any \(\vec{r}, \vec{s} \in \overline{G}, \vec{r} \neq \vec{s},\) and set \(\vec{u}=\vec{r}-\vec{s} \neq 0.\) Again, by Note 5 in §2,

\[|\vec{u}|=\left|\phi^{-1}(\phi(\vec{u}))\right| \leq\left\|\phi^{-1}\right\||\phi(\vec{u})|=\frac{1}{\varepsilon}|\phi(\vec{u})|;\]

so

\[0<\varepsilon|\vec{u}| \leq|\phi(\vec{u})|.\]

By convexity, \(\overline{G} \supseteq I=L[\vec{s}, \vec{r}],\) so (1) holds for \(\vec{x} \in I, \vec{x}=\vec{s}+t \vec{u}, 0 \leq t \leq 1\).

Noting this, set

\[h(t)=f(\vec{s}+t \vec{u})-t \phi(\vec{u}), \quad t \in E^{1}.\]

Then for \(0 \leq t \leq 1\),

\[\begin{aligned} h^{\prime}(t) &=D_{\vec{u}} f(\vec{s}+t \vec{u})-\phi(\vec{u}) \\ &=d f(\vec{s}+t \vec{u} ; \vec{u})-\phi(\vec{u}). \end{aligned}\]

(Verify!) Thus by (1) and (2),

\[\begin{aligned} \sup _{0 \leq t \leq 1}\left|h^{\prime}(t)\right| &=\sup _{0 \leq t \leq 1}|d f(\vec{s}+t \vec{u} ; \vec{u})-\phi(\vec{u})| \\ & \leq \frac{\varepsilon}{2}|\vec{u}| \leq \frac{1}{2}|\phi(\vec{u})|. \end{aligned}\]

(Explain!) Now, by Corollary 1 in Chapter 5, §4,

\[|h(1)-h(0)| \leq(1-0) \cdot \sup _{0 \leq t \leq 1}\left|h^{\prime}(t)\right| \leq \frac{1}{2}|\phi(\vec{u})|.\]

As \(h(0)=f(\vec{s})\) and

\[h(1)=f(\vec{s}+\vec{u})-\phi(\vec{u})=f(\vec{r})-\phi(\vec{u}),\]

we obtain (even if \(\vec{r}=\vec{s})\)

\[|f(\vec{r})-f(\vec{s})-\phi(\vec{u})| \leq \frac{1}{2}|\phi(\vec{u})| \quad(\vec{r}, \vec{s} \in \overline{G}, \vec{u}=\vec{r}-\vec{s}).\]

But by the triangle law,

\[|\phi(\vec{u})|-|f(\vec{r})-f(\vec{s})| \leq|f(\vec{r})-f(\vec{s})-\phi(\vec{u})|.\]

Thus

\[|f(\vec{r})-f(\vec{s})| \geq \frac{1}{2}|\phi(\vec{u})| \geq \frac{1}{2} \varepsilon|\vec{u}|=\frac{1}{2} \varepsilon|\vec{r}-\vec{s}|\]

by (2).

Hence \(f(\vec{r}) \neq f(\vec{s})\) whenever \(\vec{r} \neq \vec{s}\) in \(\overline{G};\) so \(f\) is one-to-one on \(\overline{G},\) as claimed.\(\quad \square\)

Corollary \(\PageIndex{1}\)

Under the assumptions of Theorem 1, the maps \(f\) and \(f^{-1}\) (the inverse of \(f\) restricted to \(\overline{G}\)) are uniformly continuous on \(\overline{G}\) and \(f[\overline{G}],\) respectively.

Proof

By (3),

\[\begin{aligned}|f(\vec{r})-f(\vec{s})| & \leq|\phi(\vec{u})|+\frac{1}{2}|\phi(\vec{u})| \\ & \leq|2 \phi(\vec{u})| \\ & \leq 2\|\phi\||\vec{u}| \\ &=2\|\phi\||\vec{r}-\vec{s}| \quad(\vec{r}, \vec{s} \in \overline{G}). \end{aligned}\]

This implies uniform continuity for \(f\). (Why?)

Next, let \(g=f^{-1}\) on \(H=f[\overline{G}]\).

If \(\vec{x}, \vec{y} \in H,\) let \(\vec{r}=g(\vec{x})\) and \(\vec{s}=g(\vec{y});\) so \(\vec{r}, \vec{s} \in \overline{G},\) with \(\vec{x}=f(\vec{r})\) and \(\vec{y}=f(\vec{s}).\) Hence by (4),

\[|\vec{x}-\vec{y}| \geq \frac{1}{2} \varepsilon|g(\vec{x})-g(\vec{y})|,\]

proving all for \(g,\) too.\(\quad \square\)

Again, \(f\) resembles \(\phi\) which is uniformly continuous, along with \(\phi^{-1}\).

II. We introduce the following definition.

Definition 2

A map \(f :(S, \rho) \rightarrow\left(T, \rho^{\prime}\right)\) is closed (open) on \(D \subseteq S\) iff, for any \(X \subseteq D\) the set \(f[X]\) is closed (open) in \(T\) whenever \(X\) is so in \(S.\)

Note that continuous maps have such a property for inverse images (Problem 15 in Chapter 4, §2).

Corollary \(\PageIndex{2}\)

Under the assumptions of Theorem 1, \(f\) is closed on \(\overline{G},\) and so the set \(f[\overline{G}]\) is closed in \(E.\)

Similarly for the map \(f^{-1}\) on \(f[\overline{G}]\).

Proof for \(E^{\prime}=E=E^{n}\left(C^{n}\right)\) (for the general case, see Problem 6)

Given any closed \(X \subseteq \overline{G},\) we must show that \(f[X]\) is closed in \(E.\)

Now, as \(\overline{G}\) is closed and bounded, it is compact (Theorem 4 of Chapter 4, §6).

So also is \(X\) (Theorem 1 in Chapter 4, §6), and so is \(f[X]\) (Theorem 1 of Chapter 4, §8).

By Theorem 2 in Chapter 4, §6, \(f[X]\) is closed, as required.\(\quad \square\)

For the rest of this section, we shall set \(E^{\prime}=E=E^{n}\left(C^{n}\right)\).

Theorem \(\PageIndex{2}\)

If \(E^{\prime}=E=E^{n}\left(C^{n}\right)\) in Theorem 1, with other assumptions unchanged, then \(f\) is open on the globe \(G=G_{\vec{p}}(\delta),\) with \(\delta\) sufficiently small.

Proof

We first prove the following lemma.

Lemma

\(f[G]\) contains a globe \(G_{\vec{q}}(\alpha)\) where \(\vec{q}=f(\vec{p})\).

Proof

Indeed, let

\[\alpha=\frac{1}{4} \varepsilon \delta,\]

where \(\delta\) and \(\varepsilon\) are as in the proof of Theorem 1. (We continue the notation and formulas of that proof.)

Fix any \(\vec{c} \in G_{\vec{q}}(\alpha);\) so

\[|\vec{c}-\vec{q}|<\alpha=\frac{1}{4} \varepsilon \delta.\]

Set \(h=|f-\vec{c}|\) on \(E^{\prime}.\) As \(f\) is uniformly continuous on \(\overline{G},\) so is \(h\).

Now, \(\overline{G}\) is compact in \(E^{n}\left(C^{n}\right);\) so Theorem 2(ii) in Chapter 4, §8, yields a point \(\vec{r} \in \overline{G}\) such that

\[h(\vec{r})=\min h[\overline{G}].\]

We claim that \(\vec{r}\) is in \(G\) (the interior of \(\overline{G})\).

Otherwise, \(|\vec{r}-\vec{p}|=\delta ;\) for by (4),

\[\begin{aligned} 2 \alpha=\frac{1}{2} \varepsilon \delta=\frac{1}{2} \varepsilon|\vec{r}-\vec{p}| & \leq|f(\vec{r})-f(\vec{p})| \\ & \leq|f(\vec{r})-\vec{c}|+|\vec{c}-f(\vec{p})| \\ &=h(\vec{r})+h(\vec{p}). \end{aligned}\]

But

\[h(\vec{p})=|\vec{c}-f(\vec{p})|=|\vec{c}-\vec{q}|<\alpha;\]

and so (7) yields

\[h(\vec{p})<\alpha<h(\vec{r}),\]

contrary to the minimality of \(h(\vec{r})\) (see (6)). Thus \(|\vec{r}-\vec{p}|\) cannot equal \(\delta\).

We obtain \(|\vec{r}-\vec{p}|<\delta,\) so \(\vec{r} \in G_{\vec{p}}(\delta)=G\) and \(f(\vec{r}) \in f[G].\) We shall now show that \(\vec{c}=f(\vec{r}).\)

To this end, we set \(\vec{v}=\vec{c}-f(\vec{r})\) and prove that \(\vec{v}=\overrightarrow{0}.\) Let

\[\vec{u}=\phi^{-1}(\vec{v}),\]

where

\[\phi=d f(\vec{p} ; \cdot),\]

as before. Then

\[\vec{v}=\phi(\vec{u})=d f(\vec{p} ; \vec{u}).\]

With \(\vec{r}\) as above, fix some

\[\vec{s}=\vec{r}+t \vec{u} \quad(0<t<1)\]

with \(t\) so small that \(\vec{s} \in G\) also. Then by formula (3),

\[|f(\vec{s})-f(\vec{r})-\phi(t \vec{u})| \leq \frac{1}{2}|t \vec{v}|;\]

also,

\[|f(\vec{r})-\vec{c}+\phi(t \vec{u})|=(1-t)|\vec{v}|=(1-t) h(\vec{r})\]

by our choice of \(\vec{v}, \vec{u}\) and \(h.\) Hence by the triangle law,

\[h(\vec{s})=|f(\vec{s})-\vec{c}| \leq\left(1-\frac{1}{2} t\right) h(\vec{r}).\]

(Verify!)

As \(0<t<1,\) this implies \(h(\vec{r})=0\) (otherwise, \(h(\vec{s})<h(\vec{r}),\) violating (6)).

Thus, indeed,

\[|\vec{v}|=|f(\vec{r})-\vec{c}|=0,\]

i.e.,

\[\vec{c}=f(\vec{r}) \in f[G] \quad \text { for } \vec{r} \in G.\]

But \(\vec{c}\) was an arbitrary point of \(G_{\vec{q}}(\alpha).\) Hence

\[G_{\vec{q}}(\alpha) \subseteq f[G],\]

proving the lemma.\(\quad \square\)

Proof of Theorem 2. The lemma shows that \(f(\vec{p})\) is in the interior of \(f[G]\) if \(\vec{p}, f, d f(\vec{p} ; \cdot),\) and \(\delta\) are as in Theorem 1.

But Definition 1 implies that here \(f \in C D^{1}\) on all of \(G\) (see Problem 1).

Also, \(d f(\vec{x} ; \cdot)\) is bijective for any \(\vec{x} \in G\) by our choice of \(G\) and Theorems 1 and 2 in §6.

Thus \(f\) maps all \(\vec{x} \in G\) onto interior points of \(f[G];\) i.e., \(f\) maps any open set \(X \subseteq G\) onto an open \(f[X],\) as required.\(\quad \square\)

Note 1. A map

\[f :(S, \rho) \underset{\text { onto }}{\longleftrightarrow} (T, \rho^{\prime})\]

is both open and closed ("clopen") iff \(f^{-1}\) is continuous - see Problem 15(iv)(v) in Chapter 4, §2, interchanging \(f\) and \(f^{-1}.\)

Thus \(\phi=d f(\vec{p} ; \cdot)\) in Theorem 1 is "clopen" on all of \(E^{\prime}\).

Again, \(f\) locally resembles \(d f(\vec{p} ; \cdot)\).

III. The Inverse Function Theorem. We now further pursue these ideas.

Theorem \(\PageIndex{3}\) (inverse functions)

Under the assumptions of Theorem 2, let \(g\) be the inverse of \(f_{G}\left(f \text { restricted to } G=G_{\vec{p}}(\delta)\right)\).

Then \(g \in C D^{1}\) on \(f[G]\) and \(d g(\vec{y} ; \cdot)\) is the inverse of \(d f(\vec{x} ; \cdot)\) whenever \(\vec{x}=g(\vec{y}), \vec{x} \in G.\)

Briefly: "The differential of the inverse is the inverse of the differential."

Proof

Fix any \(\vec{y} \in f[G]\) and \(\vec{x}=g(\vec{y}) ;\) so \(\vec{y}=f(\vec{x})\) and \(\vec{x} \in G.\) Let \(U=d f(\vec{x} ; \cdot).\)

As noted above, \(U\) is bijective for every \(\vec{x} \in G\) by Theorems 1 and 2 in §6; so we may set \(V=U^{-1}.\) We must show that \(V=d g(\vec{y} ; \cdot).\)

To do this, give \(\vec{y}\) an arbitrary (variable) increment \(\Delta \vec{y},\) so small that \(\vec{y}+\Delta \vec{y}\) stays in \(f[G]\) (an open set by Theorem 2).

As \(g\) and \(f_{G}\) are one-to-one, \(\Delta \vec{y}\) uniquely determines

\[\Delta \vec{x}=g(\vec{y}+\Delta \vec{y})-g(\vec{y})=\vec{t},\]

and vice versa:

\[\Delta \vec{y}=f(\vec{x}+\vec{t})-f(\vec{x}).\]

Here \(\Delta \vec{y}\) and \(\vec{t}\) are the mutually corresponding increments of \(\vec{y}=f(\vec{x})\) and \(\vec{x}=g(\vec{y}).\) By continuity, \(\vec{y} \rightarrow \overrightarrow{0}\) iff \(\vec{t} \rightarrow \overrightarrow{0}.\)

As \(U=d f(\vec{x} ; \cdot)\),

\[\lim _{\vec{t} \rightarrow \overline{0}} \frac{1}{|\vec{t}|}|f(\vec{x}+\vec{t})-f(\vec{t})-U(\vec{t})|=0,\]

or

\[\lim _{\vec{t} \rightarrow \overrightarrow{0}} \frac{1}{|\vec{t}|}|F(\vec{t})|=0,\]

where

\[F(\vec{t})=f(\vec{x}+\vec{t})-f(\vec{t})-U(\vec{t}).\]

As \(V=U^{-1},\) we have

\[V(U(\vec{t}))=\vec{t}=g(\vec{y}+\Delta \vec{y})-g(\vec{y}).\]

So from (9),

\[\begin{aligned} V(F(\vec{t})) &=V(\Delta \vec{y})-\vec{t} \\ &=V(\Delta \vec{y})-[g(\vec{y}+\Delta \vec{y})-g(\vec{y})]; \end{aligned}\]

that is,

\[\frac{1}{|\Delta \vec{y}|}|g(\vec{y}+\Delta \vec{y})-g(\vec{y})-V(\Delta \vec{y})|=\frac{|V(F(\vec{t}))|}{|\Delta \vec{y}|}, \quad \Delta \vec{y} \neq \overrightarrow{0}.\]

Now, formula (4), with \(\vec{r}=\vec{x}, \vec{s}=\vec{x}+\vec{t},\) and \(\vec{u}=\vec{t},\) shows that

\[|f(\vec{x}+\vec{t})-f(\vec{x})| \geq \frac{1}{2} \varepsilon|\vec{t}|;\]

i.e., \(|\Delta \vec{y}| \geq \frac{1}{2} \varepsilon|\vec{t}|.\) Hence by (8),

\[\frac{|V(F(\vec{t}))|}{|\Delta \vec{y}|} \leq \frac{|V(F(\vec{t}) |}{\frac{1}{2} \varepsilon|\vec{t}|}=\frac{2}{\varepsilon}\left|V\left(\frac{1}{|\vec{t}|} F(\vec{t})\right)\right| \leq \frac{2}{\varepsilon}\|V\| \frac{1}{|\vec{t}|}|F(\vec{t})| \rightarrow 0 \text { as } \vec{t} \rightarrow \overrightarrow{0}.\]

Since \(\vec{t} \rightarrow \overrightarrow{0}\) as \(\Delta \vec{y} \rightarrow \overrightarrow{0}\) (change of variables!), the expression (10) tends to 0 as \(\Delta \vec{y} \rightarrow \overrightarrow{0}.\)

By definition, then, \(g\) is differentiable at \(\vec{y},\) with \(d g(\vec{y};)=V=U^{-1}\).

Moreover, Corollary 3 in §6, applies here. Thus

\[\left(\forall \delta^{\prime}>0\right)\left(\exists \delta^{\prime \prime}>0\right) \quad\|U-W\|<\delta^{\prime \prime} \Rightarrow\left\|U^{-1}-W^{-1}\right\|<\delta^{\prime}.\]

Taking here \(U^{-1}=d g(\vec{y})\) and \(W^{-1}=d g(\vec{y}+\Delta \vec{y}),\) we see that \(g \in C D^{1}\) near \(\vec{y}.\) This completes the proof.\(\quad \square\)

Note 2. If \(E^{\prime}=E=E^{n}\left(C^{n}\right),\) the bijectivity of \(\phi=d f(\vec{p} ; \cdot)\) is equivalent to

\[\operatorname{det}[\phi]=\operatorname{det}\left[f^{\prime}(\vec{p})\right] \neq 0\]

(Theorem 1 of §6).

In this case, the fact that \(f\) is one-to-one on \(G=G_{\vec{p}}(\delta)\) means, componentwise (see Note 3 in §6), that the system of \(n\) equations

\[f_{i}(\vec{x})=f\left(x_{1}, \ldots, x_{n}\right)=y_{i}, \quad i=1, \ldots, n,\]

has a unique solution for the \(n\) unknowns \(x_{k}\) as long as

\[\left(y_{1}, \ldots, y_{n}\right)=\vec{y} \in f[G].\]

Theorem 3 shows that this solution has the form

\[x_{k}=g_{k}(\vec{y}), \quad k=1, \ldots, n,\]

where the \(g_{k}\) are of class \(C D^{1}\) on \(f[G]\) provided the \(f_{i}\) are of class \(C D^{1}\) near \(\vec{p}\) and det \(\left[f^{\prime}(\vec{p})\right] \neq 0.\) Here

\[\operatorname{det}\left[f^{\prime}(\vec{p})\right]=J_{f}(\vec{p}),\]

as in §6.

Thus again \(f\) "locally" resembles a linear map, \(\phi=d f(\vec{p} ; \cdot)\).

IV. The Implicit Function Theorem. Generalizing, we now ask, what about solving \(n\) equations in \(n+m\) unknowns \(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}?\) Say, we want to solve

\[f_{k}\left(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}\right)=0, \quad k=1,2, \ldots, n,\]

for the first \(n\) unknowns (or variables) \(x_{k},\) thus expressing them as

\[x_{k}=H_{k}\left(y_{1}, \ldots, y_{m}\right), \quad k=1, \ldots, n,\]

with \(H_{k} : E^{m} \rightarrow E^{1}\) or \(H_{k} : C^{m} \rightarrow C\).

Let us set \(\vec{x}=\left(x_{1}, \ldots, x_{n}\right), \vec{y}=\left(y_{1}, \ldots, y_{m}\right),\) and

\[(\vec{x}, \vec{y})=\left(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}\right)\]

so that \((\vec{x}, \vec{y}) \in E^{n+m}\left(C^{n+m}\right)\).

Thus the system of equations (11) simplifies to

\[f_{k}(\vec{x}, \vec{y})=0, \quad k=1, \ldots, n\]

or

\[f(\vec{x}, \vec{y})=\overrightarrow{0},\]

where \(f=\left(f_{1}, \ldots, f_{n}\right)\) is a map of \(E^{n+m}\left(C^{n+m}\right)\) into \(E^{n}\left(C^{n}\right) ; f\) is a function of \(n+m\) variables, but it has \(n\) components \(f_{k};\) i.e.,

\[f(\vec{x}, \vec{y})=f\left(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}\right)\]

is a vector in \(E^{n}\left(C^{n}\right)\).

Theorem \(\PageIndex{4}\) (implicit functions)

Let \(E^{\prime}=E^{n+m}\left(C^{n+m}\right), E=E^{n}\left(C^{n}\right),\) and let \(f : E^{\prime} \rightarrow E\) be of class \(C D^{1}\) near

\[(\vec{p}, \vec{q})=\left(p_{1}, \ldots, p_{n}, q_{1}, \ldots, q_{m}\right), \quad \vec{p} \in E^{n}\left(C^{n}\right), \vec{q} \in E^{m}\left(C^{m}\right).\]

Let \([\phi]\) be the \(n \times n\) matrix

\[\left(D_{j} f_{k}(\vec{p}, \vec{q})\right), \quad j, k=1, \ldots, n.\]

If \(\operatorname{det}[\phi] \neq 0\) and if \(f(\vec{p}, \vec{q})=\overrightarrow{0},\) then there are open sets

\[P \subseteq E^{n}\left(C^{n}\right) \text { and } Q \subseteq E^{m}\left(C^{m}\right),\]

with \(\vec{p} \in P\) and \(\vec{q} \in Q,\) for which there is a unique map

\[H : Q \rightarrow P\]

with

\[f(H(\vec{y}), \vec{y})=\overrightarrow{0}\]

for all \(\vec{y} \in Q;\) furthermore, \(H \in C D^{1}\) on \(Q\).

Thus \(\vec{x}=H(\vec{y})\) is a solution of (11) in vector form.

Proof

With the above notation, set

\[F(\vec{x}, \vec{y})=(f(\vec{x}, \vec{y}), \vec{y}), \quad F : E^{\prime} \rightarrow E^{\prime}.\]

Then

\[F(\vec{p}, \vec{q})=(f(\vec{p}, \vec{q}), \vec{q})=(\overrightarrow{0}, \vec{q}),\]

since \(f(\vec{p}, \vec{q})=\overrightarrow{0}\).

As \(f \in C D^{1}\) near \((\vec{p}, \vec{q}),\) so is \(F\) (verify componentwise via Problem 9(ii) in §3 and Definition 1 of §5).

By Theorem 4, §3, \(\operatorname{det}\left[F^{\prime}(\vec{p}, \vec{q})\right]=\operatorname{det}[\phi] \neq 0\) (explain!).

Thus Theorem 1 above shows that \(F\) is one-to-one on some globe \(G\) about \((\vec{p}, \vec{q}).\)

Clearly \(G\) contains an open interval about \((\vec{p}, \vec{q}).\) We denote it by \(P \times Q\) where \(\vec{p} \in P, \vec{q} \in Q ; P\) is open in \(E^{n}\left(C^{n}\right)\) and \(Q\) is open in \(E^{m}\left(C^{m}\right).\)

By Theorem 3, \(F_{P \times Q}\) (\(F\) restricted to \(P \times Q)\) has an inverse

\[g : A \underset{\text { onto }}{\longleftrightarrow} P \times Q,\]

where \(A=F[P \times Q]\) is open in \(E^{\prime}\) (Theorem 2), and \(g \in C D^{1}\) on \(A.\) Let the map \(u=\left(g_{1}, \ldots, g_{n}\right)\) comprise the first \(n\) components of \(g\) (exactly as \(f\) comprises the first \(n\) components of \(F )\).

Then

\[g(\vec{x}, \vec{y})=(u(\vec{x}, \vec{y}), \vec{y})\]

exactly as \(F(\vec{x}, \vec{y})=(f(\vec{x}, \vec{y}), \vec{y}).\) Also, \(u : A \rightarrow P\) is of class \(C D^{1}\) on \(A,\) as \(g\) is (explain!).

Now set

\[H(\vec{y})=u(\overrightarrow{0}, \vec{y});\]

here \(\vec{y} \in Q,\) while

\[(\overrightarrow{0}, \vec{y}) \in A=F[P \times Q],\]

for \(F\) preserves \(\vec{y}\) (the last \(m\) coordinates). Also set

\[\alpha(\vec{x}, \vec{y})=\vec{x}.\]

Then \(f=\alpha \circ F\) (why?), and

\[f(H(\vec{y}), \vec{y})=f(u(\overrightarrow{0}, \vec{y}), \vec{y})=f(g(\overrightarrow{0}, \vec{y}))=\alpha(F(g(\overrightarrow{0}, \vec{y}))=\alpha(\overrightarrow{0}, \vec{y})=\overrightarrow{0}\]

by our choice of \(\alpha\) and \(g\) (inverse to \(F).\) Thus

\[f(H(\vec{y}), \vec{y})=\overrightarrow{0}, \quad \vec{y} \in Q,\]

as desired.

Moreover, as \(H(\vec{y})=u(\overrightarrow{0}, \vec{y}),\) we have

\[\frac{\partial}{\partial y_{i}} H(\vec{y})=\frac{\partial}{\partial y_{i}} u(\overrightarrow{0}, \vec{y}), \quad \vec{y} \in Q, i \leq m.\]

As \(u \in C D^{1},\) all \(\partial u / \partial y_{i}\) are continuous (Definition 1 in §5); hence so are the \(\partial H / \partial y_{i}.\) Thus by Theorem 3 in §3, \(H \in C D^{1}\) on \(Q.\)

Finally, \(H\) is unique for the given \(P, Q;\) for

\[\begin{aligned} f(\vec{x}, \vec{y})=\overrightarrow{0} & \Longrightarrow(f(\vec{x}, \vec{y}), \vec{y})=(\overrightarrow{0}, \vec{y}) \\ & \Longrightarrow F(\vec{x}, \vec{y})=(\overrightarrow{0}, \vec{y}) \\ & \Longrightarrow g(F(\vec{x}, \vec{y}))=g(\overrightarrow{0}, \vec{y}) \\ & \Longrightarrow(\vec{x}, \vec{y})=g(\overrightarrow{0}, \vec{y})=(u(\overrightarrow{0}, \vec{y}), \vec{y}) \\ & \Longrightarrow \vec{x}=u(\overrightarrow{0}, \vec{y})=H(\vec{y}). \end{aligned}\]

Thus \(f(\vec{x}, \vec{y})=\overrightarrow{0}\) implies \(\vec{x}=H(\vec{y});\) so \(H(\vec{y})\) is the only solution for \(\vec{x}. \quad \square\)

Note 3. \(H\) is said to be implicitly defined by the equation \(f(\vec{x}, \vec{y})=\overrightarrow{0}.\) In this sense we say that \(H(\vec{y})\) is an implicit function, given by \(f(\vec{x}, \vec{y})=\overrightarrow{0}\).

Similarly, under suitable assumptions, \(f(\vec{x}, \vec{y})=\overrightarrow{0}\) defines \(\vec{y}\) as a function of \(\vec{x}.\)

Note 4. While \(H\) is unique for a given neighborhood \(P \times Q\) of \((\vec{p}, \vec{q}),\) another implicit function may result if \(P \times Q\) or \((\vec{p}, \vec{q})\) is changed.

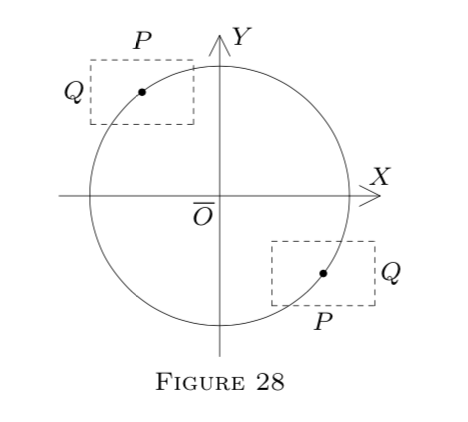
For example, let

\[f(x, y)=x^{2}+y^{2}-25\]

(a polynomial; hence \(f \in C D^{1}\) on all of \(E^{2}).\) Geometrically, \(x^{2}+y^{2}-25=0\) describes a circle.

Solving for \(x,\) we get \(x=\pm \sqrt{25-y^{2}}.\) Thus we have two functions:

\[H_{1}(y)=+\sqrt{25-y^{2}}\]

and

\[H_{2}(y)=-\sqrt{25-y^{2}}.\]

If \(P \times Q\) is in the upper part of the circle, the resulting function is \(H_{1}.\) Otherwise, it is \(H_{2}.\) See Figure 28.

V. Implicit Differentiation. Theorem 4 only states the existence (and uniqueness) of a solution, but does not show how to find it, in general.

The knowledge itself that \(H \in C D^{1}\) exists, however, enables us to use its derivative or partials and compute it by implicit differentiation, known from calculus.

Examples

(a) Let \(f(x, y)=x^{2}+y^{2}-25=0,\) as above.

This time treating \(y\) as an implicit function of \(x, y=H(x),\) and writing \(y^{\prime}\) for \(H^{\prime}(x),\) we differentiate both sides of (x^{2}+y^{2}-25=0\) with respect to \(x,\) using the chain rule for the term \(y^{2}=[H(x)]^{2}\).

This yields \(2 x+2 y y^{\prime}=0,\) whence \(y^{\prime}=-x / y\).

Actually (see Note 4), two functions are involved: \(y=\pm \sqrt{25-x^{2}};\) but both satisfy \(x^{2}+y^{2}-25=0;\) so the result \(y^{\prime}=-x / y\) applies to both.

Of course, this method is possible only if the derivative \(y^{\prime}\) is known to exist. This is why Theorem 4 is important.

(b) Let

\[f(x, y, z)=x^{2}+y^{2}+z^{2}-1=0, \quad x, y, z \in E^{1}.\]

Again \(f\) satisfies Theorem 4 for suitable \(x, y,\) and \(z\).

Setting \(z=H(x, y),\) differentiate the equation \(f(x, y, z)=0\) partially with respect to \(x\) and \(y.\) From the resulting two equations, obtain \(\frac{\partial z}{\partial x}\) and \(\frac{\partial z}{\partial y}\).