1.5: Roots of Complex Numbers

Recall that if $z=x+iy$ is a nonzero complex number, then it can be written in polar form as

$z=r(cosθ+isinθ)$

where $r=\sqrt{x^{2}+y^{2}}$ and $\theta$ is the angle, in radians, from the positive x-axis to the ray connecting the origin to the point $z$.

Now, de Moivre’s formula establishes that if $z=r(cosθ+isinθ)$ and $n$ is a positive integer, then

$z^{n}=r^{n}(cosn\theta +isinn\theta )$

Let $w$ be a complex number. Using de Moivre’s formula will help us to solve the equation

$z^{n}=w$

for $z$ when $w$ is given.

Suppose that $w=r(cosθ+isinθ)$ and $z=\rho(cos\psi +isin\psi )$ Then de Moivre’s formula gives

$z^{n}=\rho ^{n}(cosn\psi +isinn\psi )$

It follows that

$\rho ^{n}=r=\left | w \right |$

by uniqueness of the polar representation and

$n\Psi =\theta +k(2\pi )$,

where $k$ is some integer. Thus

$z=\sqrt[n]{r}[cos(\frac{\theta }{n}+\frac{2k\pi }{n})+isin(\frac{\theta }{n}+\frac{2k\pi }{n})]$.

Each value of $k=0,1,2,…,n−1$ gives a different value of $z$. Any other value of $k$ merely repeats one of the values of $z$ corresponding to $k=0,1,2,…,n−1$. Thus there are exactly $n$th roots of a nonzero complex number.

Using Euler’s formula:

$e^{i\theta }=cos\theta +isin\theta$,

the complex number \(z=r(cos\theta +isin\theta) \\) can also be written in exponential form as

$z=re^{i\theta }$

Thus, the $n$th roots of a nonzero complex number $z≠0$ can also be expressed as

$\begin{eqnarray}\label{expform} z=\sqrt[n]{r}\;\mbox{exp}\left[i\left(\frac{\theta}{n}+\frac{2k\pi}{n}\right)\right] \end{eqnarray}$

where $k=0,1,2,...,n-1$.

The applet below shows a geometrical representation of the $n$th roots of a complex number, up to $n=10$. Drag the red point around to change the value of $z$ or drag the sliders.

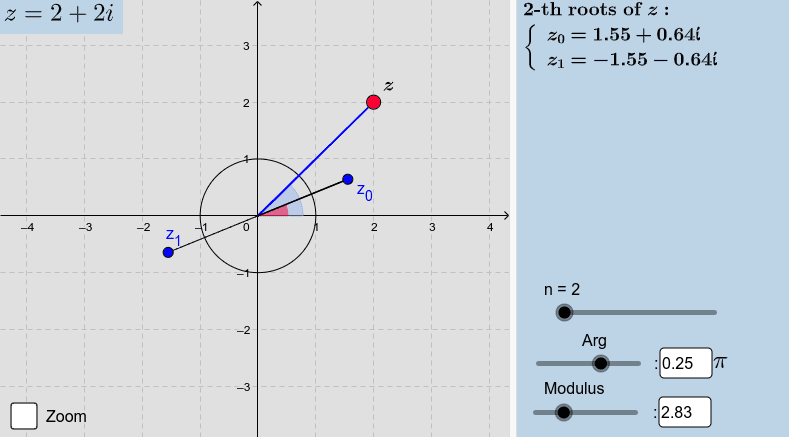
Code

Enter the following script in GeoGebra to explore it yourself and make your own version. The symbol # indicates comments.

#Complex number
    
Z = 1 + ί

#Modulus of Z

r = abs(Z)

#Angle of Z

theta = atan2(y(Z), x(Z))

#Number of roots

n = Slider(2, 10, 1, 1, 150, false, true, false, false)

#Plot n-roots

nRoots = Sequence(r^(1 / n) * exp(  ί * ( theta / n + 2 * pi * k / n ) ), k, 0, n-1)

---

Exercise $\PageIndex{1}$

From the exponential form (1) of the roots, show that all the $n$th roots lie on the circle $\left | z \right |=\sqrt[n]{r}$ about the origin and are equally spaced every $\frac{2\pi }{n}$ radians, starting with argument $\frac{\theta }{n}$.