1.6: Topology of the Complex Plane

Neighbourhoods

An \(ε\) neighbourhood, also called open ball or open disk, of a complex number \(z_{0}\) consists of all points \(z\) lying inside but not on a circle centred at \(z_{0}\) and with radius \(ε>0\) and is expressed by

\(\begin{eqnarray}
                B_{\varepsilon}(z_0)=\{z:|z-z_0| \lt \varepsilon\}
                \end{eqnarray}\)

The closed  \(ε\) neighbourhood of \(z_{0}\) is expressed by

\(\begin{eqnarray}
                \overline{B}_{\varepsilon}(z_0)=\{z:|z-z_0|\leq \varepsilon\}
                \end{eqnarray}\)

And finally, a deleted \(ε\) neighbourhood of \(z_{0}\), also called punctured balls or disks, is expressed by

\(\begin{eqnarray}
                B_{\varepsilon}(z_0)\setminus \{z_0\}=\{z:0 \lt |z-z_0| \lt \varepsilon\}
                \end{eqnarray}\)

Figure 1 shows the geometrical representation of the following examples:

1. \(B_{1}(0)=\left \{z:|z|<1\right \}\)
2. \(\bar{B}_{\frac{7}{8}}(-1-\sqrt{2}i)=\left \{ z:\left | z-(-1-\sqrt{2}i) \right |\leq \frac{7}{8} \right \}\)
3. \(\bar{B}_{\frac{1}{2}}(2+\sqrt{3}i)\setminus \left \{ 2+\sqrt{3}i \right \}=\left \{ z:0< \left | z-(2+\sqrt{3}i) \right |\leq \frac{1}{2} \right \}\)

Figure 1: Geometrical representation of neighbourhoods.

---

Classification of points

A point \(z_{0}\) is said to be an interior point of a set \(S\subset \mathbb{C}\) whenever there is some neighbourhood of \(z_{0}\) that contains only points of \(S\); it is called an exterior point of \(S\) when there exists a neighbourhood of it containing no points of \(S\). If \(z_{0}\) is neither of these, it is a boundary point of \(S\). A boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in \(S\) and at least one point not in \(S\). The totality of all boundary points is called the boundary of \(S\).

In this text we will use the following notation:

1. Int \(S=\left \{ z:z \,is \,an\,interior\,point\,of \,S \right \}\)
2. Ext \(S=\left \{ z:z \,is \,an\,exterior\,point\,of \,S \right \}\)
3. \(\partial S=\left \{ z:z \,is \,a\,boundary\,point\,of \,S \right \}\)

Figure 2: Interior, boundary, and exterior of set S.

Considering the previous examples of neighbourhoods, let

\(S_{1}=B_{1}(0)\), \(S_{2}=\bar{B}_{\frac{7}{8}}(-1-\sqrt{2}i)\) and \(S_{3}=\bar{B}_{\frac{1}{2}}(2+\sqrt{3}i)\setminus \left \{ 2+\sqrt{3}i \right \}\).

Thus, for \(S_{1}\) we have:

• Int \(S_{1}=B_{1}(0)\)
• Ext \(S_{1}=\left \{ z:\left | z \right |> 1 \right \}\)
• \(\partial S_{1}=\left \{ z:\left | z \right |= 1 \right \}\)

For \(S_{2}\) we have:

• Int \(S_{2}=B_{\frac{7}{8}}(-1-\sqrt{2})\)
• Ext \(S_{2}=\left \{ z:\left | z-(-1-\sqrt{2}i) \right |>\frac{7}{8} \right \}\)
• \(\partial S_{2}=\left \{ z:\left | z-(-1-\sqrt{2}i) \right |=\frac{7}{8} \right \}\)

And finally, for \(S_{3}\) we have:

• Int \( S_{3}=B_{\frac{1}{2}}(2+\sqrt{3})\)
• Ext \(S_{3}=\left \{ z:\left | z-(2+\sqrt{3}i) \right |>\frac{1}{2} \right \}\)
• \(\partial S_{3}=\left \{ z:\left | z-(2+\sqrt{3}i) \right |=\frac{1}{2} \right \}\cup \left \{ 0 \right \}\)

---

Topological space

A set \(S\) is open if for every \(z\in S\), exits \(\varepsilon > 0\) such that

\(B_{\varepsilon }(z)\subset S\).

That is, Int \(S=S\). A set \(S\) is closed if it contains all of its boundary points, that is

\(\partial S\subseteq S\).

The set \(\mathbb{C}\) is both open and closed since it has no boundary points.

The set \(\mathbb{C}\), together with the collection \(\tau =\left \{ S\subseteq \mathbb{C}:S \,is \,open \right \}\) is a topological space, and this is expressed by the pair \(\left ( \mathbb{C},\tau  \right )\). The topological space \(\left ( \mathbb{C},\tau  \right )\) satisfies the following:

1. \(\varnothing \) and \(\mathbb{C}\) are open.
2. Whenever two or more sets are open, then so is their union.
3. Whenever sets \(S_{1}\) and \(S_{2}\) are open, then so is \(S_{1}\cap S_{2}\).

 

Remark: The technical definition of topological space is a bit unintuitive, particularly if you haven’t studied topology. In essence, it states that the geometric properties of subsets of \(\mathbb{C}\) will be preserved when continuous transformations (functions or mappings) are applied.

The closure of a set \(S\) is the closed set consisting of all points in \(S\) together with the boundary of \(S\). In other words

\(\bar{S}=S\cup \partial S\).

An open set \(S\) is connected if each pair of points \(z_{1}\) and \(z_{2}\) in it can be joined by a polygonal line, consisting of a finite number of line segments joined end to end, that lies entirely in \(S\).

Figure 3: Connected set.

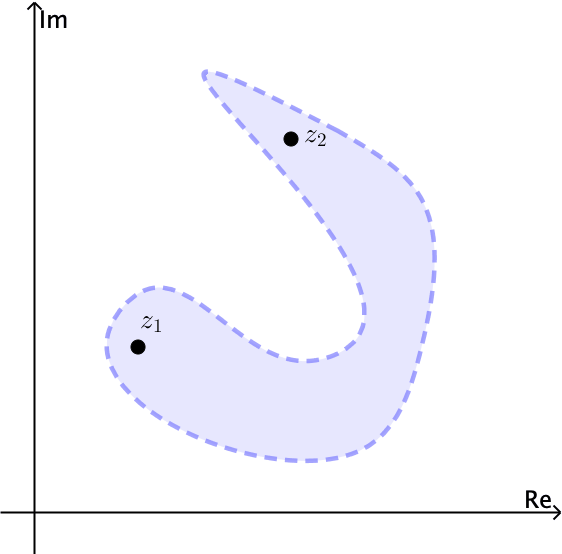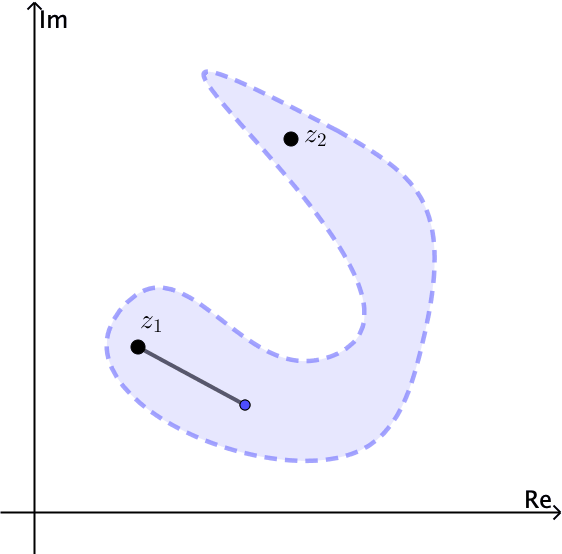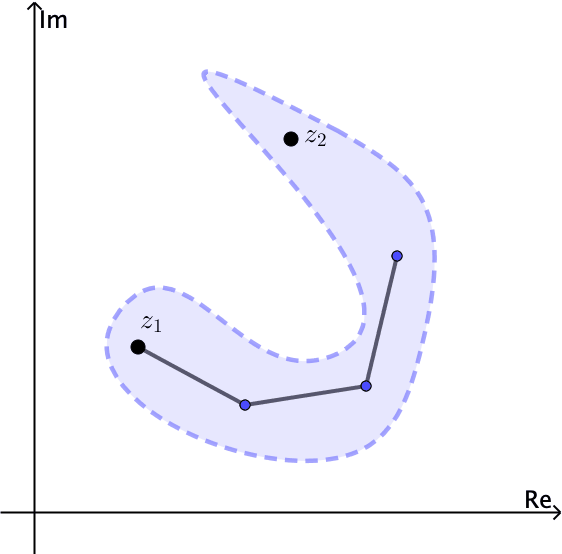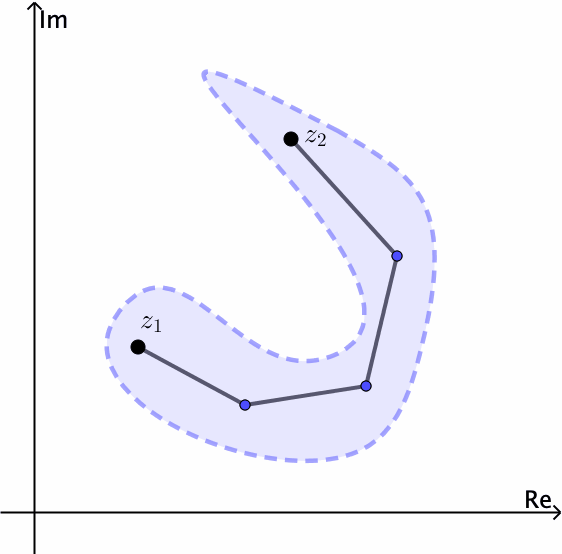
Notice for example that the open set \(\left | z \right |< 1\) is connected. The annulus \(1< \left | z \right |<2\) is open and also connected, see Figures 4 and 5.

Figure 4: \(\left | z \right |< 1\) 

Figure 5: \(\left | z \right |<2\)

A nonempty open set that is connected is called a domain. In this context, any neighbourhood is a domain. A domain together with some, none, or all of its boundary points is referred to as a region. In other words, a set whose interior is a domain is called a region. A set \(S\) is bounded if there is \(R>0\) such that

\(S\subset B_{R}(0)=\left \{ z\in \mathbb{C}:\left | z \right |<R \right \}\).

Figure 6: Bounded set.

Exercise \(\PageIndex{1}\)

Sketch the set \(S\) of points in the complex plane satisfying the given inequality. Determine whether the set is (a) open, (b) closed, (c) a domain, (d) bounded, or (e) connected.

• \(Im(z)<0\)
• \(−1<Re(z)<1\)
• \(|z|>1|z|>1\)
• \(2≤|z−3+4i|≤5\)