6.4: Joukowsky Airfoil

The Joukowsky map

A well known example of a conformal function is the Joukowsky map

\(\begin{eqnarray}\label{jouk}
        w= z+ 1/z.
    \end{eqnarray}\)

It was first used in the study of flow around airplane wings by the pioneering Russian aero and hydrodynamics researcher Nikolai Zhukovskii (Joukowsky).

Since

\(\frac{d}{dz}w=1-\frac{1}{z^2}=0\quad \text{if and only if}\quad z=\pm 1,\)

the function (1) is conformal except at the critical points \(z=±1\) as well as the singularity \(z=0\), where it is not defined.

If \(z = e^{i\theta}\) lies on the unit circle, then

\(w =e^{i\theta}+e^{-i\theta}=2\cos \theta,\)

lies on the real axis, with \(-2\leq w\leq  2\). Thus, the Joukowsky map squashes the unit circle down to the real line segment \([−2,2]\). The images of points outside the unit circle fill the rest of the \(w\) plane, as do the images of the (nonzero) points inside the unit circle. Indeed, if we solve (1) for \(z\), we have

\(z=\frac{1}{2}\left(w\pm \sqrt{w^2-4}\right).\)

We see that every \(w\) except \(±2\) comes from two different points \(z\); for \(w\) not on the critical line segment \([−2,2]\), one point (with the minus sign) lies inside and one (with the plus sign) lies outside the unit circle, whereas if \(−2<w<2\), both points lie on the unit circle and a common vertical line.

Therefore, the Joukowski map defines a one-to-one conformal mapping from \(|z|>1\), the exterior of the unit circle, onto the exterior of the line segment \([−2,2]\), i. e. \(\mathbb C \setminus [-2, 2]\)

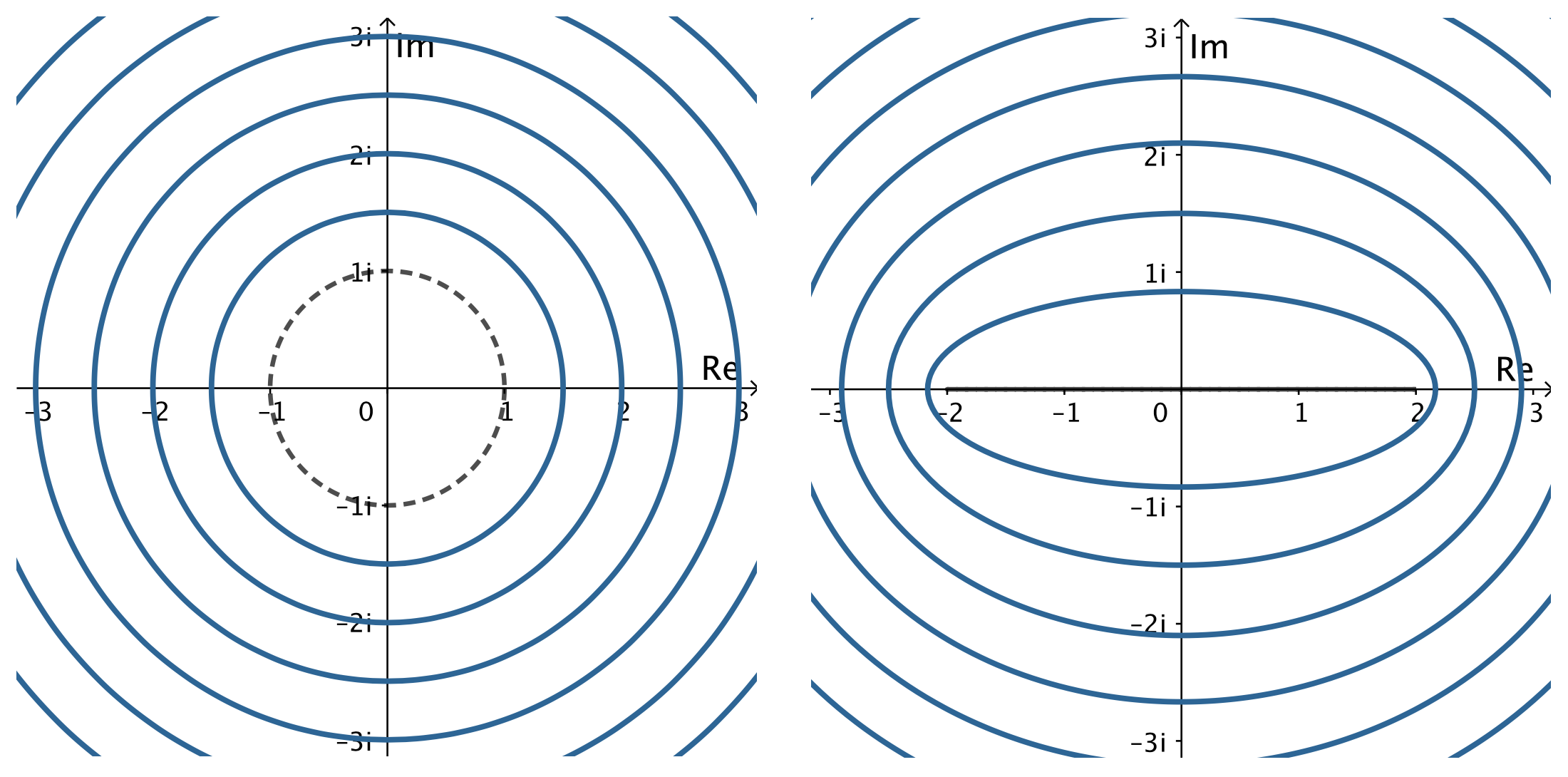
In Figure 4 we can observe that the concentric circles \(|z|=r>1\) are mapped to ellipses with foci at \(±2\) in the \(w\)-plane.

Figure 4: The Joukowsky map applied to \(|z|=r \geq 1\).

The effect on circles not centered at the origin is more interesting. The image curves take in a wide variety of shapes. When the circle passes through the singular point \(z=1\), then its image is no longer smooth, but has a cusp at \(w=2\) and when the circle passes through \(z=−1\) the cusp is at \(w=−2\). Some of the image curves assume the shape of the famous cross-section through an idealized airplane wing or airfoil, also known as the Joukowsky airfoil.

You can explore the Joukowsky map in the applet below. Drag around the center of the circle. Drag sliders to apply the mapping or change the radius. Click button to see predefined values.

---

Flow around the Joukowsky airfoil

Consider now the uniform flow around the unit circle with circulation \(C\) and speed \(U>0\) given by the complex potential

\(\begin{eqnarray}\label{eq1}
            F(z)=Uz+\frac{U}{z}-\frac{i C}{2\pi}\log z.
            \end{eqnarray}\)

We can use the linear transformation

\(T(z)=-0.15+0.23i + 0.23\sqrt{13\cdot 2} z\)

to map this flow around \(|z|=1\) onto the flow around the circle \(c_1\) with center \(z_1=−0.15+0.23i\) and radius \(r=0.23\sqrt{13\cdot 2}\)

Finally, by applying the Joukowsky map (1), we can obtain a uniform flow with circulation around the Joukowsky airfoil.

The following simulation shows the uniform flow past the circular cylinder \(c_1\) and its transformation to the Joukowsky airfoil. Drag the sliders to explore:

• Slider \(U\) = speed.
• Slider \(C\) = circulation.
• Slider \(T\) = apply transformation.

Press the Trace button to show streamlines.

Reset