5.3: Proof of Cauchy's integral formula

Useful theorem

Before proving the theorem we’ll need a theorem that will be useful in its own right.

Theorem $\PageIndex{1}$: A second extension of Cauchy's theorem

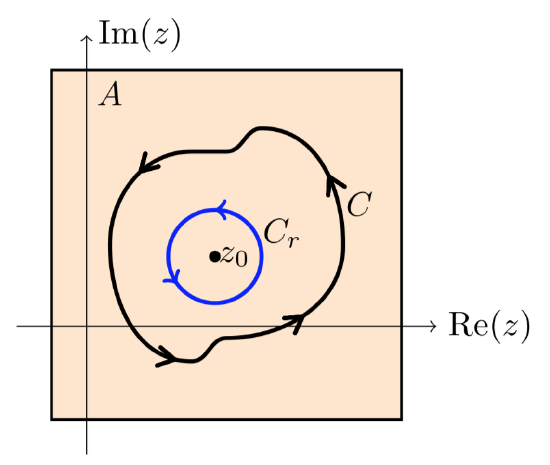
Suppose that $A$ is a simply connected region containing the point $z_0$. Suppose $g$ is a function which is

1. Analytic on $A$ - {$z_0$}
2. Continuous on $A$. (In particular, $g$ does not below up at $z_0$.)

Then

$$\int_{C} g(z)\ dz = 0 \nonumber$$

for all closed curves $C$ in $A$.

Proof

The extended version of Cauchy’s theorem in the Topic 3 notes tells us that

$$\int_C g(z)\ dz = \int_{C_r} g(z)\ dz, \nonumber$$

where $C_r$ is a circle of radius $r$ around $z_0$.

Since $g(z)$ is continuous we know that $|g(z)|$ is bounded inside $C_r$. Say, $|g(z)| < M$. The corollary to the triangle inequality says that

$$|\int_{C_r} g(z)\ dz| \le M \text{ (length of } C_r) = M2 \pi r. \nonumber$$

Since $r$ can be as small as we want, this implies that

$$\int_{C_r} g(z) \ dz = 0. \nonumber$$

Note

Using this, we can show that $g(z)$ is, in fact, analytic at $z_0$. The proof will be the same as in our proof of Cauchy’s theorem that $g(z)$ has an antiderivative.

Proof of Cauchy’s integral formula

We reiterate Cauchy’s integral formula from Equation 5.2.1: $f(z_0) = \dfrac{1}{2\pi i} \int_C \dfrac{f(z)}{z - z_0} \ dz$.

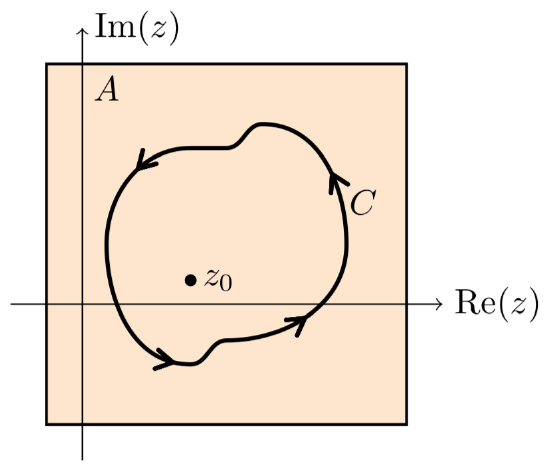
$Proof$. (of Cauchy’s integral formula) We use a trick that is useful enough to be worth remembering. Let

$$g(z) = \dfrac{f(z) - f(z_0)}{z - z_0}. \nonumber$$

Since $f(z)$ is analytic on $A$, we know that $g(z)$ is analytic on $A - \{z_0\}$. Since the derivative of $f$ exists at $z_0$, we know that

$$\lim_{z \to z_0} g(z) = f'(z_0). \nonumber$$

That is, if we define $g(z_0) = f'(z_0)$ then $g$ is continuous at $z_0$. From the extension of Cauchy's theorem just above, we have

$$\int_{C} g(z)\ dz = 0, \text{ i.e. } \int_C \dfrac{f(z) - f(z_0)}{z - z_0} \ dz = 0. \nonumber$$

Thus

$$\int_{C} \dfrac{f(z)}{z - z_0}\ dz = \int_C \dfrac{f(z_0)}{z - z_0}\ dz = f(z_0) \int_C \dfrac{1}{z - z_0} \ dz = 2\pi i f(z_0). \nonumber$$

The last equality follows from our, by now, well known integral of $1/(z - z_0)$ on a loop around $z_0$.