11.10: Solving the Dirichlet problem for harmonic functions
- Page ID
- 51144
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In general, a Dirichlet problem in a region \(A\) asks you to solve a partial differential equation in \(A\) where the values of the solution on the boundary of \(A\) are specificed.
Find a function \(u\) harmonic on the unit disk such that
\[u(e^{i \theta}) = \begin{cases} 1 & \text{ for } 0 < \theta < \pi \\ 0 & \text{ for } -\pi < \theta < 0 \end{cases} \nonumber \]
This is a Dirichlet problem because the values of \(u\) on the boundary are specified. The partial differential equation is implied by requiring that \(u\) be harmonic, i.e. we require \(\nabla ^2 u = 0\). We will solve this problem in due course.
Harmonic functions on the upper half-plane
Our strategy will be to solve the Dirichlet problem for harmonic functions on the upper half-plane and then transfer these solutions to other domains.
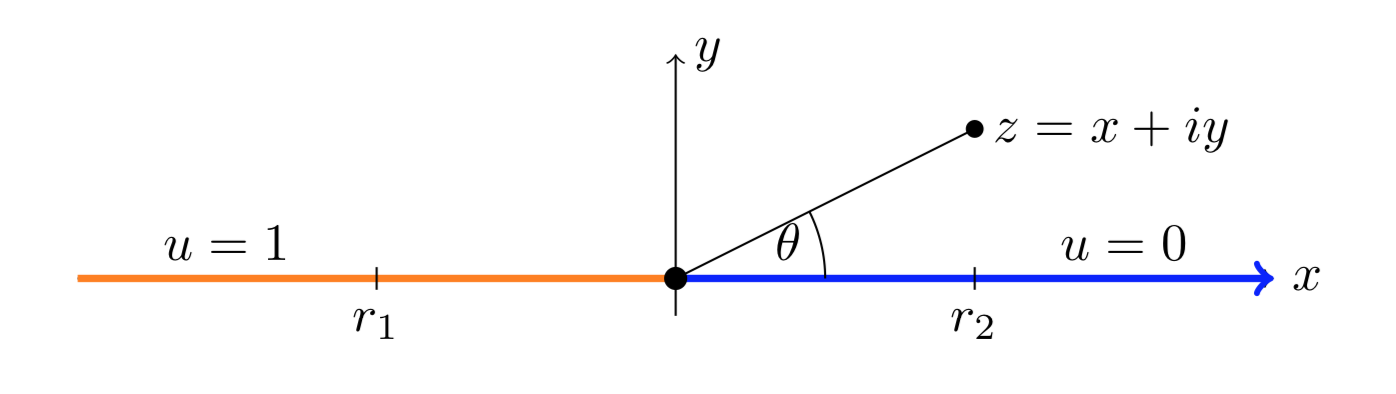
Find a harmonic function \(u(x, y)\) on the upper half-plane that satisfies the boundary condition
\[u(x, 0) = \begin{cases} 1 & \text{ for } x < 0 \\ 0 & \text{ for } x > 0 \end{cases} \nonumber \]
Solution
We can write down a solution explicitly as
\[u(x, y) = \dfrac{1}{\pi} \theta, \nonumber \]
where \(\theta\) is the argument of \(z = x + iy\). Since we are only working on the upper half-plane we can take any convenient branch with branch cut in the lower half-plane, say \(-\pi /2 < \theta < 3 \pi /2\).
To show \(u\) is truly a solution, we have to verify two things:
- \(u\) satisfies the boundary conditions
- \(u\) is harmonic.
Both of these are straightforward. First, look at the point \(r_2\) on the positive \(x\)-axis. This has argument \(\theta = 0\), so \(u(r_2, 0) = 0\). Likewise \(\text{arg} (r_1) = \pi\), so \(u(r_1, 0) = 1\). Thus, we have shown point (1).
To see point (2) remember that
\[\log (z) = \log (r) + i \theta. \nonumber \]
So,
\[u = \text{Re} (\dfrac{1}{\pi i} \log (z)). \nonumber \]
Since it is the real part of an analytic function, \(u\) is harmonic.
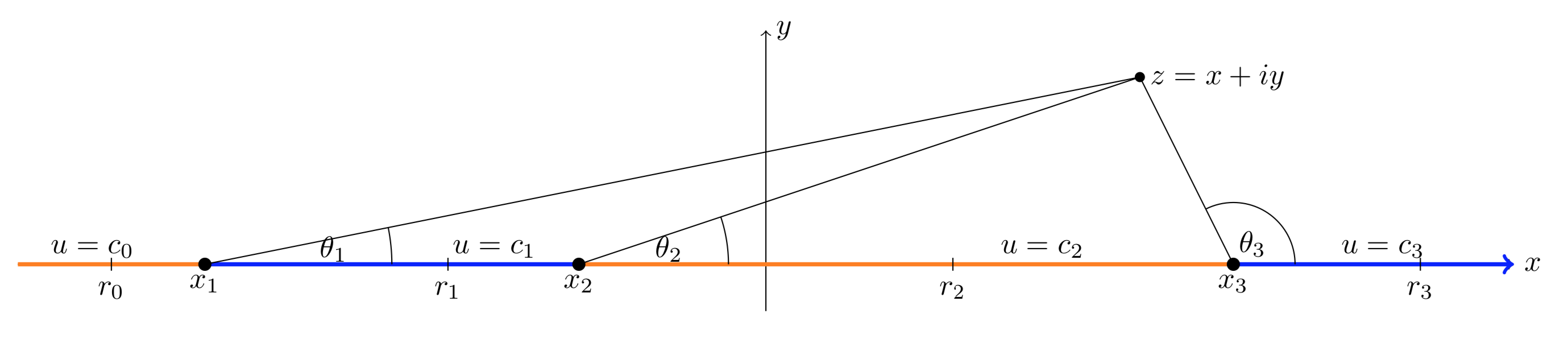
Suppose \(x_1 < x_2 < x_3\). Find a harmonic function \(u\) on the upper half-plane that satisfies the boundary condition
\[u(x, 0) = \begin{cases} c_0 & \text{ for } x < x_1 \\ c_1 & \text{ for } x_1 < x < x_2 \\ c_2 & \text{ for } x_2 < x < x_3 \\ c_3 & \text{ for } x_3 < x \end{cases} \nonumber \]
Solution
We mimic the previous example and write down the solution
\[u(x, y) = c_3 + (c_2 - c_3) \dfrac{\theta_3}{\pi} + (c_1 - c_2) \dfrac{\theta_2}{\pi} + (c_0 - c_1) \dfrac{\theta_1}{\pi}. \nonumber \]
Here, the \(\theta_j\) are the angles shown in the figure. One again, we chose a branch of \(\theta\) that has \(0 < \theta < \pi\) for points in the upper half-plane. (For example the branch \(-\pi /2 < \theta < 3\pi /2\).)
To convince yourself that \(u\) satisfies the boundary condition test a few points:
- At \(r_3\): all the \(\theta_j = 0\). So, \(u(r_3, 0) = c_3\) as required.
- At \(r_2\): \(\theta_1 = \theta_2 = 0\), \(\theta_3 = \pi\). So, \(u(r_2, 0) = c_3 + c_2 - c_3 = c_2\) as required.
- Likewise, at \(r_1\) and \(r_0\), \(u\) have the correct values.
As before, \(u\) is harmonic because it is the real part of the analytic function
\[\Phi (z) = c_3 + \dfrac{(c_2 - c_3)}{\pi i} \log (z - x_3) + \dfrac{(c_1 - c_2)}{\pi i} \log (z - x_2) + \dfrac{(c_1 - c_0)}{\pi i} \log (z - x_1). \nonumber \]
Harmonic functions on the unit disk
Let’s try to solve a problem similar to the one in Example 11.9.1..
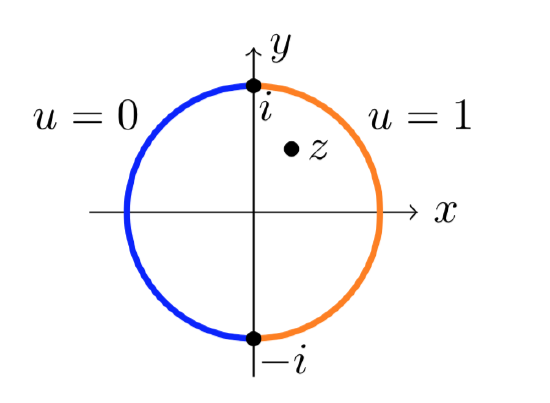
Find a function \(u\) harmonic on the unit disk such that
\[u (e^{i \theta}) = \begin{cases} 1 & \text{ for } -\pi /2 < \theta < \pi /2 \\ 0 & \text{ for } \pi /2 < \theta < 3\pi /2 \end{cases} \nonumber \]
Solution
Our strategy is to start with a conformal map \(T\) from the upper half-plane to the unit disk. We can use this map to pull the problem back to the upper half-plane. We solve it there and then push the solution back to the disk.
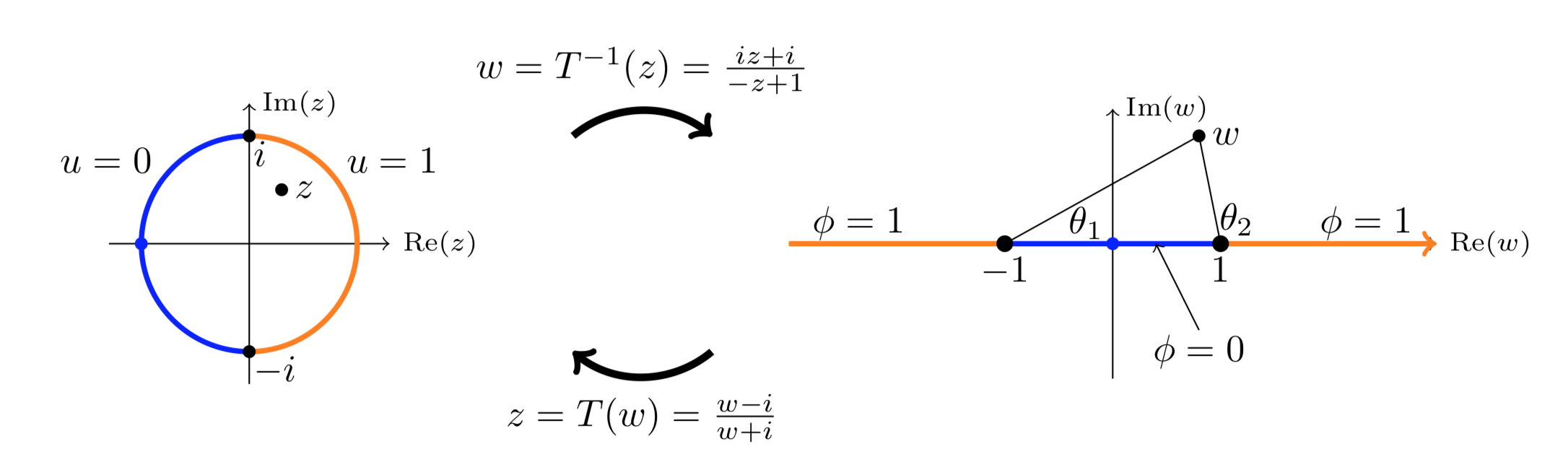
Let’s call the disk \(D\), the upper half-plane \(H\). Let \(z\) be the variable on \(D\) and \(w\) the variable on \(H\). Back in Example 11.7.4 we found a map from \(H\) to \(D\). The map and its inverse are
\[z = T(w) = \dfrac{w - i}{w + i}, \ \ \ \ \ \ \ \ w = T^{-1} (z) = \dfrac{iz + i}{-z + 1}. \nonumber \]
The function \(u\) on \(D\) is transformed by \(T\) to a function \(\phi\) on \(H\). The relationships are
\[u(z) = \phi \circ T^{-1} (z)\ \ \ \ \ \ \ \ \text{or} \ \ \ \ \ \ \ \ \phi (w) = u \circ T(w) \nonumber \]
These relationships determine the boundary values of \(\phi\) from those we were given for \(u\). We compute:
\(T^{-1} (i) = -1\), \(T^{-1} (-i) = 1\), \(T^{-1} (1) = \infty\), \(T^{-1} (-1) = 0\).
This shows the left hand semicircle bounding \(D\) is mapped to the segment [-1, 1] on the real axis. Likewise, the right hand semicircle maps to the two half-lines shown. (Literally, to the ‘segment’ 1 to \(\infty\) to -1.)
We know how to solve the problem for a harmonic function \(\phi\) on \(H\):
\[\phi (w) = 1 - \dfrac{1}{\pi} \theta _2 + \dfrac{1}{\pi} \theta _1 = \text{Re} (1 - \dfrac{1}{\pi i} \log (w - 1) + \dfrac{1}{\pi i} \log (w + 1)). \nonumber \]
Transforming this back to the disk we have
\[u(z) = \phi \circ T^{-1} (z) = \text{Re} (1 - \dfrac{1}{\pi i} \log (T^{-1} (z) - 1) + \dfrac{1}{\pi i} \log (T^{-1} (z) + 1)). \nonumber \]
If we wanted to, we could simplify this somewhat using the formula for \(T^{-1}\).


