3.4: Properties of Continuous Functions

Recall from Definition 2.6.3 that a subset $A$ of $\mathbb{R}$ is compact if and only if every sequence $\left\{a_{n}\right\}$ in $A$ has a subsequence $\left\{a_{n_{k}}\right\}$ that converges to a point $a \in A$.

Theorem $\PageIndex{1}$

Let $D$ be a nonempty compact subset of $\mathbb{R}$ and let $f: D \rightarrow \mathbb{R}$ be a continuous function. Then $f{D}$ is a compact subset of $\mathbb{R}$. In particular, $f(D)$ is closed and bounded.

Proof

Take any sequence $\left\{y_{n}\right\}$ in $f(D)$. Then for each $n$, there exists $a_{n} \in D$ such that $y_{n}=f\left(a_{n}\right)$. Since $D$ is compact, there exists a subsequence $\left\{a_{n_{k}}\right\}$ of $\left\{a_{n}\right\}$ and a point $a \in D$ such that

$$\lim _{k \rightarrow \infty} a_{n_{k}}=a \in D .$$

It now follows from Theorem 3.3.3 that

$$\lim _{k \rightarrow \infty} y_{n_{k}}=\lim _{k \rightarrow \infty} f\left(a_{n_{k}}\right)=f(a) \in f(D) .$$

Therefore, $f(D)$ is compact.

The final conclusion follows from Theorem 2.6.5 $\square$

Definitions $\PageIndex{1}$: Absolute Minimum and Absolute Maximum

We say that the function $f: D \rightarrow \mathbb{R}$ has an absolute minimum at $\bar{x} \in D$ if

$$f(x) \geq f(\bar{x}) \text { for every } x \in D.$$

Similarly, we say that $f$ has an absolute maximum at $\bar{x}$ if

$$f(x) \leq f(\bar{x}) \text { for every } x \in D.$$

Figure $3.2$: Absolute maximum and absolute minimum of $f$ on $[a, b]$.

Theorem $\PageIndex{2}$: Extreme Value Theorem

Suppose $f: D \rightarrow \mathbb{R}$ is continuous and $D$ is a compact set. Then $f$ has an absolute minimum and an asolute maximum on $D$.

Proof

Since $D$ is compact, $A=f(D)$ is closed and bounded (see Theorem 2.6.5). Let

$$m=\inf A=\inf _{x \in D} f(x).$$

In particular, $m \in \mathbb{R}$. For every $n \in \mathbb{N}$, there exists $a_{n} \in A$ such that

$$m \leq a_{n}<m+1 / n.$$

For each $n$, since $a_{n} \in A=f(D)$, there exists $x_{n} \in D$ such that $a_{n}=f\left(x_{n}\right)$ and, hence,

$$m \leq f\left(x_{n}\right)<m+1 / n.$$

By the compactness of $D$, there exists an element $\bar{x} \in D$ and a subsequence $\left\{x_{n_{k}}\right\}$ that converges to $\bar{x} \in D$ as $k \rightarrow \infty$. Because

$$m \leq f\left(x_{n_{k}}\right)<m+\frac{1}{n_{k}} \text { for every } k$$

by the squeeze theorem (Theorem 2.1.6) we conclude $\lim _{k \rightarrow \infty} f\left(x_{n_{k}}\right)=m$. On the other hand, by continuity we have $\lim _{k \rightarrow \infty} f\left(x_{n_{k}}\right)=f(\bar{x})$. We conclude that $f(\bar{x})=m \leq f(x)$ for every $x \in D$. Thus, $f$ has an absolute minimum at $\bar{x}$. The proof is similar for the case of absolute maximum. $\square$

Remark $\PageIndex{3}$

The proof of Theorem 3.4.2 can be shortened by applying Theorem 2.6.4. However, we have provided a direct proof instead.

Corollary $\PageIndex{4}$

If $f:[a, b] \rightarrow \mathbb{R}$ is continuous, then it has an absolute minimum and an absolute maximum on $[a, b]$.

Proof

Add proof here and it will automatically be hidden

Corollary 3.4.4 is sometimes referred to as the Extreme Value Theorem. It follows immediately from Theorem 3.4.2, and the fact that the interval $[a, b]$ is compact (see Example 2.6.4).

The following result is a basic property of continuous functions that is used in a variety of situations.

Lemma $\PageIndex{5}$

Let $f: D \rightarrow \mathbb{R}$ be continuous at $c \in D$. Suppose $f(c) > 0$. Then there exists $\delta > 0$ such that

$$f(x)>0 \text { for every } x \in B(c ; \delta) \cap D.$$

Proof

Let $\varepsilon=f(c)>0$. By the continuity of $f$ at $c$, ther exists $\delta > 0$ such that $x \in D$ and $|x-c|<\delta$, then

$|f(x)-f(c)|<\varepsilon$.

This implies, in particular, that $f(x)>f(c)-\varepsilon=0$ for every $x \in B(c ; \delta) \cap D$. The proof is now complete. $\square$

Remark $\PageIndex{6}$

An analogous result holds if $f(c)<0$.

Theorem $\PageIndex{7}$

Let $f:[a, b] \rightarrow \mathbb{R}$ be a continuous function. Suppose $f(a) \cdot f(b)<0$ (this means either $f(a)<0<f(b) \text { or } f(a)>0>f(b)$). Then there exists $c \in (a,b)$ such that $f(c)=0$.

Proof

We prove only the case $f(a)<0<f(b)$ (the case $f(a)>0>f(b)$ is completely analogous). Define

$$A=\{x \in[a, b]: f(x) \leq 0\} .$$

This set is nonempty since $a \in A$. This set is also bounded since $A \subset[a, b]$. Therefore, $c=\sup A$ exists and $a \leq c \leq b$. We are going to prove that $f(c)=0$ by showing that $f(c)<0$ and $f(c)>0$ lead to contradictions.

Suppose $f(c)<0$. Then there exists $\delta > 0$ such that

$$f(x)<0 \text { for all } x \in B(c ; \delta) \cap[a, b] .$$

Because $c<b$ (since $f(b)>0$), we can find $s \in(c, b)$ such that $f(s) < 0$ (indeed $s=\min \{c+ \delta / 2,(c+b) / 2\}$ will do). This is a contradiction because $s \in A$ and $s>c$.

Suppose $f(c)>0$. Then there exists $\delta > 0$ such that

$$f(x)>0 \text { for all } x \in B(c ; \delta) \cap[a, b] .$$

Since $a<c$ (because $f(a)<0$), there exists $t \in(a, c)$ such that $f(x)>0$ for all $x \in(t, c)$ (in fact, $t=\max \{c-\delta / 2,(a+c) / 2\}$ will do). On the other hand, since $t<c=\sup A$, there exists $t^{\prime} \in A$ with $t<t^{\prime} \leq c$. But then $t<t^{\prime}$ and $f\left(t^{\prime}\right) \leq 0$. This is a contradiction. We conclude that $f(c)=0$. $\square$

Theorem $\PageIndex{8}$ - Intermediate Value Theorem.

Let $f:[a, b] \rightarrow \mathbb{R}$ be a continuous function. Suppose $f(a)<\gamma<f(b)$. Then there exists a number $c \in(a, b)$ such that $f(c)=\gamma$.

The same conclusion follows if $f(a)>\gamma>f(b)$.

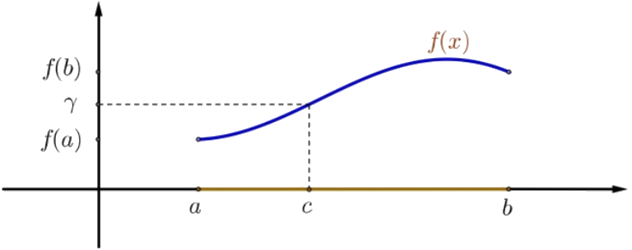
Figure $3.3$: Illustration of the Intermediate Value Theorem.

Proof

Define

$$\varphi(x)=f(x)-\gamma, x \in[a, b] .$$

Then $\varphi$ is continuous on $[a,b]$. Moreover,

$$\varphi(a) \varphi(b)=[f(a)-\gamma][f(b)-\gamma]<0 .$$

By Theorem 3.4.7, there exists $c \in (a,b)$ such that $\varphi(c)=0$. This is equivalent to $f(c)=\gamma$. The proof is now complete. $\square$

Corollary $\PageIndex{9}$

Let $f:[a, b] \rightarrow \mathbb{R}$ be a continuous function. Let

$$m=\min \{f(x): x \in[a, b]\} \text { and } M=\max \{f(x): x \in[a, b]\} .$$

Then for every $\gamma \in[m, M]$, there exists $c \in [a,b]$ such that $f(c)=\gamma$.

Proof

Add proof here and it will automatically be hidden

Example $\PageIndex{1}$

We will use the Intermediate Value Theorem to prove that the equation $e^{x}=-x$ has at least one real solution. We will assume known that the exponential function is continuous on $\mathbb{R}$ and that $e^{x}<1$ for $x<0$.

Solution

First define the function $f: \mathbb{R} \rightarrow \mathbb{R}$ by $f(x)=e^{x}+x$. Notice that the given equation has a solution $x$ if and only if $f(x)=0$. Now, the function $f$ is continuous (as the sum of continuous functions). Moreover, note that $f(-1)=e^{-1}+(-1)<1-1=0$ and $f(0)=1>0$. We can now apply the Intermediate Value Theorem to the function $f$ on the interval $[-1,0]$ with $\gamma=0$ to conclude that there is $c \in [-1,0]$ such that $f(c)=0$. The point $c$ is the desired solution to the original equation.

Example $\PageIndex{2}$

We show now that, given $n \in \mathbb{N}$, every positive real number has a positive $n$-th root.

Solution

Let $n \in \mathbb{N}$ and let $a \in \mathbb{R}$ with $a>0$. First observe that $(1+a)^{n} \geq 1+n a>a$ (see Exercise 1.3.7). Now consider the function $f:[0, \infty) \rightarrow \mathbb{R}$ given by $f(x)=x^{n}$. Since $f(0)=0$ and $f(1+a)>a$, it follows from the Intermediate Value Theorem that there is $x \in(0,1+a)$ such that $f(x)=a$. That is, $x^{n}=a$, as desired. (We show later in Example 4.3.1 that such an $x$ is unique.)

We present below a second proof of Theorem 3.4.8 that does not depend on Theorem 3.4.7, but, instead, relies on the Nested Intervals Theorem (Theorem 2.3.3).

Second Proof of Theorem 3.4.8:

We construct a sequence of nested intervals as follows. Set $a_{1}=a$, $b_{1}=b$, and let $I_{1}=[a, b]$. Let $c_{1}=(a+b) / 2$. If $f\left(c_{1}\right)=\gamma$, we are done. Otherwise, either

$$\begin{array}{l} f\left(c_{1}\right)>\gamma \quad \text { or } \\ f\left(c_{1}\right)<\gamma \end{array} .$$

In the first case, set $a_{2}=a_{1}$ and $b_{1}=c_{1}$. In the second case, set $a_{2}=c_{1}$ and $b_{2}=b_{1}$. Now set $I_{2}=\left[a_{2}, b_{2}\right]$. Note that in either case,

$$f\left(a_{2}\right)<\gamma<f\left(b_{2}\right) .$$

Set $c_{2}=\left(a_{2}+b_{2}\right) / 2$. If $f\left(c_{2}\right)=\gamma$, again we are done. Otherwise, either

$$\begin{array}{l} f\left(c_{2}\right)>\gamma \quad \text { or } \\ f\left(c_{2}\right)<\gamma \end{array} .$$

In the first case, set $a_{3}=a_{2}$ and $b_{3}=c_{2}$. In the second case, set $a_{3}=c_{2}$ and $b_{3}=b_{2}$. Now set $I_{3}=\left[a_{3}, b_{3}\right]$. Note that in either case,

$$f\left(a_{3}\right)<\gamma<f\left(b_{3}\right) .$$

Proceeding in this way, either we find some $c_{n_{0}}$ such that $f\left(c_{n_{0}}\right)=\gamma$ and, hence, the proof is complete, or we construct a sequence of closed bounded intervals $\left\{I_{n}\right\}$ with $I_{n}=\left[a_{n}, b_{n}\right]$ such that for all $n$,

1. $I_{n} \supset I_{n+1}$,
2. $b_{n}-a_{n}=(b-a) / 2^{n-1}$, and
3. $f\left(a_{n}\right)<\gamma<f\left(b_{n}\right)$.

In this case, we proceed as follows. Condition (ii) implies that $\lim _{n \rightarrow \infty}\left(b_{n}-a_{n}\right)=0$. By the Nested Intervals Theorem (Theorem 2.3.3, part(b)), there exists $c \in[a, b]$ such that $\bigcap_{n=1}^{\infty} I_{n}=\{c\}$. Moreover, as we see from the proof of that theorem, $a_{n} \rightarrow c$ and $b_{n} \rightarrow c$ as $n \rightarrow \infty$.

By the continuity of $f$, we get

$$\begin{array}{l} \lim _{n \rightarrow \infty} f\left(a_{n}\right)=f(c) \quad \text { and } \\ \lim _{n \rightarrow \infty} f\left(b_{n}\right)=f(c) \end{array} .$$

Since $f\left(a_{n}\right)<\gamma<f\left(b_{n}\right)$ for all $n$, condition (iii) above and Theorem 2.1.5 give

$$\begin{array}{l} f(c) \leq \gamma \quad \text { and } \\ f(c) \geq \gamma \end{array} .$$

It follows that $f(c)=\gamma$. Note that, since $f(a)<\gamma<f(b)$, then $c \in (a,b)$. The proof is now complete. $\square$

Now we are going to discus the continuity of the inverse function. For a function $f: D \rightarrow E$, where $E$ is a subset of $\mathbb{R}$, we can define the new function $f: D \rightarrow \mathbb{R}$ by the same function notation. The function $f: D \rightarrow E$ is said to be continuous at a point $\bar{x} \in D$ if the corresponding function $f: D \rightarrow \mathbb{R}$ is continuous at $\bar{x}$.

Theorem $\PageIndex{10}$

Let $f:[a, b] \rightarrow \mathbb{R}$ be strictly increasing and continuous on $[a,b]$. Let $c=f(a)$ and $d=f(b)$. Then $f$ is one-to-one, $f([a, b])=[c, d]$, and the inverse function $f^{-1}$ defined on $[c,d]$ by

$$f^{-1}(f(x))=x \text { where } x \in[a, b] ,$$

is a continuous function from $[c,d]$ onto $[a,b]$.

Proof

The first two assertions follow from the monotonicity of $f$ and the Intermediate Value Theorem (see also Corollary 3.4.9). We will prove that $f^{-1}$ is continuous on $[c,d]$. Fix any $\bar{y} \in [c,d]$ and fix any sequence $\left\{y_{k}\right\}$ in $[c,d]$ that converges to $\bar{y}$. Let $\bar{x} \in[a, b]$ and $x_{k} \in[a, b]$ be such that

$$f(\bar{x})=\bar{y} \text { and } f\left(x_{k}\right)=y_{k} \text { for every } k .$$

Then $f^{-1}(\bar{y})=\bar{x}$ and $f^{-1}\left(y_{k}\right)=x_{k}$ for every $k$. Suppose by contradiction that $\left\{x_{k}\right\}$ does not converge to $\bar{x}$. Then there exists $\varepsilon_{0}>0$ and a subsequence $\left\{x_{k_{\ell}}\right\}$ of $\left\{x_{k}\right\}$ such that

$$\left|x_{k_{\ell}}-\bar{x}\right| \geq \varepsilon_{0} \text { for every } \ell .$$

Since the sequence $\left\{x_{k_{\ell}}\right\}$ is bounded, it has a further subsequence that converges to $x_{0} \in[a, b]$. To simplify the notation, we will again call the new subsequence $\left\{x_{k_{\ell}}\right\}$. Taking limits in (3.7), we get

$$\left|x_{0}-\bar{x}\right| \geq \varepsilon_{0}>0 .$$

On the other hand, by the continuity of $f$, $\left\{f\left(x_{k_{\ell}}\right)\right\}$ converges to $f\left(x_{0}\right)$. Since $f\left(x_{k_{\ell}}\right)=y_{k_{\ell}} \rightarrow \bar{y}$ as $\ell \rightarrow \infty$, it follows that $f\left(x_{0}\right)=\bar{y}=f(\bar{x})$. This implies $x_{0}=\bar{x}$, which contradicts (3.8). $\square$

Remark $\PageIndex(11)$

A similar result holds if the domain of $f$ is the open interval $(a,b)$ with some additional considerations. If $f:(a, b) \rightarrow \mathbb{R}$ is increasing and bounded, followin the argument in Theorem 3.2.4 we can show that both $\lim _{x \rightarrow a^{+}} f(x)=c$ and $\lim _{x \rightarrow b^{-}} f(x)=d$ exist in $\mathbb{R}$ (see Exercise 3.2.10). Using the Intermediate Value Theorem we obtain that $f((a, b))=(c, d)$. We can now proceed as in the previous theorem to show that $f$ has a continuous inverse from $(c,d)$ to $(a,b)$.

If $:(a, b) \rightarrow \mathbb{R}$ is increasing, continuous, bounded below, but not bounded above, then $\lim _{x \rightarrow a^{+}} f(x)= c \in \mathbb{R}$, but $\lim _{x \rightarrow b^{-}} f(x)=\infty$ (again see Exercise 3.2.10). In this case we can show using the Intermediate Value Theorem that $f((a, b))=(c, \infty)$ and we can proceed as above to prove that $f$ has a continuous inverse from $(c, \infty)$ to $(a,b)$.

The other possibilities lead to similar results.

A similar theorem can be proved for strictly decreasing functions.

Exercise $\PageIndex{1}$

Let $f: D \rightarrow \mathbb{R}$ be continuous at $c \in D$ and let $\gamma \in \mathbb{R}$. Suppose $f(c)>\gamma$. Prove that there exists $\delta>0$ such that

$$f(x)>\gamma \text { for every } x \in B(c ; \delta) \cap D .$$

Answer

Add texts here. Do not delete this text first.

Exercise $\PageIndex{2}$

Let $f,g$ be continuous functions on $[a,b]$. Suppose $f(a)<g(a)$ and $f(b)>g(b)$. Prove that there exists $x_{0} \in(a, b)$ such that $f\left(x_{0}\right)=g\left(x_{0}\right)$.

Exercise $\PageIndex{3}$

Prove that the equation $\cos x=x$ has at least one solution in $\mathbb{R}$. (Assume known that the function $\cos x$ is continuous.

Exercise $\PageIndex{4}$

Prove that the equation $x^{2}-2=\cos (x+1)$ has at least two real solutions. (Assume known that the function $\cos x$ is continuous.)

Exercise $\PageIndex{5}$

Let $f:[a, b] \rightarrow[a, b]$ be a continuous function.

1. Prove that the equation $f(x)=x$ has a solution on $[a,b]$.
2. Suppose further that

$$|f(x)-f(y)|<|x-y| \text { for all } x, y \in[a, b], x \neq y .$$

Prove that the equation $f(x)=x$ has a unique solution on $[a,b]$

Exercise $\PageIndex{6}$

Let $f$ be a continuous function on $[a,b]$ and $x_{1}, x_{2}, \ldots, x_{n} \in[a, b]$. Prove that there exists $c \in [a,b]$ with

\[f(c)=\frac{f\left(x_{1}\right)+f\left(x_{2}\right)+\cdots f\left(x_{n}\right)}{n}.\

Exercise $\PageIndex{7}$

Suppose $f$ is a continuous function on $\mathbb{R}$ such that $|f(x)| < |x| \text { for all } x \neq 0$.

1. Prove that $f(0)=0$.
2. Given two positive numbers $a$ and $b$ with $a < b$, prove that there exists $\ell \in[0,1)$ such that $$|f(x)| \leq \ell|x| \text { for all } x \in[a, b].$$

Exercise $\PageIndex{8}$

Let $f, g:[0,1] \rightarrow[0,1]$ be continuous functions such that

$$f(g(x))=g(f(x)) \text { for all } x \in[0,1] . \nonumber$$

Suppose further that $f$ is monotone. Prove that there exists $x_{0} \in[0,1]$ such that

$$f\left(x_{0}\right)=g\left(x_{0}\right)=x_{0} . \nonumber$$