4.6: CONVEX FUNCTIONS AND DERIVATIVES
- Page ID
- 49118
We discuss in this section a class of functions that plays an important role in optimization problems.
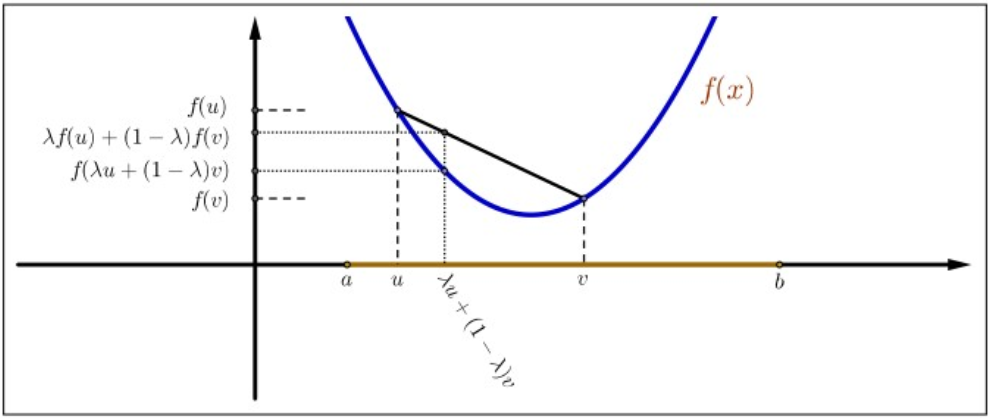
Figure \(4.6\): A Convex Function.
Let \(I\) be an interval of \(\mathbb{R}\) and let \(f: I \rightarrow \mathbb{R}\). We say that \(f\) is convex on \(I\) if \[f(\lambda u+(1-\lambda) v) \leq \lambda f(u)+(1-\lambda) f(v)\] for all \(u, v \in I\) and for all \(\lambda \in (0, 1)\).
The following functions are convex.
- \(f: \mathbb{R} \rightarrow \mathbb{R}\), \(f(x)=x\).
- \(f: \mathbb{R} \rightarrow \mathbb{R}\), \(f(x)=x^{2}\).
- \(f: \mathbb{R} \rightarrow \mathbb{R}\), \(f(x)=|x|\).
Solution
- This is straightforward.
- Here not first that \(2 x y \leq x^{2}+y^{2}\) for all real numbers \(x\), \(y\). Then, if \(0<\lambda<1\) and \(x, y \in \mathbb{R}\), we get \[\begin{aligned}
f(\lambda x+(1-\lambda) y) &=(\lambda x+(1-\lambda) y)^{2} \\
&=\lambda^{2} x^{2}+2 \lambda(1-\lambda) x y+(1-\lambda)^{2} y^{2} \\
& \leq \lambda^{2} x^{2}+\lambda(1-\lambda)\left(x^{2}+y^{2}\right)+(1-\lambda)^{2} y^{2} \\
&=\lambda\left(\lambda x^{2}+(1-\lambda) x^{2}\right)+(1-\lambda)\left(\lambda y^{2}+(1-\lambda) y^{2}\right) \\
&=\lambda x^{2}+(1-\lambda) y^{2} \\
&=\lambda f(x)+(1-\lambda) f(y) \text {.}
\end{aligned}\] - This follows from the triangle inequality and other basic properties of absolute value.
Let \(I\) be an interval of \(\mathbb{R}\). A function \(f: I \rightarrow \mathbb{R}\) is convex if and only if for every \(\lambda_{i} \geq 0, i=1, \ldots, n\), with \(\sum_{i=1}^{n} \lambda_{i}=1\) \((n \geq 2)\) and for every \(x_{i} \in I\), \(\i=1, \dots, n\), \[f\left(\sum_{i=1}^{n} \lambda_{i} x_{i}\right) \leq \sum_{i=1}^{n} \lambda_{i} f\left(x_{i}\right) .\]
- Proof
-
Since the converse holds trivially, we only need to prove that implication by induction. The conclusions holds for \(n = 2\) by the definition of convexity. Let \(k\) be such that the conclusion holds for any \(n\) with \(2 \leq n \leq k\). We will show that it also holds for \(n = k + 1\). Fix \(\lambda_{i} \geq 0, i=1, \ldots, k+1\), with \(\sum_{i=1}^{k+1} \lambda_{i}=1\) and fix every \(x_{i} \in I, i=1, \ldots, k+1\). Then \[\sum_{i=1}^{k} \lambda_{i}=1-\lambda_{k+1} .\] If \(\lambda_{k+1}=1\), then \(\lambda_{i}=0\) for all \(i=1, \ldots, k\), and (4.6.2) holds. Suppose \(0 \leq \lambda_{k+1}<1\). Then, for each \(i=1, \ldots, k\), \(\lambda_{i} /\left(1-\lambda_{k+1}\right) \geq 0\) and \[\sum_{i=1}^{k} \frac{\lambda_{i}}{1-\lambda_{k+1}}=1 .\] It follows that \[\begin{aligned}
f\left(\sum_{i=1}^{k+1} \lambda_{i} x_{i}\right) &=f\left[\left(1-\lambda_{k+1}\right) \frac{\sum_{i=1}^{k} \lambda_{i} x_{i}}{1-\lambda_{k+1}}+\lambda_{k+1} x_{k+1}\right] \\
& \leq\left(1-\lambda_{k+1}\right) f\left(\frac{\sum_{i=1}^{k} \lambda_{i} x_{i}}{1-\lambda_{k+1}}\right)+\lambda_{k+1} f\left(x_{k+1}\right) \\
&=\left(1-\lambda_{k+1}\right) f\left(\sum_{i=1}^{k} \frac{\lambda_{i}}{1-\lambda_{k+1}} x_{i}\right)+\lambda_{k+1} f\left(x_{k+1}\right) \\
& \leq\left(1-\lambda_{k+1}\right) \sum_{i=1}^{k} \frac{\lambda_{i}}{1-\lambda_{k+1}} f\left(x_{i}\right)+\lambda_{k+1} f\left(x_{k+1}\right) \\
&=\sum_{i=1}^{k+1} \lambda_{i} f\left(x_{i}\right) ,
\end{aligned}\] where the first inequality follows from the definition of convexity (or is trivial if \(\lambda_{k+1}=0\)) and the last inequality follows from the inductive assumption. The proof is now complete. \(\square\)
Let \(I\) be an interval and let \(f: I \rightarrow \mathbb{R}\) be a convex function. Then \(f\) has a local minimum at \(\bar{x}\) if and only if \(f\) has an absolute minimum at \(\bar{x}\).
- Proof
-
Clearly if \(f\) has a global minimum at \(\bar{x}\), then it also has a local minimum at \(\bar{x}\).
Conversely, suppose that \(f\) has a local minimum at \(\bar{x}\). Then there exists \(\delta > 0\) such that \[f(u) \geq f(\bar{x}) \text { for all } u \in B(\bar{x} ; \delta) \cap I .\] For any \(x \in I\), we have \(x_{n}=\left(1-\frac{1}{n}\right) \bar{x}+\frac{1}{n} x \rightarrow \bar{x}\). Thus, \(x_{n} \in B(\bar{x} ; \delta) \cap I\) when \(n\) is sufficiently large. Thus, for such \(n\), \[f(\bar{x}) \leq f\left(x_{n}\right) \leq\left(1-\frac{1}{n}\right) f(\bar{x})+\frac{1}{n} f(x) .\] This implies that for a sufficient large \(n\), we have \[\frac{1}{n} f(\bar{x}) \leq \frac{1}{n} f(x)\] and, hence, \(f(\bar{x}) \leq f(x)\). Since \(x\) was arbitrary, this shows \(f\) has an absolute minimum at \(\bar{x}\). \(square\)
Let \(I\) be an open interval and let \(f: I \rightarrow \mathbb{R}\) be a convex function. Suppose \(f\) is differentiable at \(\bar{x}\). Then \[f^{\prime}(\bar{x})(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x \in I .\]
- Proof
-
For any \(x \in I\) and \(t \in (0, 1)\), we have \[\begin{aligned}
\frac{f(\bar{x}+t(x-\bar{x}))-f(\bar{x})}{t} &=\frac{f(t x+(1-t) \bar{x})-f(\bar{x})}{t} \\
& \leq \frac{t f(x)+(1-t) f(\bar{x})-f(\bar{x})}{t} \\
&=f(x)-f(\bar{x}) \text {.}
\end{aligned}\] Since \(f\) is differentiable at \(\bar{x}\), \[f^{\prime}(\bar{x})(x-\bar{x})=\lim _{t \rightarrow 0^{+}} \frac{f(\bar{x}+t(x-\bar{x}))-f(\bar{x})}{t} \leq f(x)-f(\bar{x}) ,\] which completes the proof. \(\square\)
Let \(I\) be open interval and let \(f: I \rightarrow \mathbb{R}\) be a convex function. Suppose \(f\) is differentiable at \(\bar{x}\). Then \(f\) has an absolute minimum at \(\bar{x}\) if and only if \(f^{\prime}(\bar{x})=0\).
- Proof
-
Suppose \(f\) has an absolute minimum at \(\bar{x}\). By Theorem 4.2.1, \(f^{\prime}(\bar{x})=0\). Let us prove the converse. Suppose \(f^{\prime}(\bar{x})=0\). It follows from Theorem 4.6.3 that \[0=f^{\prime}(\bar{x})(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x \in I .\] This implies \[f(x) \geq f(\bar{x}) \text { for all } x \in I .\] Thus, \(f\) has an absolute minimum at \(\bar{x}\). \(\square\)
Let \(I\) be an open interval and suppose \(f: I \rightarrow \mathbb{R}\) is a convex function. Fix \(a, b, x \in I\) with \(a < x < b\). Then \[\frac{f(x)-f(a)}{x-a} \leq \frac{f(b)-f(a)}{b-a} \leq \frac{f(b)-f(x)}{b-x} .\]
- Proof
-
Let \[t=\frac{x-a}{b-a} .\] Then \(t \in (0, 1) \) and \[f(x)=f(a+(x-a))=f\left(a+\frac{x-a}{b-a}(b-a)\right)=f(a+t(b-a))=f(t b+(1-t) a) .\] By convexity of \(f\), we obtain \[f(x) \leq t f(b)+(1-t) f(a) .\] Thus, \[f(x)-f(a) \leq t f(b)+(1-t) f(a)-f(a)=t[f(b)-f(a)]=\frac{x-a}{b-a}(f(b)-f(a)) .\] Equivalently, \[\frac{f(x)-f(a)}{x-a} \leq \frac{f(b)-f(a)}{b-a} .\] Similarly, \[f(x)-f(b) \leq t f(b)+(1-t) f(a)-f(b)=(1-t)[f(a)-f(b)]=\frac{x-b}{b-a}[f(b)-f(a)] .\] It follows that \[\frac{f(b)-f(a)}{b-a} \leq \frac{f(b)-f(x)}{b-x} .\] The proof is now complete. \(\square\)
Let \(I\) be an open interval and let \(f: I \rightarrow \mathbb{R}\) be a differentiable function. Then \(f\) is convex if and only if \(f^{\prime}\) is increasing on \(I\).
- Proof
-
Suppose \(f\) is convex. Fix \(a < b\) with \(a, b \in I\). By Lemma 4.6.5, for any \(x \in (a, b)\), we have \[\frac{f(x)-f(a)}{x-a} \leq \frac{f(b)-f(a)}{b-a} .\] This implies, taking limits, that \[f^{\prime}(a) \leq \frac{f(b)-f(a)}{b-a} .\] Similarly, \[\frac{f(b)-f(a)}{b-a} \leq f^{\prime}(b) .\] Therefore, \(f^{\prime}(a) \leq f^{\prime}(b)\), and \(f^{\prime}\) is an increasing function.
Let us prove the converse. Suppose \(f^{\prime}\) is increasig. Fix \(x_{1}<x_{2}\) and \(t \in (0, 1)\). Then \[x_{1}<x_{t}<x_{2} ,\] where \(x_{t}=t x_{1}+(1-t) x_{2}\). By the Mean Value Theorem (Theorem 4.2.3), there exists \(c_{1}\) and \(c_{2}\) such that \[x_{1}<c_{1}<x_{t}<c_{2}<x_{2}\] with \[\begin{array}{l}
f\left(x_{t}\right)-f\left(x_{1}\right)=f^{\prime}\left(c_{1}\right)\left(x_{t}-x_{1}\right)=f^{\prime}\left(c_{1}\right)(1-t)\left(x_{2}-x_{1}\right) \text {;} \\
f\left(x_{t}\right)-f\left(x_{2}\right)=f^{\prime}\left(c_{2}\right)\left(x_{t}-x_{2}\right)=f^{\prime}\left(c_{2}\right) t\left(x_{1}-x_{2}\right) \text {.}
\end{array}\]l This implies \[\begin{array}{l}
t f\left(x_{t}\right)-t f\left(x_{1}\right)=f^{\prime}\left(c_{1}\right) t(1-t)\left(x_{2}-x_{1}\right) \text {;} \\
(1-t) f\left(x_{t}\right)-(1-t) f\left(x_{2}\right)=f^{\prime}\left(c_{2}\right) t(1-t)\left(x_{1}-x_{2}\right) \text {.}
\end{array}\] Since \(f^{\prime}\left(c_{1}\right) \leq f^{\prime}\left(c_{2}\right)\), we have \[t f\left(x_{t}\right)-t f\left(x_{1}\right)=f^{\prime}\left(c_{1}\right) t(1-t)\left(x_{2}-x_{1}\right) \leq f^{\prime}\left(c_{2}\right) t(1-t)\left(x_{2}-x_{1}\right)=(1-t) f\left(x_{2}\right)-(1-t) f\left(x_{t}\right) .\] Rearranging terms, we get \[f\left(x_{t}\right) \leq t f\left(x_{1}\right)+(1-t) f\left(x_{2}\right) .\] Therefore, \(f\) is convex. The proof is now complete. \(\square\)
Let \(I\) be an open interval and let \(f: I \rightarrow \mathbb{R}\) be a function. Suppose \(f\) is twice differentiable on \(I\). Then \(f\) is convex if and only if \(f^{\prime \prime}(x) \geq 0\) for all \(x \in I\).
- Proof
-
It follows from Proposition 4.3.2 that \(f^{\prime \prime}(x) \geq 0\) for all \(x \in I\) if and only if the derivative function \(f^{\prime}\) is increasing on \(I\). The conclusion then follows directlye from Theorem 4.6.6. \(\square\)
Consider the function \(f: \mathbb{R} \rightarrow \mathbb{R}\) given by \(f(x)=\sqrt{x^{2}+1}\).
Solution
Now, \(f^{\prime}(x)=x / \sqrt{x^{2}+1}\) and \(f^{\prime \prime}(x)=1 /\left(x^{2}+1\right)^{3 / 2}\). Since \(f^{\prime \prime}(x) \geq 0\) for all \(x\), it follows from the corollary that \(f\) is convex.
Let \(I\) be an open interval and let \(f: I \rightarrow \mathbb{R}\) be a convex function. Then it is locally Lipschitz continuous in the sense that for any \(\bar{x} \in I\), there exists \(\ell \geq 0\) and \(\delta > 0\) such that \[|f(u)-f(v)| \leq \ell|u-v| \text { for all } u, v \in B(\bar{x} ; \delta) .\] In particular, \(f\) is continuous.
- Proof
-
Fix any \(\bar{x} \in I\). Choose four numbers \(a, b, c, d\) satisfying \[a<b<\bar{x}<c<d \text { with } a, d \in I .\] Choose \(\delta > 0\) such that \(B(\bar{x} ; \delta) \subset(b, c)\). Let \(u, v \in B(\bar{x} ; \delta)\) with \(v < u\). Then by Lemma 4.6.5, we see that \[\frac{f(b)-f(a)}{b-a} \leq \frac{f(u)-f(a)}{u-a} \leq \frac{f(u)-f(v)}{u-v} \leq \frac{f(d)-f(v)}{d-v} \leq \frac{f(d)-f(c)}{d-c} .\] Using a similar approach for the case \(u < v\), we get \[\frac{f(b)-f(a)}{b-a} \leq \frac{f(u)-f(v)}{u-v} \leq \frac{f(d)-f(c)}{d-c} \text { for all } u, v \in B(\bar{x} ; \delta) .\] Choose \(\ell \geq 0\) sufficiently large so that \[-\ell \leq \frac{f(b)-f(a)}{b-a} \leq \frac{f(u)-f(v)}{u-v} \leq \frac{f(d)-f(c)}{d-c} \leq \ell \text { for all } u, v \in B(\bar{x} ; \delta) .\] Then (4.6.29 holds. The proof is now complete. \(\square\)
Exercise \(\PageIndex{1}\)
- Let \(I\) be an interval and let \(f, g: I \rightarrow \mathbb{R}\) be convex functions. Prove that \(cf\), \(f + g\), and \(\max \{f, g\}\) are convex functions on \(I\), where \(c \geq 0\) is a constant.
- Find two convex functions \(f\) and \(g\) on an interval \(I\) such that \(f \cdot g\) is not convex.
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{2}\)
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function. Given \(a, b \in \mathbb{R}\), prove that the function defined by \[g(x)=f(a x+b), \text { for } x \in \mathbb{R}\] is also a convex function on \(\mathbb{R}\).
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{3}\)
Let \(I\) be an interval and let \(f: I \rightarrow \mathbb{R}\) be a convex function. Suppose that \(\phi\) is a convex, increasing function on an interval \(J\) that contains \(f(I)\). Prove that \(\phi \circ f\) is convex on \(I\).
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{4}\)
Prove that each of the following functions is convex on the given domain:
- \(f(x)=e^{b x}\), \(x \in \mathbb{R}\), where \(b\) is a constant.
- \(f(x)=x^{k}\), \(x \in[0, \infty)\) and \(k \geq 1\) is a constant.
- \(f(x)=-\ln (1-x)\), \(x \in(-\infty, 1)\).
- \(f(x)=-\ln \left(\frac{e^{x}}{1+e^{x}}\right)\), \(x \in \mathbb{R}\).
- \(f(x)=x \sin x\), \(x \in\left(-\frac{\pi}{4}, \frac{\pi}{4}\right)\).
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{5}\)
Prove the following:
- If \(a, b\) are nonnegative real numbers, then \[\frac{a+b}{2} \geq \sqrt{a b} .\]
- If \(a_{1}, a_{2}, \ldots, a_{n}\), where \(n \geq 2\), are nonnegative real numbers, then \[\frac{a_{1}+a_{2}+\cdots+a_{n}}{n} \geq\left(a_{1} \cdot a_{2} \cdots a_{n}\right)^{1 / n} .\]
- Answer
-
Add texts here. Do not delete this text first.


