4.7: NONDIFFERENTIABLE CONVEX FUNCTIONS AND SUBDIFFERENTIALS
- Page ID
- 50413
In this section, we introduce a new concept that is helpful in the study of optimization problems in which the objective function may fail to be differentiable.
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function. A number \(u \in \mathbb{R}\) is called a subderivative of the function \(f\) at \(\bar{x}\) if \[u \cdot(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x \in \mathbb{R} .\] The set of all subderivatives of \(f\) at \(\bar{x}\) is called the subdifferential of \(f\) at \(\bar{x}\) and is denoted by \(\partial f(\bar{x})\).
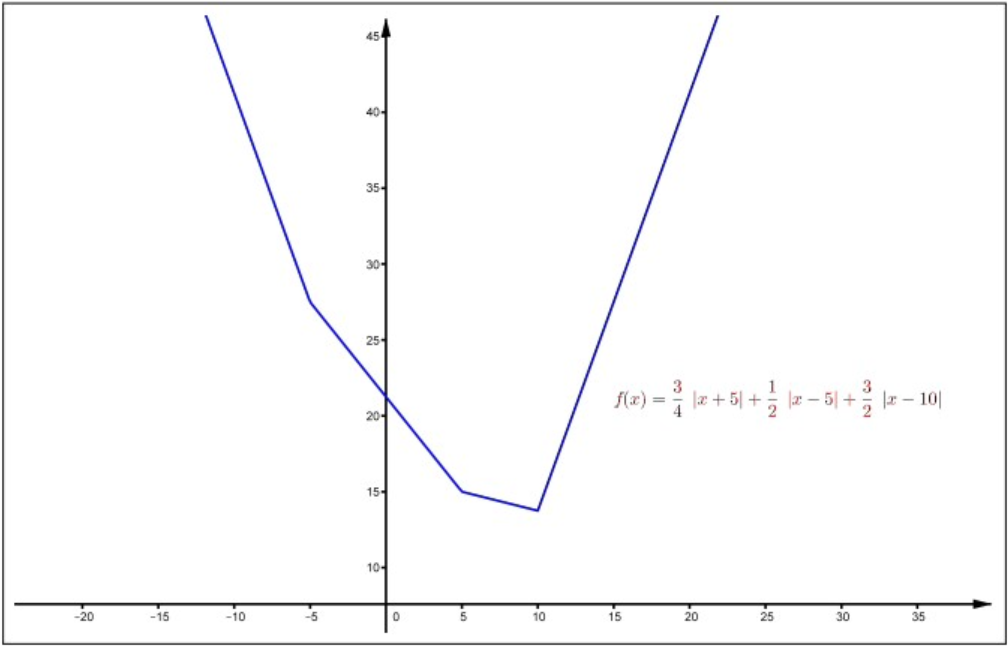
Figure \(4.7\): A nondifferential convex function.
Let \(f(x)=|x|\). Then \[\partial f(0)=[-1,1].\]
Solution
Indeed, for any \(u \in \partial f(0)\), we have \[u \cdot x=u(x-0) \leq f(x)-f(0)=|x| \text { for all } x \in \mathbb{R}.\] In particular, \(u \cdot 1 \leq|1|=1\) and \(u \cdot(-1)=-u \leq|-1|=1\). Thus, \(u \in[-1,1]\). It follows that \[\partial f(0) \subset[-1,1].\] For any \(u \in[-1,1]\), we have \(|u| \leq 1\). Then \[u \cdot x \leq|u \cdot x|=|u||x| \leq|x| \text { for all } x \in \mathbb{R} .\] This implies \(u \in \partial f(0)\). Therefore, \(\partial f(0)=[-1,1]\).
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function, Fix \(a \in \mathbb{R}\). Define the slope function \(\phi_{a}\) by \[\phi_{a}(x)=\frac{f(x)-f(a)}{x-a}\] for \(x \in (-\infty, a) \cup(a, \infty)\). Then, for \(x_{1}, x_{2} \in(-\infty, a) \cup(a, \infty)\) with \(x_{1}<x_{2}\), we have \[\phi_{a}\left(x_{1}\right) \leq \phi_{a}\left(x_{2}\right).\]
- Proof
-
This lemma follows directly from Lemma 4.6.5. \(\square\)
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function and let \(\bar{x} \in \mathbb{R}\). Then \(f\) has left derivative and right derivative at \(\bar{x}\). Moreover, \[\sup _{x<\bar{x}} \phi_{\bar{x}}(x)=f_{-}^{\prime}(\bar{x}) \leq f_{+}^{\prime}(\bar{x})=\inf _{x>\bar{x}} \phi_{\bar{x}}(x) ,\] where \(\phi_{\bar{x}}\) is defined in (4.17).
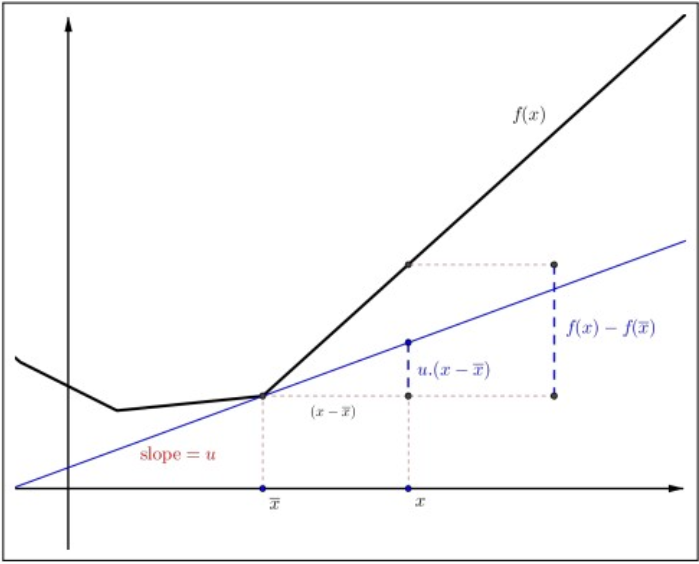
Figure \(4.8\): Definition of subderivative.
- Proof
-
By Lemma 4.7.1, the slope function \(\phi_{x}\) defined by (4.17) is increasing on the interval \((\bar{x}, \infty)\) and bounded below by \(\phi_{\mathcal{K}}(\bar{x}-1)\). By Theorem 3.2.4, the limit \[\lim _{x \rightarrow \bar{x}^{+}} \phi_{i}(x)=\lim _{x \rightarrow \bar{x}^{+}} \frac{f(x)-f(\bar{x})}{x-\bar{x}}\] exists and is finite. Moreover, \[\lim _{x \rightarrow \overline{\mathbf{x}^{+}}} \phi_{x}(x)=\inf _{x>x} \phi_{x}(x) .\] Thus, \(f_{+}^{\prime}(\bar{x})\) exists and \[f_{+}^{\prime}(\bar{x})=\inf _{x>x} \phi_{i}(x) .\] Similarly, \(f_{-}^{\prime}(\bar{x})\) exists and \[f_{-}^{\prime}(\bar{x})=\sup _{x<R} \phi_{x}(x) .\] Applying Lemma 4.7.1 again, we see that \[\phi_{x}(x) \leq \phi_{x}(y) \text { whenever } x<\bar{x}<y .\] This implies \(f_{-}^{\prime}(\bar{x}) \leq f_{+}^{\prime}(\bar{x})\). The proof is complete. \(\square\)
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function and let \(\bar{x} \in \mathbb{R}\). Then \[\partial f(\bar{x})=\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right] .\]
- Proof
-
Suppose \(u \in \partial f(\bar{x})\). By the definition (4.16), we have \[u \cdot(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x>\bar{x} .\] This implies \[u \leq \frac{f(x)-f(\bar{x})}{x-\bar{x}} \text { for all } x>\bar{x} .\] Thus, \[u \leq \lim _{x \rightarrow \bar{x}^{+}} \frac{f(x)-f(\bar{x})}{x-\bar{x}}=f_{+}^{\prime}(\bar{x}) .\] Similarly, we have \[u \cdot(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x<\bar{x} .\] Thus, \[u \geq \frac{f(x)-f(\bar{x})}{x-\bar{x}} \text { for all } x<\bar{x} .\] This implies \(u \geq f_{-}^{\prime}(\bar{x})\). So \[\partial f(\bar{x}) \subset\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right] .\] To prove the opposite inclusion, take \(u \in\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right]\). by Theorem 4.7.2 \[\sup _{x<x} \phi_{\bar{x}}(x)=f_{-}^{\prime}(\bar{x}) \leq u \leq f_{+}^{\prime}(\bar{x})=\inf _{x>\bar{x}} \phi_{\bar{x}}(x) .\] Using the upper estimate by \(f_{+}^{\prime}(\bar{x})\) for \(u\), one has \[u \leq \phi_{\bar{x}}(x)=\frac{f(x)-f(\bar{x})}{x-\bar{x}} \text { for all } x>\bar{x} .\] It follows that \[u \cdot(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x \geq \bar{x} .\] Similarly, one also has \[u \cdot(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x<\bar{x} .\] Thus, (4.16) holds and, hence, \(u \in \partial f(\bar{x})\). Therefore, (4.18) holds. \(\square\)
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function and \(\bar{x} \in \mathbb{R}\). Then \(f\) is differentiable at \(\bar{x}\) if and only if \(\partial f(\bar{x})\) is a singleton. In this case, \[\partial f(\bar{x})=\left\{f^{\prime}(\bar{x})\right\} .\]
- Proof
-
Suppose \(f\) is differentiable at \(\bar{x}\). Then \[f_{-}^{\prime}(\bar{x})=f_{+}^{\prime}(\bar{x})=f^{\prime}(\bar{x}).\] By Theorem 4.7.3, \[\partial f(\bar{x})=\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right]=\left\{f^{\prime}(\bar{x})\right\} .\] Thus, \(\partial f(\bar{x})\) is a singleton.
Conversely, if \(\partial f(\bar{x})\) is a singleton, we must have \(f_{-}^{\prime}(\bar{x})=f_{+}^{\prime}(\bar{x})\). Thus, \(f\) is differentaible at \(\bar{x}\). \(\square\)
Let \(f(x)=a|x-b|+c\), where \(a > 0\).
Solution
Then \(f\) is a convex function and \[f_{-}^{\prime}(b)=-a, f_{+}^{\prime}(b)=a .\] Thus, \[\partial f(b)=[-a, a] .\] Since \(f\) is differentiable on \((-\infty, b)\) and \((b, \infty)\), we have \[\partial f(x)=\left\{\begin{array}{ll}
\{-a\}, & \text { if } x<b \text {;}\\
{[-a, a],} & \text { if } x=b \text {;}\\
\{a\}, & \text { if } x>b \text {.}
\end{array}\right.\]
Let \(A\) and \(B\) be two nonempty subsets of \(\mathbb{R}\) and \(\alpha \in \mathbb{R}\). Define \[A+B=\{a+b: a \in A, b \in B\} \text { and } \alpha A=\{\alpha a: a \in A\} .\]
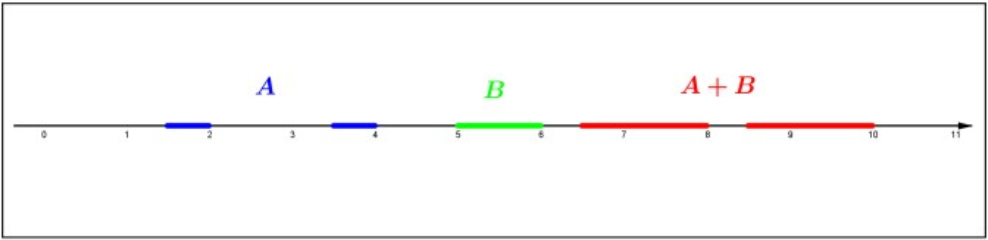
Figure \(4.9\): Set addition.
Let \(f, g: \mathbb{R} \rightarrow \mathbb{R}\) be convex functions and let \(\alpha > 0\). Then \(f + g\) and \(\alpha f\) are convex functions and \[\begin{array}{l}
\partial(f+g)(\bar{x})=\partial f(\bar{x})+\partial g(\bar{x}) \\
\partial(\alpha f)(\bar{x})=\alpha \partial f(\bar{x}) \text {.}
\end{array}\]
- Proof
-
It is not hard to see that \(f + g\) is a convex function and \[\begin{array}{l}
(f+g)_{+}^{\prime}(\bar{x})=f_{+}^{\prime}(\bar{x})+g_{+}^{\prime}(\bar{x}) \\
(f+g)_{-}^{\prime}(\bar{x})=f_{-}^{\prime}(\bar{x})+g_{-}^{\prime}(\bar{x}) \text {.}
\end{array}\] By Theorem 4.7.3, \[\begin{aligned}
\partial(f+g)(\bar{x}) &=\left[(f+g)_{-}^{\prime}(\bar{x}),(f+g)_{+}^{\prime}(\bar{x})\right] \\
&=\left[f_{-}^{\prime}(\bar{x})+g_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})+g_{+}^{\prime}(\bar{x})\right] \\
&=\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right]+\left[g_{-}^{\prime}(\bar{x}), g_{+}^{\prime}(\bar{x})\right] \\
&=\partial f(\bar{x})+\partial g(\bar{x}) \text {.}
\end{aligned}\] The proof for the second formula is similar. \(\square\)
Let \(a_{1}<a_{2}<\cdots<a_{n}\) and let \(\mu_{i}>0\) for \(i=1, \ldots, n\). Define \[f(x)=\sum_{i=1}^{n} \mu_{i}\left|x-a_{i}\right| .\]
Solution
Then \(f\) is a convex function. By Theorem 4.7.5, we get \[\partial f(\bar{x})=\left\{\begin{array}{ll}
\sum_{a_{i}<\bar{x}} \mu_{i}-\sum_{a_{i}>\bar{x}} \mu_{i}, & \text { if } \bar{x} \notin\left\{a_{1}, \ldots, a_{n}\right\} \\
\sum_{a_{i}<\bar{x}} \mu_{i}-\sum_{a_{i}>\bar{x}} \mu_{i}+\left[-\mu_{i_{0}}, \mu_{i_{0}}\right], & \text { if } \bar{x}=a_{i_{0}} \text {.}
\end{array}\right.\]
Let \(f_{i}: \mathbb{R} \rightarrow \mathbb{R}\), \(i=1, \ldots, n\), be convex functions. Define \[f(x)=\max \left\{f_{i}(x): i=1, \ldots, n\right\} \text { and } I(u)=\left\{i=1, \ldots, n: f_{i}(u)=f(u)\right\} .\] Then \(f\) is a convex function. Moreover, \[\partial f(\bar{x})=[m, M],\] where \[m=\min _{i \in I(\bar{x})} f_{i-}^{\prime}(\bar{x}) \text { and } M=\max _{i \in I(\bar{x})} f_{i+}^{\prime}(\bar{x}) .\]
- Proof
-
Fix \(u, v \in \mathbb{R}\) and \(\lambda \in (0, 1)\). For any \(i=1, \ldots, n\), we have \[f_{i}(\lambda u+(1-\lambda) v) \leq \lambda f_{i}(u)+(1-\lambda) f_{i}(v) \leq \lambda f(u)+(1-\lambda) f(v) .\] This implies \[f(\lambda u+(1-\lambda) v)=\max _{1 \leq i \leq n} f_{i}(\lambda u+(1-\lambda) v) \leq \lambda f(u)+(1-\lambda) f(v) .\] Thus, \(f\) is a convex function. Similarly we verify that \(f_{+}^{\prime}(\bar{x})=M\) and \(f_{-}^{\prime}(\bar{x})=m\). By Theorem 4.7.3, \[\partial f(\bar{x})=[m, M] .\] The proof is now complete. \(\square\)
the product of two convex functions is not a convex function in general. For instance, \(f(x) = x\) and \(g(x) = x^{2}\) are convex functions, but \(h(x)=x^{3}\) is not a convex function.
The following result may be considered as a version of the first derivative test for extrema in the case of non differentiable functions.
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function. Then \(f\) has an absolute minimum at \(\bar{x}\) if and only if \[0 \in \partial f(\bar{x})=\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right] .\]
- Proof
-
Suppose \(f\) has an absolute minimum at \(\bar{x}\). Then \[f(\bar{x}) \leq f(x) \text { for all } x \in \mathbb{R} .\] This implies \[0 \cdot(x-\bar{x})=0 \leq f(x)-f(\bar{x}) \text { for all } x \in \mathbb{R} .\] It follows from (4.16) that \(0 \in \partial f(\bar{x})\).
Conversely, if \(0 \in \partial f(\bar{x})\), again, by (4.16), \[0 \cdot(x-\bar{x})=0 \leq f(x)-f(\bar{x}) \text { for all } x \in \mathbb{R} .\] Thus, \(f\) has an absolute minimum at \(\bar{x}\). \(\square\)
Let \(k\) be a positive integer and \(a_{1}<a_{2}<\cdots<a_{2 k-1}\). Define \[f(x)=\sum_{i=1}^{2 k-1}\left|x-a_{i}\right| ,\] for \(x \in \mathbb{R}\).
Solution
It follows from the subdifferential formula in Example 4.7.3 that \(0 \in \partial f(\bar{x})\) if and only if \(\bar{x}=a_{k}\). Thus, \(f\) has a unique absolute minimum at \(a_{k}\).
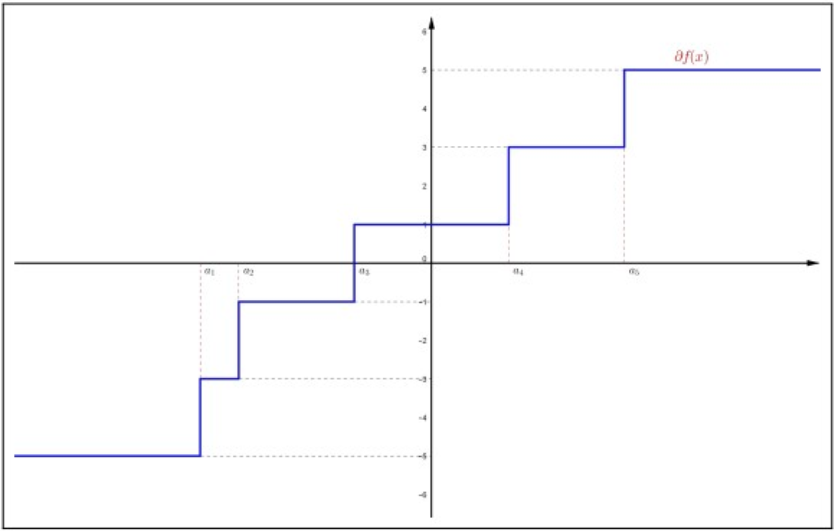
Figure \(4.10\): Subdifferential of \(f(x)=\sum_{i=1}^{2 k-1}\left|x-a_{i}\right|\).
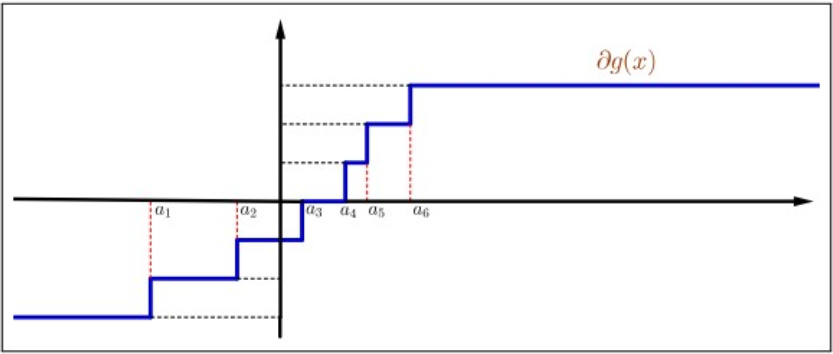
Figure \(4.11\): Subdifferential of \(g(x)=\sum_{i=1}^{2 k}\left|x-a_{i}\right|\).
Similarly, if \(a_{1}<a_{2}<\cdots<a_{2 k}\) and \[g(x)=\sum_{i=1}^{2 k}\left|x-a_{i}\right| .\] Then \(0 \in \partial g(\bar{x})\) if and only if \(\bar{x} \in\left[a_{k}, a_{k+1}\right]\). Thus, \(g\) has an absolute minimum at any point of \(\left[a_{k}, a_{k+1}\right]\).
The following theorem is a version of the Mean Value Theorem (Theorem 4.2.3) for nondifferentiable functions.
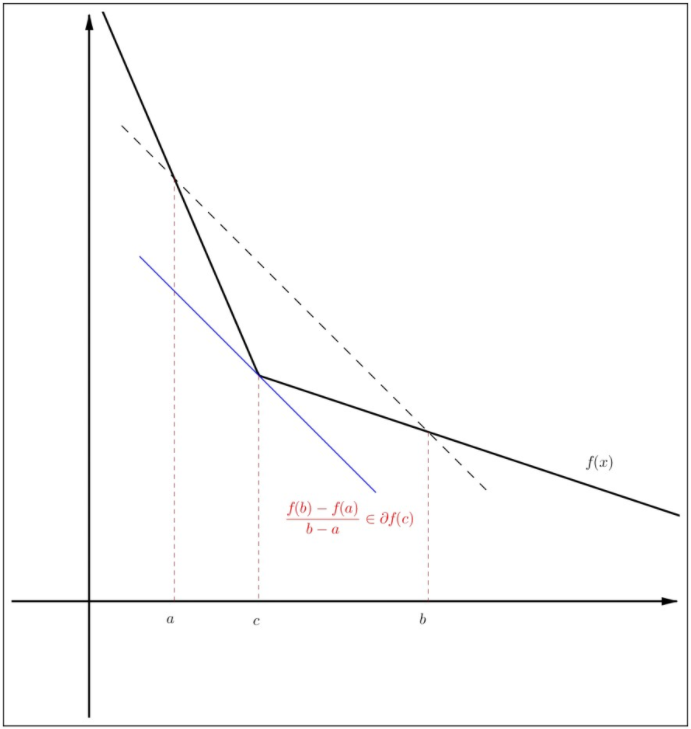
Figure \(4.12\): Subdifferential mean value theorem.
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function and let \(a < b\). Then there exists \(c \in (a, b)\) such that \[\frac{f(b)-f(a)}{b-a} \in \partial f(c) .\]
- Proof
-
Define \[g(x)=f(x)-\left[\frac{f(b)-f(a)}{b-a}(x-a)+f(a)\right] .\] Then \(g\) is a convex function and \(g(a)=g(b)\). Thus, \(g\) has a local minimum at some \(c \in (a, b)\) and, hence, \(g\) also has an absolute minimum at \(c\). Observe that the function \[h(x)=-\left[\frac{f(b)-f(a)}{b-a}(x-a)+f(a)\right]\] is differentiable at \(c\) and, hence, \[\partial h(c)=\left\{h^{\prime}(c)\right\}=\left\{-\frac{f(b)-f(a)}{b-a}\right\} .\] By Theorem 4.7.8 and the subdifferential sum rule, \[0 \in \partial g(c)=\partial f(c)-\left\{\frac{f(b)-f(a)}{b-a}\right\} .\] This implies (4.19). The proof is now complete. \(\square\)
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function. Then \(f\) is Lipschitz continuous if and only if there exists \(\ell \geq 0\) such that \[\partial f(x) \subset[-\ell, \ell] \text { for all } x \in \mathbb{R} .\]
- Proof
-
Suppose \(f\) is Lipschitz continuous on \(\mathbb{R}\). Then there exists \(\ell \geq 0\) such that \[|f(u)-f(v)| \leq \ell|u-v| \text { for all } u, v \in \mathbb{R} .\] Then for any \(x \in \mathbb{R}\), \[f_{+}^{\prime}(x)=\lim _{h \rightarrow 0^{+}} \frac{f(x+h)-f(x)}{h} \leq \lim _{h \rightarrow 0^{+}} \frac{\ell|h|}{h}=\ell .\] Similarly, \(f_{-}^{\prime}(x) \geq-\ell\). Thus, \[\partial f(x)=\left[f_{-}^{\prime}(x), f_{+}^{\prime}(x)\right] \subset[-\ell, \ell] .\] Conversely, fix any \(u, v \in \mathbb{R}\) with \(u \neq v\). Applying Theorem 4.7.9, we get \[\frac{f(v)-f(u)}{v-u} \in \partial f(c) \subset[-\ell, \ell] ,\] for some \(c\) in between \(u\) and \(v\). This implies \[|f(u)-f(v)| \leq \ell|u-v| .\] This inequality obviously holds for \(u = v\). Therefore, \(f\) is Lipschitz continuous. \(\square\)
Exercise \(\PageIndex{1}\)
Find subdifferentials of the following functions:
- \(f(x)=a|x|\), \(a > 0\).
- \(f(x)=|x-1|+|x+1|\).
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{2}\)
Find the subdifferential of the function \[f(x)=\max \{-2 x+1, x, 2 x-1\} .\]
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{3}\)
Let \(f(x)=\sum_{k=1}^{n}|x-k|\). Find all absolute minimizers of the function.
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{4}\)
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function. Fix \(a, b \in \mathbb{R}\) and define the function \(g\) by \[g(x)=f(a x+b), \text { for } x \in \mathbb{R}\] Prove that \(\partial g(\bar{x})=a \partial f(a \bar{x}+b)\).
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{5}\)
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a convex function. Suppose that \(\partial f(x) \subset[0, \infty)\) for all \(x \in \mathbb{R}\). Prove that \(f\) is monotone increasing on \(\mathbb{R}\).
- Answer
-
Add texts here. Do not delete this text first.


