5.11: Integral Definitions of Some Functions
This page is a draft and is under active development.
( \newcommand{\kernel}{\mathrm{null}\,}\)
By Theorem 2 in §10, ∫f exists on I whenever the function f:E1→E is regulated on I, and E is complete. Hence whenever such an f is given, we can define a new function F by setting
F=∫xaf
on I for some a∈I. This is a convenient method of obtaining new continuous functions, differentiable on I−Q (Q countable). We shall now apply it to obtain new definitions of some functions previously defined in a rather strenuous step-by-step manner.
I. Logarithmic and Exponential Functions. From our former definitions, we proved that
lnx=∫x11tdt,x>0.
Now we want to treat this as a definition of logarithms. We start by setting
f(t)=1t,t∈E1,t≠0,
and f(0)=0.
Then f is continuous on I=(0,+∞) and J=(−∞,0), so it has an exact primitive on I and J separately (not on E1). Thus we can now define the log function on I by
∫x11tdt=logx (also written lnx) for x>0.
By the very definition of an exact primitive, the log function is continuous and differentiable on I=(0,+∞); its derivative on I is f. Thus we again have the symbolic formula
(logx)′=1x,x>0.
If x<0, we can consider log(−x). Then the chain rule (Theorem 3 of §1) yields
(log(−x))′=1x. (Verify!)
Hence
(log|x|)′=1x for x≠0.
Other properties of logarithms easily follow from (1). We summarize them now.
(i) log1=∫111tdt=0.
(ii) logx<logy whenever 0<x<y.
(iii) limx→+∞logx=+∞ and limx→0+logx=−∞.
(iv) The range of log is all of E1.
(v) For any positive x,y∈E1,
log(xy)=logx+logy and log(xy)=logx−logy.
(vi) logar=r⋅loga,a>0,r∈N.
(vii) loge=1, where e=limn→∞(1+1n)n.
- Proof
-
(ii) By (2), (logx)′>0 on I=(0,+∞), so logx is increasing on I.
(iii) By Theorem 5 in §10,
limx→+∞logx=∫∞11tdt=+∞
since
∞∑n=11n=+∞(Chapter 4, §13, Example (b)).
Hence, substituting y=1/x, we obtain
limy→0+logy=limx→+∞log1x.
However, by Theorem 2 in §5 (substituting s=1/t),
log1x=∫1/x11tdt=−∫x11sds=−logx.
Thus
limy→0+logy=limx→+∞log1x=−limx→+∞logx=−∞
as claimed. (We also proved that log1x=−logx.)
(iv) Assertion (iv) now follows by the Darboux property (as in Chapter 4, §9, Example (b)).
(v) With x,y fixed, we substitute t=xs in
∫xy11tdt=logxy
and obtain
logxy=∫xy11tdt=∫y1/x1sds=∫11/x1sds+∫y11sds=−log1x+logy=logx+logy.
Replacing y by 1/y here, we have
logxy=logx+log1y=logx−logy.
Thus (v) is proved, and (vi) follows by induction over r.
(vii) By continuity,
loge=limx→elogx=limn→∞log(1+1n)n=limn→∞log(1+1/n)1/n,
where the last equality follows by (vi). Now, L'Hôpital's rule yields
limx→0log(1+x)x=limx→011+x=1.
Letting x run over 1n→0, we get (vii). ◻
Note 1. Actually, (vi) holds for any r∈E1, with ar as in Chapter 2, §§11-12. One uses the techniques from that section to prove it first for rational r, and then it follows for all real r by continuity. However, we prefer not to use this now.
Next, we define the exponential function ("exp") to be the inverse of the log function. This inverse function exists; it is continuous (even differentiable) and strictly increasing on its domain (by Theorem 3 of Chapter 4, §9 and Theorem 3 of Chapter 5, §2) since the log function has these properties. From (logx)′=1/x we get, as in 2,
(expx)′=expx(cf. §2, Example (B)).
The domain of the exponential is the range of its inverse, i.e., E1 (cf. Theorem 1(iv)). Thus expx is defined for all x∈E1. The range of exp is the domain of log, i.e., (0,+∞). Hence exp x>0 for all x∈E1. Also, by definition,
exp(logx)=x for x>0exp0=1 (cf. Theorem 1(i)), and expr=er for r∈N.
Indeed, by Theorem 1(vi) and (vii), log er=r⋅loge=r. Hence (6) follows. If the definitions and rules of Chapter 2, §§11-12 are used, this proof even works for any r by Note 1. Thus our new definition of exp agrees with the old one.
Our next step is to give a new definition of ar, for any a,r∈E1(a>0). We set
ar=exp(r⋅loga) or logar=r⋅loga(r∈E1).
In case r∈N, (8) becomes Theorem 1(vi). Thus for natural r, our new definition of ar is consistent with the previous one. We also obtain, for a,b>0,
(ab)r=arbr;ars=(ar)s;ar+s=aras;(r,s∈E1).
The proof is by taking logarithms. For example,
log(ab)r=rlogab=r(loga+logb)=r⋅loga+r⋅logb=logar+logbr=log(arbr).
Thus (ab)r=arbr. Similar arguments can be given for the rest of (9) and other laws stated in Chapter 2, §§11-12.
We can now define the exponential to the base a(a>0) and its inverse, log a, as before (see the example in Chapter 4, §5 and Example (b) in Chapter 4, §9). The differentiability of the former is now immediate from (7), and the rest follows as before.
II. Trigonometric Functions. These shall now be defined in a precise analytic manner (not based on geometry).
We start with an integral definition of what is usually called the principal value of the arcsine function,
arcsinx=∫x01√1−t2dt.
We shall denote it by F(x) and set
f(x)=1√1−x2 on I=(−1,1).
(F=f=0 on E1−I.) Thus by definition, F=∫f on I.
Note that ∫f exists and is exact on I since f is continuous on I. Thus
F′(x)=f(x)=1√1−x2>0for x∈I,
and so F is strictly increasing on I. Also, F(0)=∫00f=0.
We also define the number π by setting
π2=2arcsin√12=2F(c)=2∫c0f,c=√12.
Then we obtain the following theorem.
F has the limits
F(1−)=π2 and F(−1+)=−π2.
Thus F becomes relatively continuous on ¯I=[−1,1] if one sets
F(1)=π2 and F(−1)=−π2,
i.e.,
arcsin1=π2 and arcsin(−1)=−π2.
- Proof
-
We have
F(x)=∫x0f=∫c0f+∫xcf,c=√12.
By substituting s=√1−t2 in the last integral and setting, for brevity, y= √1−x2, we obtain
∫xcf=∫xc1√1−t2dt=∫cy1√1−s2ds=F(c)−F(y).(Verify!)
Now as x→1−, we have y=√1−x2→0, and hence F(y)→F(0)=0 (for F is continuous at 0). Thus
F(1−)=limx→1−F(x)=limy→0(∫c0f+∫cyf)=∫c0f+F(c)=2∫c0f=π2.
Similarly, one gets F(−1+)=−π/2.◻
The function F as redefined in Theorem 2 will be denoted by F0. It is a primitive of f on the closed interval ¯I (exact on I). Thus F0(x)=∫x0f, −1≤x≤1, and we may now write
π2=∫10f and π=∫0−1f+∫10f=∫1−1f.
Note 2. In classical analysis, the last integrals are regarded as so-called improper integrals, i.e., limits of integrals rather than integrals proper. In our theory, this is unnecessary since F0 is a genuine primitive of f on ¯I.
For each integer n (negatives included), we now define Fn:E1→E1 by
Fn(x)=nπ+(−1)nF0(x) for x∈¯I=[−1,1]Fn=0 on −¯I.
Fn is called the n th branch of the arcsine. Figure 26 shows the graphs of F0 and F1 ( that of F1 is dotted). We now obtain the following theorem.
(i) Each Fn is differentiable on I=(−1,1) and relatively continuous on ¯I=[−1,1].
(ii) Fn is increasing on ¯I if n is even, and decreasing if n is odd.
(iii) F′n(x)=(−1)n√1−x2 on I.
(iv) Fn(−1)=Fn−1(−1)=nπ−(−1)nπ2;Fn(1)=Fn−1(1)=nπ+(−1)nπ2.
- Proof
-
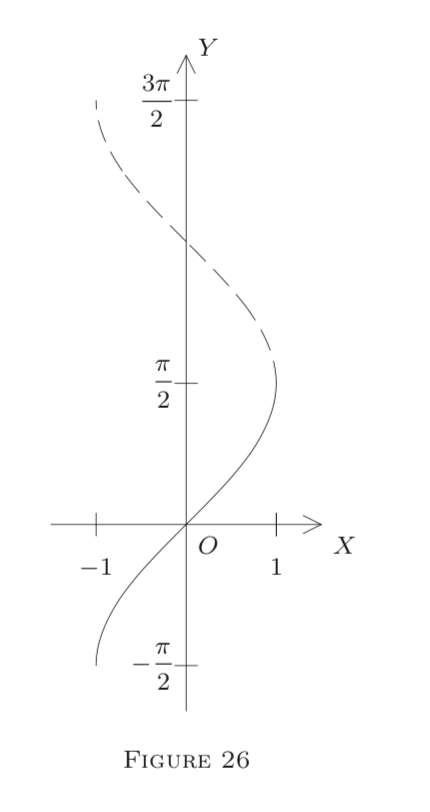
The proof is obvious from (12) and the properties of F0. Assertion (iv) ensures that the graphs of the Fn add up to one curve. By (ii), each Fn is one to one (strictly monotone) on ¯I. Thus it has a strictly monotone inverse on the interval ¯Jn=Fn [[−1,1]], i.e., on the Fn -image of ¯I. For simplicity, we consider only
¯J0=[−π2,π2] and J1=[π2,3π2],
as shown on the Y -axis in Figure 26. On these, we define for x∈¯J0
sinx=F−10(x)
and
cosx=√1−sin2x,
and for x∈¯J1
sinx=F−11(x)
and
cosx=−√1−sin2x.
On the rest of E1, we define sinx and cosx periodically by setting
sin(x+2nπ)=sinx and cos(x+2nπ)=cosx,n=0,±1,±2,….
Note that by Theorem 3(iv),
F−10(π2)=F−11(π2)=1.
Thus (13) and (14) both yield sinπ/2=1 for the common endpoint π/2 of ¯J0 and ¯J1, so the two formulas are consistent. We also have
sin(−π2)=sin(3π2)=−1,
in agreement with (15). Thus the sine and cosine functions (briefly, s and c) are well defined on E1.
The sine and cosine functions (s and c) are differentiable, hence continuous, on all of E1, with derivatives s′=c and c′=−s; that is,
(sinx)′=cosx and (cosx)′=−sinx.
- Proof
-
It suffices to consider the intervals ¯J0 and ¯J1, for by (15), all properties of s and c repeat themselves, with period 2π, on the rest of E1.
By (13),
s=F−10 on ¯J0=[−π2,π2],
where F0 is differentiable on I=(−1,1). Thus Theorem 3 of §2 shows that s is differentiable on J0=(−π/2,π/2) and that
s′(q)=1F′0(p) whenever p∈I and q=F0(p);
i.e., q∈J and p=s(q). However, by Theorem 3(iii),
F′0(p)=1√1−p2.
Hence,
s′(q)=√1−sin2q=cosq=c(q),q∈J.
This proves the theorem for interior points of ¯J0 as far as s is concerned.
As
c=√1−s2=(1−s2)12 on J0 (by (13)),
we can use the chain rule (Theorem 3 in §1) to obtain
c′=12(1−s2)−12(−2s)s′=−s
on noting that s′=c=(1−s2)12 on J0. Similarly, using (14), one proves that s′=c and c′=−s on J1 (interior of ¯J1).
Next, let q be an endpoint, say, q=π/2. We take the left derivative
s′−(q)=limx→q−s(x)−s(q)x−q,x∈J0.
By L'Hôpital's rule, we get
s′−(q)=limx→q−s′(x)1=limx→q−c(x)
since s′=c on J0. However, s=F−10 is left continuous at q (why?); hence so is c=√1−s2. (Why?) Therefore,
s′−(q)=limx→q−c(x)=c(q),as required.
Similarly, one shows that s′+(q)=c(q). Hence s′(q)=c(q) and c′(q)=−s(q) as before. ◻
The other trigonometric functions reduce to s and c by their defining formulas
tanx=sinxcosx,cotx=cosxsinx,secx=1cosx, and cscx=1sinx,
so we shall not dwell on them in detail. The various trigonometric laws easily follow from our present definitions; for hints, see the problems below.


