5.3: Complex Eigenvalues
- Page ID
- 407
In the last section, we found that if
\[\textbf{x}'=A\textbf{x} \]
is a homogeneous linear system of differential equations, and \(r\) is an eigenvalue with eigenvector z, then
\[ \textbf{x}=\textbf{z}e^{rt} \]
is a solution. (Note that x and z are vectors.) In this discussion we will consider the case where \(r\) is a complex number
\[r = l + mi.\]
First we know that if \(r = l + mi\) is a complex eigenvalue with eigenvector z, then
\[r = l - mi\]
the complex conjugate of \(r\) is also an eigenvalue with eigenvector z. We can write the solution as
\[\textbf{x}=k_1\textbf{z}e^{(l+mi)t}+ k_2\textbf{z}e^{(l-mi)t}. \]
We can use Euler's formula to get
\[\textbf{x}=k_1 \textbf{z} e^{lt}(\cos(mt)+i\sin(mt))+ k_2 \textbf{z}e^{lt}(\cos(mt)-i\sin(mt)).\]
Writing
\[\textbf{z}=\textbf{a}+\textbf{a}i \;\;\; \text{and} \;\;\; \textbf{z}=\textbf{a}-\textbf{a}i\]
we get
\[\textbf{x}=k_1 (\textbf{a}+\textbf{b}i)e^{lt}(\cos(mt)+i\sin(mt))+ k_2 (\textbf{a}-\textbf{b}i)e^{lt}(\cos(mt)-i\sin(mt)). \]
Now multiplying and separating into real and imaginary parts, we get
\[\textbf{x}=e^{lt}[k_1(\textbf{a} \cos(mt)- \textbf{b} \sin(mt) + i(\textbf{a} \sin(mt)+ \textbf{b} \cos(mt)) \\ + k_2(\textbf{a} \cos(mt)- \textbf{b} \sin(mt) - i(\textbf{a} \sin(mt)+ \textbf{b} \cos(mt))]. \]
Now let
\[k_1+k_2=2c_1 \;\;\; \text{and} \;\;\; (k_1-k_2)i=2c_2 . \]
Then we get
\[\textbf{x} =e^{lt}[c_1 (\textbf{a} \cos(mt) - \textbf{b} \sin(mt) + c_2 (\textbf{a} \sin(mt) + \textbf{b} \cos(mt))) ] . \]
Solve the system of differential equations
\[x'=-2x+6y \]
\[y'=-3x+4y. \]
Solution
We have
\[A=\begin{pmatrix} -2 &6 \\ -3 &4 \end{pmatrix} \]
To find the eigenvalues, we find the determinant of
\[A-rl = \begin{pmatrix} -2-r & 6 \\ -3 & 4-r \end{pmatrix} . \]
We get
\[(-2-r)(4-r)+18 = r^2-2r+10=0. \]
The quadratic formula gives the roots
\[r=1+3i \;\;\; \text{and} \;\;\; r=1-3i . \]
Now we find and eigenvector corresponding to the eigenvalue \(1 + 3i\). Plugging into \(A - rI\), we get
\[A-(1+3i)l = \begin{pmatrix} -3-3i & 6 \\ -3 &3-3i \end{pmatrix}. \]
The top row gives
\[(-3 - 3i)x + 6y = 0\]
or
\[(1 + i)x - 2y = 0.\]
An eigenvector is
\[z=\begin{pmatrix} 2 \\ 1+i \end{pmatrix}= \begin{pmatrix} 2 \\ 1 \end{pmatrix} + i\begin{pmatrix} 0 \\ 1 \end{pmatrix}. \]
Hence the general solution is
\[x=e^t \left[ c_1\left( \begin{pmatrix}2\\1\end{pmatrix}\cos(3t)-\begin{pmatrix}0\\1\end{pmatrix}\sin(3t) \right) + c_2 \left(\begin{pmatrix}2\\1\end{pmatrix}\sin(3t) + \begin{pmatrix}0\\1\end{pmatrix} \cos(3t) \right) \right] .\]
This can be written as
\[ x=e^t [2c_1 \cos(3t) + 2c_2\sin(2t) ] \]
\[y=e^t[c_1 (\cos(3t)+\sin(3t)) + c_2 (\sin(3t)+ \cos(3t) )] . \]
Below is the phase portrait
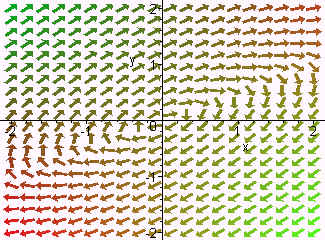
Clearly the solutions spiral out from the origin, which is called a spiral node. The spiral occurs because of the complex eigenvalues and it goes outward because the real part of the eigenvalue is positive. If the real part of the eigenvalue had been negative, then the spiral would have been inward.
Contributors and Attributions
- Larry Green (Lake Tahoe Community College)


