Taylor Expansion

The special type of series known as Taylor series, allow us to express any mathematical function, real or complex, in terms of its n derivatives. The Taylor series can also be called a power series as each term is a power of \(x\), multiplied by a different constant

\[ f(x) = a_0x^0 +a_1x^1 +a_2x^2 +a_3x^3 +... a_nx^n \]

\(a_0, \; a_1,\dots,a_n\) are determined by the functions derivatives. For example the constant \(a_3\) is based on the function's third derivative, \(a_6\) on the sixth derivative or \(f^{(6)}x\) and so on.

It is obvious that a function with a finite number of derivatives would have a finite number of terms, as \(f(x)=x^4,\; f'(x)=4x^3, \; f''(x)=12x^2, \; f'''(x)=24x, \; f^{(4)}(x)=24\). On the other hand, infinitely differentiable functions such as exponential and trigonometric functions would be expressed as an infinite series, whose accuracy in expressing the function would be determined by the number of terms of the series used.

The proof of Taylor's Theorem involves a combination of the Fundamental Theorem of Calculus and the Mean Value Theorem, where we are integrating a function, \(f^{(n)}(x)\) to get \(f(x)\). These two theorems say:

\[\begin{align} & \text{F.T.C:}\; &\int_{a}^{x}f^{(n)}(x) \cdot \Delta x&=f^{(n-1)}(x)-f^{(n-1)}(a) \\& \text{M.V.T:}\; &\int_{a}^{x}f^{(n)}(x) \cdot \Delta x&=f^{(n)}(c)\cdot(x-a) .\end{align}\]

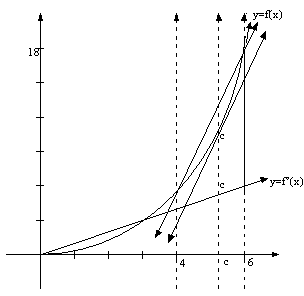
A quick review of the mean value theorem tells us that:

\[\int_{a}^{x} f'(x) \cdot \Delta x =f'(c)\cdot (x-a).\]

.

We therefore know:

\[ f^{(n)}(c)\cdot(x-a)=\int_{a}^{x}f^{(n)}(x)\cdot \Delta (x) = f^{(n-1)}(x)-f^{(n-1)}(a)\]

or

\[f^{(n)}(c)\cdot(x-a)=f^{(n-1)}(x)-f^{(n-1)}(a). \]

We can now integrate the function \(f=f^{(n)}(x)\) once. Integrating the left side gives us:

\[\int_{a}^{x}f^{(n)}(c)\cdot(x-a)\cdot \Delta x =f^{(n)}(c)\int_{a}^{x} (x-a)=f^{(n)}(c)\dfrac{(x-a)^2}{2} .\]

\(f^{(n)}(x)\) is just a constant, and is equal to the \(n\)th derivative evaluated at some point \(c\), between \(a\) and \(x\).

And integrating the right side:

\[\begin{align} \int_{a}^{x}f^{(n-1)}(x)\cdot \Delta x-\int_{a}^{x}f^{(n-1)}(a) \cdot \Delta x &= \left[ f^{(n-2)}(x)-f^{(n-2)}(a) \right]-f^{(n-1)}(a)\int_{a}^{x} \Delta x \\ &\text{(Remembering $f^{(n-1)}(a)$ is a constant)} \\ &=\left[f^{(n-2)}(x)-f^{(n-2)}(a)\right]-f^{(n-1)}(a)(x-a). \end{align}\]

Combining the two results gives us:

\[f^{(n)}(c)\dfrac{(x-a)^2}{2}=f^{(n-2)}(x)-f^{(n-1)}(a)(x-a).\]

If we integrate once again, third time, we get on the left side:

\[\int_{a}^{x}f^{(n)}(c) \dfrac{(x-a)^2}{2}\cdot \Delta x = f^{(n)}(c)\dfrac{(x-a)^3}{3\cdot 2 \cdot 1} \;\;\; \text{or} \;\;\; f^{(n)}(c)\dfrac{(x-a)^3}{3!}. \]

On the right side we get:

\[\int_{a}^{x}f^{(n-2)}(x) \cdot \Delta x - \int_{a}^{x}f^{(n-2)}(a)\cdot \Delta x - \int_{a}^{x} f^{(n-1)}(a)(x-a)\cdot \Delta x \\ =\left[f^{(n-3)}(x)-f^{(n-3)}(a)\right]-f^{(n-2)}(a)\int_{a}^{x}1 \cdot \Delta x - f^{(n-1)}(a)\int_{a}^{x}(x-a) \cdot \Delta x \]

Combining the two sides:

\[f^{(n)}(c)\dfrac{(x-a)^3}{3!}=\left[f^{(n-3)}(x)- f^{(n-3)}(a) \right]-f^{(n-2)}(a)(x-a)- f^{(n-1)}(a)\dfrac{(x-a)^2}{2} . \]

Integrating this entire mass a fourth time, where we started with the function \(y=f^{(n)}(x)\), gives as you may have already guessed from the pattern:

\[ f^{(n)}(c)\dfrac{(x-a)^4}{4!}=\left[f^{(n-4)}(x)- f^{(n-4)}(a) \right]-f^{(n-3)}(a)\dfrac{(x-a)}{1!}- f^{(n-2)}(a)\dfrac{(x-a)^2}{2!}- f^{(n-1)}(a)\dfrac{(x-a)^3}{3!}.\]

By now the pattern should be clear. If we integrate \(n\) successive times to eventually find \(f(x)\) we arrive at a remarkable conclusion:

\[ f^{(n)}(c)\dfrac{(x-a)^n}{n!}=f(x)-f(a)-f'(a)\dfrac{(x-a)}{1!}-f''(a)\dfrac{(x-a)^2}{2!}-f'''(a)\dfrac{(x-a)^3}{3!} \dots \dots -f^{(n-2)}\dfrac{(x-a)^{(n-2)}}{(n-2)!} -f^{(n-1)}\dfrac{(x-a)^{(n-1)}}{(n-1)!} \]

which simplifies to:

\[f(x)=\sum_{k=0}^{n-1} f^{(k)}(a)\dfrac{(x-a)^k}{k!}+f^{(n)}(c)\dfrac{(x-a)^n}{n!}. \]

What this is saying is that any function can be expressed as a series of its \((n-1)\) derivatives, each evaluated at any point, \(a\), plus its \(n\)th derivative evaluated at a point between \(a\) and \(x\). Since the terms of the series are:

\[ f(x)=f(a)+f'(a)(x-a)+f''(a)\dfrac{(x-a)^2}{2!}+f'''(a)\dfrac{(x-a)^3}{3!}+ \dots \dots + f^{(n)}(c)\dfrac{(x-a)^n}{n!} .\]

One needs to not only know the value of \(f(x)\) at \(f(a)\) but also at \(f'(a)\), \(f''(a)\), \(f'''(a)\) etc... in order to find \(f(x)\),where \(x\), is any number other than \(a\).

The last term of the Taylor series differs slightly from its preceding terms. One needs to be able to calculate \(f^{(n)}(c)\dfrac{(x-a)^n}{n!}\) for a \(c\) somewhere in between \(a\) and \(x\).

In a faintly differentiable function such as \(f(x)=\dfrac{x^4}{8}\) the \(n\)th derivative is always a constant so that \(f^{(n)}(c)\) is that particular constant regardless of \(c\) in \(f^{(n)}(c)\). For example:

\[f(x)=\dfrac{x^4}{8}, \; f'(x)=\dfrac{x^3}{2}, \; f''(x)=\dfrac{3x^2}{2}, \; f'''(x)=3x, \;f^{(4)}(x)=3.\]

In this case, \(f^{(n)}(c)=f^{(4)}(x)=3\), which will always be 3 no matter what you input in the function. Remember \(n\)th derivative refers to the last derivative of the function.

In order to write or calculate a Taylor series for \(f(x)=\dfrac{x^4}{2}\) we first need to calculate its \(n\) -derivatives, which we have already done above. The Taylor Series is defined as:

\[\begin{align} f(x)&=\sum_{k=0}^{n-1}f^{(n)}(a)\dfrac{(x-a)^n}{n!}+f^{(n)}(c)\dfrac{(x-a)^n}{n!} \\ f(x)&=f(a)+f'(a)\dfrac{(x-a)!}{2!}+\dots + f^{(4)}(c)\dfrac{(x-a)^4}{4!} \\ \dfrac{x^4}{2}&=\dfrac{a^4}{2}+2a^3(x-a)+6a^2\dfrac{(x-a^2)}{2!}+12a\dfrac{(x-a)^3}{3!}+12\dfrac{(x-a)^4}{4!} . \end{align}\]

Simplifying it we get:

\[\dfrac{x^4}{2}=\dfrac{a^4}{2}+2a^3(x-a)+3a^2(x-a)^2+2a(x-a)^3+\dfrac{(x-a)^4}{12} . \]

The easiest number to choose for \(a\) is probably 1, though you can choose whatever number you want to for \(a\), so long as its \(n\) derivatives are all defined at \(a\).

Substituting \(a\) for 1 gives:

\[f(x)=\dfrac{x^4}{2}=\dfrac{1}{2}+2(x-1)+3(x-1)^2+2(x-1)^3+\dfrac{(x-1)^4}{2}.\]

Now let us evaluate \(f(x)\) at \(x=6\) using the Taylor Series:

\[\begin{align} f(6)&=\dfrac{6^4}{2}=\dfrac{1}{2}+2(5)+3(5)^2+2(5)^3+\dfrac{(5)^4}{2} \\ &=\dfrac{6^4}{2}=0.5+10+75+250+312.5 \\ &=\dfrac{1296}{2}=648\\ &=648 \end{align}\]

The sum of the series of terms corresponds exactly; however, as you can see, writing a Taylor Series for a faintly differentiable function is not a practical thing to do. For example in this series we had to calculate in the last term \(\dfrac{(5)^4}{2}\) in order to find \(f(6)\) or \(\dfrac{(6)^4}{2}\). Now if we were able to calculate \(5^4\) with ease then would it not be much easier to find \(6^4\) directly without having to go through a series of calculations and summations?

The answer is yes and thus the life of finite Taylor Series is short-lived.

Contributors and Attributions

• Faraz Hussain, Copied in whole or part from UnderstandingCalculus.com

• Integrated by Justin Marshall.