2.1: Domains of Holomorphy and Holomorphic Extensions

It turns out that not every domain in \(\mathbb{C}^n\) is a natural domain for holomorphic functions.

Definition: Domain of Holomorphy

Let \(U \subset \mathbb{C}^n\) be a domain\(^{1}\) (connected open set). The set \(U\) is a domain of holomorphy if there do not exist nonempty open sets \(V\) and \(W\), with \(V \subset U \cap W\), \(W \not\subset U\), and \(W\) connected, such that for every \(f \in \mathcal{O}(U)\) there exists an \(F \in \mathcal{O}(W)\) with \(f(z) = F(z)\) for all \(z \in V\). See Figure \(\PageIndex{1}\).

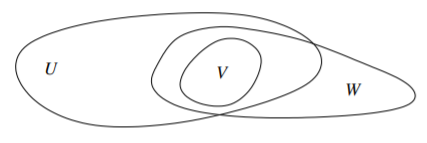
Figure \(\PageIndex{1}\)

The idea is that if a domain \(U\) is not a domain of holomorphy and \(V\), \(W\) exist as in the definition, then \(f\) “extends across the boundary” somewhere.

Example \(\PageIndex{1}\)

The unit ball \(\mathbb{B}_{n} \subset \mathbb{C}^n\) is a domain of holomorphy. Proof: Consider \(U=\mathbb{B}_{n}\), and suppose \(V\), \(W\) as in the definition exist. As \(W\) is connected and open, it is path connected. There exist points in \(W\) that are not in \(\mathbb{B}_{n}\), so there is a path \(\gamma\) in \(W\) that goes from a point \(q \in V\) to some \(p \in \partial \mathbb{B}_{n} \cap W\). Without loss of generality (after composing with rotations, that is, unitary matrices), assume \(p = (1,0,0,\ldots,0)\). Take the function \(f(z) = \frac{1}{1-z_1}\). The function \(F\) must agree with \(f\) on the component of \(\mathbb{B}_{n} \cap W\) that contains \(q\). But that component also contains \(p\) and so \(F\) must blow up (in particular it cannot be holomorphic) at \(p\). The contradiction shows that no \(V\) and \(W\) exist.

In one dimension this notion has no real content: Every domain in \(\mathbb{C}\) is a domain of holomorphy.

Exercise \(\PageIndex{1}\): (Easy)

In \(\mathbb{C}\), every domain is a domain of holomorphy.

Exercise \(\PageIndex{2}\)

If \(U_j \subset \mathbb{C}^n\) are domains of holomorphy (possibly an infinite set of domains), then the interior of \(\bigcap_{j} U_j\) is either empty or every connected component is a domain of holomorphy.

Exercise \(\PageIndex{3}\): (Easy)

Show that a polydisc in \(\mathbb{C}^n\) is a domain of holomorphy.

Exercise \(\PageIndex{4}\)

Suppose \(U_k \subset \mathbb{C}^{n_k}\), \(k=1,\ldots,\ell\) are domains of holomorphy, show that \(U_1 \times \cdots \times U_\ell\) is a domain of holomorphy. In particular every cartesian product of domains in \(\mathbb{C}\) is a domain of holomorphy.

Exercise \(\PageIndex{5}\)

1. Given \(p \in \partial \mathbb{B}_{n}\), find a function \(f\) holomorphic on \(\mathbb{B}_{n}\), \(C^\infty\)-smooth on \(\overline{\mathbb{B}_{n}}\) (all real partial derivatives of all orders extend continuously to \(\overline{\mathbb{B}_{n}}\)), that does not extend past \(p\) as a holomorphic function. Hint: For the principal branch of \(\sqrt{\cdot}\) the function \(\xi \mapsto e^{-1/\sqrt{\xi}}\) is holomorphic for \(\Re \xi > 0\) and extends to be continuous (even smooth) on all of \(\Re \xi \geq 0\).
2. Find a function \(f\) holomorphic on \(\mathbb{B}_{n}\) that does not extend past any point of \(\partial \mathbb{B}_{n}\).

Various notions of convexity will play a big role later on. A set \(S\) is geometrically convex if \(t x + (1-t)y \in S\) for all \(x,y \in S\) and \(t \in [0,1]\). The exercise below says that every geometrically convex domain is a domain of holomorphy. Domains of holomorphy are often not geometrically convex (e.g. any domain in \(\mathbb{C}\) is a domain of holomorphy), so classical convexity is not the correct notion, but it is in the right direction.

Exercise \(\PageIndex{6}\)

Show that a geometrically convex domain in \(\mathbb{C}^n\) is a domain of holomorphy.

In the following when we say \(f \in \mathcal{O}(U)\) extends holomorphically to \(V\) where \(U \subset V\), we mean that there exists a function \(F \in \mathcal{O}(V)\) such that \(f = F\) on \(U\).

Remark \(\PageIndex{1}\)

The subtlety of the definition of a domain of holomorphy is that it does not necessarily talk about functions extending to a larger set, since we must take into account single-valuedness. For instance, let \(f\) be the principal branch of the logarithm defined on the slit plane \(U = \mathbb{C} \setminus \{ z \in \mathbb{C} : \Im z = 0, \Re z \leq 0 \}\). We can locally define an extension from one side through the boundary of the domain, but we cannot define an extension on a open set that contains \(U\). This example should be motivation for why we let \(V\) be a proper subset of \(U \cap W\), and why \(W\) need not include all of \(U\). This one dimensional intuition can be extended to an actual example in \(\mathbb{C}^n\), see Exercise \(\PageIndex{14}\).

In dimension two or more, not every domain is a domain of holomorphy. We have the following theorem. The domain \(H\) in the theorem is called the Hartogs figure.

Theorem \(\PageIndex{1}\)

Let \((z,w) = (z_1,\ldots,z_m,w_{1},\ldots,w_{k}) \in \mathbb{C}^m \times \mathbb{C}^k\) be the coordinates. For two numbers \(0 < a,b < 1\), define the set \(H \subset \mathbb{D}^{m+k}\) by \[\begin{align}\begin{aligned} H = \bigl\{ (z,w) \in \mathbb{D}^{m+k} : |z_j| > a ~\text{for $j=1,\ldots,m$} \bigr\} \\ \cup \bigl\{ (z,w) \in \mathbb{D}^{m+k} : |w_j| < b ~\text{for $j=1,\ldots,k$} \bigr\} .\end{aligned}\end{align}\] If \(f \in \mathcal{O}(H)\), then \(f\) extends holomorphically to \(\mathbb{D}^{m+k}\).

In \(\mathbb{C}^2\) if \(m=1\) and \(k=1\), see (the \(c\) will come up in the proof).

Figure \(\PageIndex{2}\)

Proof

Pick a \(c \in (a,1)\). Let \[\Gamma = \bigl\{ z \in \mathbb{D}^{m} : |z_j| = c ~\text{for $j=1,\ldots,m$ } \bigr\}.\] That is, \(\Gamma\) is the distinguished boundary of \(c \mathbb{D}^m\), a polydisc centered at 0 of radius \(c\) in \(\mathbb{C}^m\). Define the function \[F(z,w) = \frac{1}{{(2\pi i)}^m} \int_\Gamma \frac{f(\xi,w)}{\xi-z} \, d\xi .\] Clearly, \(F\) is well-defined on \[c\mathbb{D}^m \times \mathbb{D}^k\] as \(\xi\) only ranges through \(\Gamma\) and so as long as \(w \in \mathbb{D}^k\) then \((\xi,w) \in H\).

The function \(F\) is holomorphic in \(w\) as we can differentiate underneath the integral and \(f\) is holomorphic in \(w\) on \(H\). Furthermore, \(F\) is holomorphic in \(z\) as the kernel \(\frac{1}{\xi-z}\) is holomorphic in \(z\) as long as \(z \in c\mathbb{D}^m\).

For any fixed \(w\) with \(|w_j| < b\) for all \(j\), the Cauchy integral formula says \(F(z,w) = f(z,w)\) for all \(z \in c \mathbb{D}^m\). Hence, \(F=f\) on the open set \(c\mathbb{D}^m \times b\mathbb{D}^k\), and so they are equal on \((c\mathbb{D}^m \times \mathbb{D}^k) \cap H\). Combining \(F\) and \(f\) we obtain a holomorphic function on \(\mathbb{D}^{m+k}\) that extends \(f\).

The theorem is used in many situations to extend holomorphic functions. We usually need to translate, scale, rotate (apply a unitary matrix), and even take more general biholomorphic mappings of \(H\), to place it wherever we need it. The corresponding polydisc—or the image of the polydisc under the appropriate biholomorphic mapping if one was used—to which all holomorphic functions on \(H\) extend is denoted by \(\widehat{H}\) and is called the hull of \(H\).

Let us state a simple but useful case of the so-called Hartogs phenomenon.

Corollary \(\PageIndex{1}\)

Let \(U \subset \mathbb{C}^n\), \(n \geq 2\), be an open set and \(p \in U\). Then every \(f \in \mathcal{O}\bigl(U \setminus \{ p \} \bigr)\) extends holomorphically to \(U\).

Proof

Without loss of generality, by translating and scaling (those operations are after all holomorphic), we assume that \(p = \bigl(0,\ldots,0,\frac{3}{4}\bigr)\) and the unit polydisc \(\mathbb{D}^n\) is contained in \(U\). We fit a Hartogs figure \(H\) in \(U\) by letting \(m=n-1\) and \(k=1\), writing \(\mathbb{C}^n = \mathbb{C}^{n-1} \times \mathbb{C}^{1}\), and taking \(a = b = \frac{1}{2}\). Then \(H \subset U\), and \(p \in \mathbb{D}^n \setminus H\). Theorem \(\PageIndex{1}\) says that \(f\) extends to be holomorphic at \(p\).

This result provides another reason why holomorphic functions in several variables have no isolated zeros (or poles). Suppose \(U \subset \mathbb{C}^n\), \(n \geq 2\), and \(f \in \mathcal{O}(U)\) with \(f\) being zero only at \(p\), that is \(f^{-1}(0) = \{ p \}\). Then \(\frac{1}{f}\) would be holomorphic in \(U \setminus \{ p \}\). It would not be possible to extend \(f\) through \(p\) (not even continuously let alone holomorphically), and we obtain a contradiction.

The extension works in an even more surprising fashion. We could take out a very large set, for example, any geometrically convex subset:

Exercise \(\PageIndex{7}\)

Suppose \(U \subset \mathbb{C}^n\), \(n \geq 2\), be an open set and \(K \subset \subset U\) is a compact geometrically convex subset. If \(f \in \mathcal{O}(U \setminus K)\), then \(f\) extends to be holomorphic in \(U\). Hint: Find a nice point on \(\partial K\) and try extending a little bit. Then make sure your extension is single-valued.

Convexity of \(K\) is not needed; we only need that \(U\setminus K\) is connected, however, the proof is much harder. The single-valuedness of the extension is the key point that makes the general proof harder.

Notice the surprising fact that every holomorphic function on the shell \[\mathbb{B}_{n} \setminus \overline{B_{1-\epsilon}(0)} = \bigl\{ z \in \mathbb{C}^n : 1-\epsilon < ||z|| < 1 \bigr\}\] for any \(\epsilon > 0\) automatically extends to a holomorphic function of \(\mathbb{B}_{n}\). We need \(n > 1\). The extension result decisively does not work in one dimension; for example take \(\frac{1}{z}\). There is a related fact about zero sets. If \(n \geq 2\) and \(f \in \mathcal{O}(\mathbb{B}_{n})\) the set of its zeros must “touch the boundary” (in other words \(f^{-1}(0)\) is not compact) or be empty: If the set of zeros were compact in \(\mathbb{B}_{n}\), then we could try to extend the function \(\frac{1}{f}\).

Exercise \(\PageIndex{8}\)

Let \[T = \bigl\{ (z_1,z_2) \in \mathbb{D}^2 : |z_2| < |z_1| \bigr\} .\] Show that \(T\) is a domain of holomorphy. Then show that if \[\widetilde{T} = T \cup B_{\epsilon}(0)\] for an arbitrarily small \(\epsilon > 0\), then \(\widetilde{T}\) is not a domain of holomorphy. In fact, every function holomorphic on \(\widetilde{T}\) extends to a holomorphic function of \(\mathbb{D}^2\).

Exercise \(\PageIndex{9}\)

Take the natural embedding of \(\mathbb{R}^2 \subset \mathbb{C}^2\). Suppose \(f \in \mathcal{O}(\mathbb{C}^2 \setminus \mathbb{R}^2)\). Show that \(f\) extends holomorphically to all of \(\mathbb{C}^2\). Hint: Change coordinates before using Hartogs.

Exercise \(\PageIndex{10}\)

Suppose \[U = \bigl\{ (z,w) \in \mathbb{D}^2 : \frac{1}{2} < |z| \bigr\} .\] Draw \(U\). Let \(\gamma = \bigl\{ z \in \mathbb{C} : |z| = \frac{3}{4} \bigr\}\) oriented positively. If \(f \in \mathcal{O}(U)\), then show that the function \[F(z,w) = \frac{1}{2\pi i} \int_\gamma \frac{f(\xi,w)}{\xi-z} \, d\xi\] is well-defined in \(\bigl( (\frac{3}{4}) \mathbb{D} \bigr) \times \mathbb{D}\), holomorphic where defined, yet it is not necessarily true that \(F = f\) on the intersections of their domains.

Exercise \(\PageIndex{11}\)

Suppose \(U \subset \mathbb{C}^n\) is an open set such that for every \(z \in \mathbb{C}^n \setminus \{ 0 \}\), there is a \(\lambda \in \mathbb{C}\) such that \(\lambda z \in U\). Let \(f \colon U \to \mathbb{C}\) be holomorphic with \(f(\lambda z) = f(z)\) whenever \(z \in U\), \(\lambda \in \mathbb{C}\) and \(\lambda z \in U\).

1. (easy) Prove that \(f\) is constant.
2. (hard) Relax the requirement on \(f\) to being meromorphic: \(f = \frac{g}{h}\) for holomorphic \(g\) and \(h\). Find a nonconstant example, and prove that such an \(f\) must be rational (that is, \(g\) and \(h\) must be polynomials).

Exercise \(\PageIndex{12}\)

Suppose \[U = \bigl\{ z \in \mathbb{D}^3 : \frac{1}{2} < |z_1| \quad\text{or}\quad \frac{1}{2} < |z_2| \bigr\} . \] Prove that every function \(f \in \mathcal{O}(U)\) extends to \(\mathbb{D}^3\). Compare to Exercise \(\PageIndex{10}\).

Exercise \(\PageIndex{13}\)

Suppose \(U = \mathbb{C}^n \setminus \{ z \in \mathbb{C}^n : z_1 = z_2 = 0 \}\), \(n \geq 2\). Show that every \(f \in \mathcal{O}(U)\) extends holomorphically to \(\mathbb{C}^n\).

Exercise \(\PageIndex{14}\)

Construct an example domain \(U \subset \mathbb{C}^2\) that is not a domain of holomorphy, but such that there is no domain \(W \subset \mathbb{C}^2\) with \(U \subset W\) such that every \(f \in \mathcal{O}(U)\) extends to \(W\). Hint: Extending the example from will almost give you a \(U\), but it will be a domain of holomorphy, you need to modify it a little bit.

Example \(\PageIndex{2}\)

By Exercise \(\PageIndex{9}\), \(U_1 = \mathbb{C}^2 \setminus \mathbb{R}^2\) is not a domain of holomorphy. On the other hand, \(U_2 = \mathbb{C}^2 \setminus \{ z \in \mathbb{C}^2 : z_2 = 0 \}\) is a domain of holomorphy; simply use \(f(z) = \frac{1}{z_2}\) as the function that cannot extend. Therefore, \(U_1\) and \(U_2\) are rather different as far as complex variables are concerned, yet they are the same set if we ignore the complex structure. They are both simply a 4-dimensional real vector space minus a 2-dimensional real vector subspace. That is, \(U_1\) is the set where either \(\Im z_1 \not= 0\) or \(\Im z_2 \not= 0\), while \(U_2\) is the set where either \(\Re z_2 \not= 0\) or \(\Im z_2 \not= 0\).

The condition of being a domain of holomorphy, requires something more than just some real geometric condition on the set. Namely, we have shown that the image of a domain of holomorphy via an orthonormal real-linear mapping (so preserving distances, angles, straight lines, etc.) need not be a domain of holomorphy. Therefore, when we want to “rotate” in complex analysis we need to use a complex linear mapping, so a unitary matrix.

Footnotes

[1] Domain of holomorphy can make sense for disconnected sets (not domains), and some authors do define it so.