3.4: Extension of CR Functions

We will apply the so-called “technique of analytic discs” together with Baouendi–Trèves to prove the Lewy extension theorem. Lewy’s original proof was different and predates Baouendi–Trèves. A local extension theorem of this type was first proved by Helmut Knesser in 1936.

Theorem \(\PageIndex{1}\)

Suppose \(M \subset \mathbb{C}^n\) is a smooth real hypersurface and \(p \in M\). There exists a neighborhood \(U\) of \(p\) with the following property. Suppose \(r \colon U \to \mathbb{R}\) is a smooth defining function for \(M \cap U\), denote by \(U_- \subset U\) the set where \(r\) is negative and \(U_+ \subset U\) the set where \(r\) is positive. Let \(f \colon M \to \mathbb{R}\) be a smooth CR function. Then:

1. If the Levi form with respect to \(r\) has a positive eigenvalue at \(p\), then \(f\) extends to a holomorphic function on \(U_-\) continuous up to \(M\) (that is, continuous on \(\{ z \in U : r(z) \leq 0 \}\)).
2. If the Levi form with respect to \(r\) has a negative eigenvalue at \(p\), then \(f\) extends to a holomorphic function on \(U_+\) continuous up to \(M\) (that is, continuous on \(\{ z \in U : r(z) \geq 0 \}\)).
3. If the Levi form with respect to \(r\) has eigenvalues of both signs at \(p\), then \(f\) extends to a function holomorphic on \(U\).

So if the Levi form has eigenvalues of both signs, then near \(p\) all CR functions are restrictions of holomorphic functions. The function \(r\) can be any defining function for \(M\). Either we can extend it to all of \(U\) or we could take a smaller \(U\) such that \(r\) is defined on \(U\). As we noticed before, once we pick sides (where \(r\) is positive and where it is negative), then the number of positive eigenvalues and the number of negative eigenvalues of the Levi form is fixed. A different \(r\) may flip \(U_-\) and \(U_+\), but the conclusion of the theorem is exactly the same.

Proof

We prove the first item, and the second item follows by considering \(-r\). Suppose \(p = 0\) and \(M\) is given in some neighborhood \(\Omega\) of the origin as \[\Im w = |z_1|^2 + \sum_{j=2}^{n-1} \epsilon_j |z_j|^2 + E(z_1,z',\bar{z}_1,\bar{z}',\Re w) ,\] where \(z' = (z_2,\ldots,z_{n-1})\), \(\epsilon_j = -1,0,1\), and \(E\) is \(O(3)\). Let \(\Omega_-\) be given by \[0 > r = |z_1|^2 + \sum_{j=2}^{n-1} \epsilon_j |z_j|^2 + E(z_1,z',\bar{z}_1,\bar{z}',\Re w) - \Im w .\] The (real) Hessian of the function \[z_1 \mapsto |z_1|^2 + E(z_1,0,\bar{z}_1,0,0)\] is positive definite in a neighborhood of the origin and the function has a strict minimum at 0. There is some small disc \(D \subset \mathbb{C}\) such that this function is strictly positive on \(\partial D\).

Therefore, for \((z',w) \in W\) in some small neighborhood \(W \subset \mathbb{C}^{n-1}\) of the origin, the function \[z_1 \mapsto |z_1|^2 + \sum_{j=2}^n \epsilon_j |z_j|^2 + E(z_1,z',\bar{z}_1,\bar{z}',\Re w) - \Im w\] is still strictly positive on \(\partial D\).

We wish to apply Baouendi–Trèves and so let \(K\) be the compact neighborhood of the origin from the theorem. Take \(D\) and \(W\) small enough such that \((D \times W) \cap M \subset K\). Find the polynomials \(p_j\) that approximate \(f\) uniformly on \(K\). Consider \(z_1 \in D\) and \((z',w) \in W\) such that \((z_1,z',w) \in \Omega_-\). Let \(\Delta = \bigl( D \times \{ (z',w) \} \bigr) \cap \Omega_-\). Denote by \(\partial \Delta\) the boundary of \(\Delta\) in the subspace topology of \(\mathbb{C} \times \{ (z',w) \}\).

The set \(\Omega_+\) where \(r > 0\) is open and it contains \((\partial D) \times \{ (z',w) \}\). Therefore, \(\partial \Delta\) contains no points of \((\partial D) \times \{ (z',w) \}\). Consequently, \(\partial \Delta\) contains only points where \(r = 0\), that is \(\partial \Delta \subset M\), and also \(\partial \Delta \subset D \times W\). As \((D \times W) \cap M \subset K\), we have \(\partial \Delta \subset K\). See Figure \(\PageIndex{1}\).

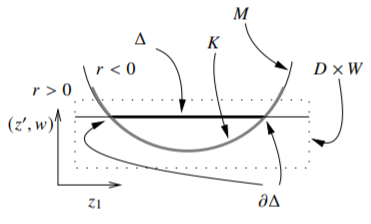
Figure \(\PageIndex{1}\)

As \(p_j \to f\) uniformly on \(K\), then \(p_j \to f\) uniformly on \(\partial \Delta\). As \(p_j\) are holomorphic, then by the maximum principle, \(p_j\) converge uniformly on all of \(\Delta\). In fact, as \((z_1,z',w)\) was an arbitrary point in \((D \times W) \cap \Omega_-\), the polynomials \(p_j\) converge uniformly on \((D \times W) \cap \overline{\Omega_-}\). Let \(U = D \times W\), then \(U_- = (D \times W) \cap \Omega_-\). Notice \(U\) depends on \(K\), but not on \(f\). So \(p_j\) converge to a continuous function \(F\) on \(\overline{U_-} \cap U\) and \(F\) is holomorphic on \(U_-\). Clearly \(F\) equals \(f\) on \(M \cap U\).

To prove the last item, pick a side, and then use one of the first two items to extend the function to that side. Via the tomato can principle (Theorem 2.3.2) the function also extends across \(M\) and therefore to a whole neighborhood of \(p\).

If you were wondering what happened to the analytic discs we promised, the \(\Delta\) in the above is an analytic disc (simply connected) for a small enough \(U\), but it was not necessary to prove that fact.

We state the next corollary for a strongly convex domain, even though it holds with far more generality. It is a simpler version of the Hartogs-Bochner\(^{1}\). Later, in Exercise 4.3.4, you will prove it for strongly pseudoconvex domains. However, the theorem is true for every bounded domain with connected smooth boundary with no assumptions on the Levi form, but a different approach would have to be taken.

Corollary \(\PageIndex{1}\)

Suppose \(U \subset \mathbb{C}^n\), \(n \geq 2\), is a bounded domain with smooth boundary that is strongly convex and \(f \colon \partial U \to \mathbb{C}\) is a smooth CR function, then there exists a continuous function \(F \colon \overline{U} \to \mathbb{C}\) holomorphic in \(U\) such that \(F|_{\partial U} = f\).

Proof

A strongly convex domain is strongly pseudoconvex, so \(f\) must extend to the inside locally near every point. The extension is locally unique as any two extensions have the same boundary values. Therefore, there exists a set \(K \subset \subset U\) such that \(f\) extends to \(U \setminus K\). Via an exercise below we can assume that \(K\) is strongly convex and therefore we can apply the special case of Hartogs phenomenon that you proved in Exercise 2.1.6 to find an extension holomorphic in \(U\).

Exercise \(\PageIndex{1}\)

Prove the existence of the strongly convex \(K\) in the proof of Corollary \(\PageIndex{1}\) above.

Exercise \(\PageIndex{2}\)

Show by example that the corollary is not true when \(n=1\). Explain where in the proof have we used that \(n \geq 2\).

Exercise \(\PageIndex{3}\)

Suppose \(f \colon \partial \mathbb{B}_{2} \to \mathbb{C}\) is a smooth CR function. Write down an explicit formula for the extension \(F\).

Exercise \(\PageIndex{4}\)

A smooth real hypersurface \(M \subset \mathbb{C}^3\) is defined by \(\Im w = |z_1|^2-|z_2|^2 + O(3)\) and \(f\) is a real-valued smooth CR function on \(M\). Show that \(|f|\) does not attain a maximum at the origin.

Exercise \(\PageIndex{5}\)

A real-analytic hypersurface \(M \subset \mathbb{C}^n\), \(n \geq 3\), is such that the Levi form at \(p \in M\) has eigenvalues of both signs. Show that every smooth CR function \(f\) on \(M\) is, in fact, real-analytic in a neighborhood of \(p\).

Exercise \(\PageIndex{6}\)

Let \(M \subset \mathbb{C}^3\) be defined by \(\Im w = |z_1|^2-|z_2|^2\).

1. Show that for this \(M\), the conclusion of Baouendi–Trèves holds with an arbitrary compact subset \(K \subset \subset M\).
2. Use this to show that every smooth CR function \(f \colon M \to \mathbb{C}\) is a restriction of an entire holomorphic function \(F \colon \mathbb{C}^3 \to \mathbb{C}\).

Exercise \(\PageIndex{7}\)

Find an \(M \subset \mathbb{C}^n\), \(n \geq 2\), such that near some \(p \in M\), for every neighborhood \(W\) of \(p\) in \(M\), there is a CR function \(f \colon W \to \mathbb{C}\) that does not extend holomorphically to either side of \(M\) at \(p\).

Exercise \(\PageIndex{8}\)

Suppose \(f \colon \partial \mathbb{B}_{n} \to \mathbb{C}\) is a smooth function and \(n \geq 2\). Prove that \(f\) is a CR function if and only if \[\int_0^{2\pi} f(e^{i\theta}v) \, e^{ik\theta} d\theta = 0 \qquad \text{for all $v \in \partial \mathbb{B}_{n}$ and all $k \in \mathbb{N}$.}\]

Exercise \(\PageIndex{9}\)

Prove the third item in the Lewy extension theorem without the use of the tomato can principle. That is, prove in a more elementary way that if \(M \subset U \subset \mathbb{C}^n\) is a smooth real hypersurface in an open set \(U\) and \(f \colon U \to \mathbb{C}\) is continuous and holomorphic in \(U \setminus M\), then \(f\) is holomorphic.

Studying solutions to nonhomogeneous CR equations of the form \(X f = \psi\) for a CR vector field \(X\), and the fact that such conditions can guarantee that a function must be real-analytic, led Lewy to a famous, very surprising, and rather simple example of a linear partial differential equation with smooth coefficients that has no solution on any open set\(^{2}\). The example is surprising because when a linear PDE has real-analytic coefficients, a solution always exists by the theorem of Cauchy–Kowalevski. Furthermore, if \(X\) is a real vector field (\(X\) is in \(TM\) not in \(\mathbb{C} \otimes TM\)), then a solution to \(Xf = \psi\) exists by the method of characteristics, even if \(X\) and \(\psi\) are only smooth.

Footnotes

[1] What is called Hartogs–Bochner is the \(C^1\) version of this theorem where the domain is only assumed to be bounded and the boundary connected, and it was proved by neither Hartogs nor Bochner, but by Martinelli in 1961.

[2] Lewy, Hans, An example of a smooth linear partial differential equation without solution, Annals of Mathematics, 66 (1957), 155–158.