3.3: Approximation of CR Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
The following theorem (proved circa 1980) holds in much more generality, but we state its simplest version. One of the simplifications we make is that we consider only smooth CR functions here, although the theorem holds even for continuous CR functions where the CR conditions are interpreted in the sense of distributions.
Baouendi–Trèves
Suppose M⊂Cn is a smooth real hypersurface, p∈M is a point, and z=(z1,…,zn) are the holomorphic coordinates of Cn. Then there exists a compact neighborhood K⊂M of p, such that for every smooth CR function f:M→C, there exists a sequence {pj} of polynomials in z such that pj(z)→f(z)uniformly in K.
A key point is that K cannot be chosen arbitrarily, it depends on p and M. On the other hand it does not depend on f. Given M and p∈M there is a K such that every CR function on M is approximated uniformly on K by holomorphic polynomials. The theorem applies in one dimension, although in that case the theorem of Mergelyan (see Theorem B.31) is much more general.
Let us show that K cannot possibly be arbitrary. For simplicity n=1. Let S1⊂C be the unit circle (boundary of the disc), then every smooth function on S1 is a smooth CR function. Let f be a nonconstant real function such as ℜz. Suppose for contradiction that we could take K=S1 in the theorem. Then f(z)=ℜz could be uniformly approximated on S1 by holomorphic polynomials. By the maximum principle, the polynomials would converge on D to a holomorphic function on D continuous on ¯D. This function would have nonconstant real boundary values, which is impossible. Clearly K cannot be the entire circle.
The example is easily extended to Cn by considering M=S1×Cn−1, then ℜz1 is a smooth CR function on M that cannot be approximated uniformly on S1×{0} by holomorphic polynomials.
The technique of the example above will be used later in a more general situation, to extend CR functions using Baouendi–Trèves.
It is important to note the difference between Baouendi–Trèves (and similar theorems in complex analysis) and the Weierstrass approximation theorem. In Baouendi–Trèves we obtain an approximation by holomorphic polynomials, while Weierstrass gives us polynomials in the real variables, or in z and ˉz. For example, via Weierstrass, every continuous function is uniformly approximable on S1 via polynomials in ℜz and ℑz, and therefore by polynomials in z and ˉz. These polynomials do not in general converge anywhere but on S1.
Let z=x+iy as usual in C. Find a sequence of polynomials in x and y that converge uniformly to ex−y on S1, but diverge everywhere else.
The proof is an ingenious use of the standard technique used to prove the Weierstrass approximation theorem. Also, as we have seen mollifiers before, the technique will not be completely foreign even to the reader who does not know the Weierstrass approximation theorem. Basically what we do is use the standard convolution argument, this time against a holomorphic function. Letting z=x+iy we only do the convolution in the x variables keeping y=0. Then we use the fact that the function is CR to show that we get an approximation even for other y.
In the formulas below, given a vector v=(v1,…,vn), it will be useful to write [v]2def=v21+⋯+v2n.
The following lemma is a neat application of ideas from several complex variables to solve a problem that does not at first seems to involve holomorphic functions.
Let W be the set of n×n complex matrices A such that ||(ℑA)x||<||(ℜA)x|| for all nonzero x∈Rn and ℜA is positive definite. Then for all A∈W, ∫Rne−[Ax]2detAdx=πn/2.
- Proof
-
Suppose A has real entries and A is positive definite (so A is also invertible). By a change of coordinates ∫Rne−[Ax]2detAdx=∫Rne−[x]2dx=(∫Re−x21dx1)⋯(∫Re−x2ndxn)=(√π)n. Next suppose A is any matrix in W. There is some ϵ>0 such that ||(ℑA)x||2≤(1−ϵ2)||(ℜA)x||2 for all x∈Rn. That is because we only need to check this for x in the unit sphere, which is compact (exercise). By reality of ℜA, ℑA, and x we get [(ℜA)x]2=||(ℜA)x||2 and [(ℑA)x]2=||(ℑA)x||2. So |e−[Ax]2|=e−ℜ[Ax]2≤e−[(ℜA)x]2+[(ℑA)x]2≤e−ϵ2[(ℜA)x]2. Therefore, the integral exists for all A in W by a similar computation as above.
The expression ∫Rne−[Ax]2detAdx is a well-defined holomorphic function in the entries of A, thinking of W as a domain (see exercises below) in Cn2. We have a holomorphic function that is constantly equal to πn/2 on W∩Rn2 and hence it is equal to πn/2 everywhere on W.
Prove the existence of ϵ>0 in the proof above.
Show that W⊂Cn2 in the proof above is a domain (open and connected).
Prove that we can really differentiate under the integral to show that the integral is holomorphic in the entries of A.
Show that some hypotheses are needed for the lemma. In particular, take n=1 and find the exact set of A (now a complex number) for which the conclusion of the lemma is true.
Given an n×n matrix A, let ||A|| denote the operator norm, ||A||=sup||v||=1||Av||=supv∈Cn,v≠0||Av||||v||.
Let W be as in Lemma 3.3.1. Let B be an n×n real matrix such that ||B||<1. Show that I+iB∈W.
We will be using differential forms, and the following lemma says that as far as the exterior derivative is concerned, all CR functions behave as restrictions of holomorphic functions.
Let M⊂Cn be a smooth real hypersurface, f:M→C be a smooth CR function, and (z1,…,zn) be the holomorphic coordinates of Cn. Then at each point p∈M, the exterior derivative df is a linear combination of dz1,…,dzn, thinking of z1,…,zn as functions on M.Namely, d(fdz)=df∧dz=0.
Recall the notation dz=dz1∧dz2∧⋯∧dzn.
- Proof
-
After a complex affine change of coordinates, we simply need to prove the result at the origin. Let ξ1,…,ξn be the new holomorphic coordinates and suppose the T(1,0)0M tangent space is spanned by ∂∂ξ1|0,…,∂∂ξn−1|0, and such that ∂∂ℜξn|0 is tangent and ∂∂ℑξn|0 is normal. At the origin, the CR conditions are ∂f∂ˉξk(0)=0 for all k, so df(0)=∂f∂ξ1(0)dξ1(0)+⋯+∂f∂ξn−1(0)dξn−1(0)+∂f∂ℜξn(0)d(ℜξn)(0). Also, at the origin dξn(0)=d(ℜξn)(0)+id(ℑξn)(0)=d(ℜξn)(0). So df(0) is a linear combination of dξ1(0),…,dξn(0). As ξ is a complex affine function of z, then each dξk is a linear combination of dz1 through dzn, and the claim follows. So if f is a CR function, then d(fdz)=df∧dz=0 since dzk∧dzk=0.
Proof of the theorem of Baouendi–Trèves. Suppose M⊂Cn is a smooth real hypersurface, and without loss of generality suppose p=0∈M. Let z=(z1,…,zn) be the holomorphic coordinates, write z=x+iy, y=(y′,yn), and suppose M is given by yn=ψ(x,y′), where ψ is O(2). The variables (x,y′) parametrize M near 0: zj=xj+iyj, for j=1,…,n−1,andzn=xn+iψ(x,y′). Define φ(x,y′)=(y1,…,yn−1,ψ(x,y′)). Write (x,y′)↦z=x+iφ(x,y′) as the parametrization. That is, think of z as a function of (x,y′).
Let r>0 and d>0 be small numbers to be determined later. Assume they are small enough so that f and φ are defined and smooth on some neighborhood of the set where ||x||≤r and ||y′||≤d.
There exists a smooth g:Rn→[0,1] such that g≡1 on Br/2(0) and g≡0 outside of Br(0). See Figure 3.3.1. Explicit formula can be given. Alternatively we obtain such a g by use of mollifiers on a function that is identically one on B3r/4(0) and zero elsewhere. Such a g is commonly called a cutoff function.
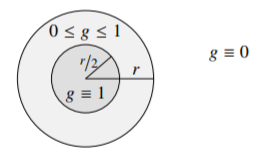
Figure 3.3.1
Find an explicit formula for g without using mollifiers.
Let K′={(x,y′):||x||≤r4,||y′||≤d}. Let K=z(K′), that is the image of K′ under the mapping z(x,y′).
Consider the CR function f a function of (x,y′) and write f(x,y′). For ℓ∈N, let αℓ be a differential n-form defined (thinking of w∈Cn as a constant parameter) by αℓ(x,y′)=(ℓπ)n/2e−ℓ[w−z]2g(x)f(x,y′)dz=(ℓπ)n/2e−ℓ[w−x−iφ(x,y′)]2g(x)f(x,y′)(dx1+idy1)∧⋯∧(dxn−1+idyn−1)∧(dxn+idψ(x,y′)).
The key is the exponential, which looks like the bump function mollifier, except that now we have w and z possibly complex. The exponential is also holomorphic in w, and that will give us entire holomorphic approximating functions.
Fix y′ with 0<||y′||<d and let D be defined by D={(x,s)∈Rn×Rn−1:||x||<r and s=ty′ for t∈(0,1)}. D is an (n+1)-dimensional “cylinder.” We take a ball in the x directions, then take a single fixed point y′ in the s variables and make a cylinder. See Figure 3.3.2.
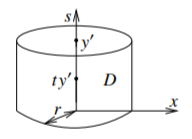
Figure 3.3.2
Orient D in the standard way as if it sat in the (x,t) variables in Rn×R. Stokes’ theorem says ∫Ddαℓ(x,s)=∫∂Dαℓ(x,s). Since g(x)=0 if ||x||≥r, αℓ is zero on the sides of the cylinder D, so the integral over ∂D only needs to consider the top and bottom of the cylinder. And because of g, the integral over the top and bottom can be taken over Rn. As is usual in these sorts of arguments, we do the slight abuse of notation where we ignore that f and φ are undefined where g is identically zero:
∫∂Dαℓ(x,s)=(ℓπ)n/2∫x∈Rne−ℓ[w−x−iφ(x,y′)]2g(x)f(x,y′)dx1∧⋯∧dxn−1∧(dxn+idxψ(x,y′))−(ℓπ)n/2∫x∈Rne−ℓ[w−x−iφ(x,0)]2g(x)f(x,0)dx1∧⋯∧dxn−1∧(dxn+idxψ(x,0)), where dx means the derivative in the x directions only. That is, dxψ=∂ψ∂x1dx1+⋯+∂ψ∂xndxn.
We will show that as ℓ→∞, the left-hand side of (3.3.19) goes to zero uniformly for w∈K and the first term on the right-hand side goes to f(˜x,y′) if w=z(˜x,y′) is in M. Hence, we define entire functions that we will show approximate f: fℓ(w)=(ℓπ)n/2∫x∈Rne−ℓ[w−x−iφ(x,0)]2g(x)f(x,0)dx1∧⋯∧dxn−1∧(dxn+idxψ(x,0)). Clearly each fℓ is holomorphic and defined for all w∈Cn.
In the next claim it is important that f is a CR function.
We have dαℓ(x,s)=(ℓπ)n/2e−ℓ[w−z(x,s)]2f(x,s)dg(x)∧dz(x,s), and for sufficiently small r>0 and d>0, limℓ→∞(ℓπ)n/2∫(x,s)∈De−ℓ[w−z(x,s)]2f(x,s)dg(x)∧dz(x,s)=0 uniformly as a function of w∈K and y′∈Bd(0) (recall that D depends on y′).
- Proof
-
The function (x,s)↦e−ℓ[w−z(x,s)]2 is CR (as a function on M), and so is f(x,s). Therefore, using Lemma 3.3.2, dαℓ(x,s)=(ℓπ)n/2e−ℓ[w−z(x,s)]2f(x,s)dg(x)∧dz(x,s). Since dg is zero for ||x||≤r2, the integral ∫Ddαℓ(x,s)=(ℓπ)n/2∫De−ℓ[w−z(x,s)]2f(x,s)dg(x)∧dz(x,s) is only evaluated for the subset of D where ||x||>r2.
Suppose w∈K and (x,s) \in D with ||x|| > \frac{r}{2}. Let w = z(\tilde{x},\tilde{s}). We need to estimate \left|e^{ -\ell {[w - z(x,s)]}^2 }\right| = e^{ -\ell \Re {[w - z(x,s)]}^2 } . Then -\Re {[w - z]}^2 = -||\tilde{x}-x||^2 + ||\varphi(\tilde{x},\tilde{s})-\varphi(x,s)||^2 . By the mean value theorem ||\varphi(\tilde{x},\tilde{s})-\varphi(x,s)|| \leq ||\varphi(\tilde{x},\tilde{s})-\varphi(x,\tilde{s})|| + ||\varphi(x,\tilde{s})-\varphi(x,s)|| \leq a ||\tilde{x}-x|| + A ||\tilde{s}-s|| , where a and A are a = \sup_{||\hat{x}|| \leq r, ||\hat{y}'|| \leq d} \left| \left| \,\left[\frac{\partial \varphi}{\partial x}(\hat{x},\hat{y}')\right]\, \right| \right| , \qquad A = \sup_{||\hat{x}|| \leq r, ||\hat{y}'|| \leq d} \left| \left| \,\left[\frac{\partial \varphi}{\partial y'}(\hat{x},\hat{y}'))\right]\,\right| \right| . Here \bigl[ \frac{\partial \varphi}{\partial x} \bigr] and \bigl[ \frac{\partial \varphi}{\partial y'} \bigr] are the derivatives (matrices) of \varphi with respect to x and y' respectively, and the norm we are taking is the operator norm. Because \bigl[ \frac{\partial \varphi}{\partial x} \bigr] is zero at the origin, we pick r and d small enough (and hence K small enough) so that a \leq \frac{1}{4}. We furthermore pick d possibly even smaller to ensure that d \leq \frac{r}{32A}. We have that \frac{r}{2} \leq ||x|| \leq r, but ||\tilde{x}|| \leq \frac{r}{4} (recall w \in K), so \frac{r}{4} \leq ||\tilde{x}-x|| \leq \frac{5r}{4} . Also, ||\tilde{s}-s|| \leq 2d by triangle inequality.
Therefore, \begin{align}\begin{aligned} -\Re {[w - z(x,s)]}^2 & \leq - ||\tilde{x}-x||^2 + a^2 ||\tilde{x}-x||^2 + A^2 ||\tilde{s}-s||^2 + 2aA ||\tilde{x}-x|| \: ||\tilde{s}-s|| \\ & \leq \frac{-15}{16} ||\tilde{x}-x||^2 + A^2 ||\tilde{s}-s||^2 + \frac{A}{2} ||\tilde{x}-x|| \: ||\tilde{s}-s|| \\ & \leq \frac{-r^2}{64} . \end{aligned}\end{align}
In other words, \left| e^{-\ell[w-z(x,s)]^2}\right| \leq e^{-\ell r^2 / 64} , or \left| {\left(\frac{\ell}{\pi}\right)}^{n/2} \int_{(x,s)\in D} e^{-\ell [w - z(x,s)]^2} f(x,s) \, dg(x) \wedge dz(x,s) \right| \leq C \ell^{n/2} e^{-\ell r^2 / 64} , for some constant C. Note that D depends on y'. The set of all y' with ||y'|| \leq d, is a compact set, so we can make C large enough to not depend on the y' that was chosen. The claim follows.
For the given r>0 and d>0, \begin{align}\begin{aligned} \lim_{\ell\to\infty} {\left(\frac{\ell}{\pi}\right)}^{n/2} \int_{x \in \mathbb{R}^n} e^{ -\ell [\tilde{x}+i\varphi(\tilde{x},y') - x-i\varphi(x,y')]^2 } g(x) f(x,y') dx_1 \wedge \cdots \wedge dx_{n-1} \wedge \bigl(dx_{n} + i d_x \psi (x,y') \bigr) \\ = f(\tilde{x},y')\end{aligned}\end{align} uniformly in (\tilde{x},y') \in K'.
That is, we look at \eqref{eq:1} and we plug in w = z(\tilde{x},y') \in K. The g (as usual) makes sure we never evaluate f, \psi, or \varphi at points where they are not defined.
- Proof
-
The change of variables formula implies dx_1 \wedge \cdots \wedge dx_{n-1} \wedge \bigl(dx_{n} + i d_x \psi (x,y') \bigr) = d_x z(x,y') = \det \left[\frac{\partial z}{\partial x}(x,y')\right] dx , where \bigl[\frac{\partial z}{\partial x}(x,y')\bigr] is the matrix corresponding to the derivative of the mapping z with respect to the x variables evaluated at (x,y').
Let us change variables of integration via \xi = \sqrt{\ell} ( x-\tilde{x}): \begin{align}\begin{aligned} &{\left(\frac{\ell}{\pi}\right)}^{n/2} \int_{x \in \mathbb{R}^n} e^{ -\ell [\tilde{x}+i\varphi(\tilde{x},y') - x-i\varphi(x,y')]^2 } g(x) f(x,y') \det \left[\frac{\partial z}{\partial x}(x,y')\right] dx = \\ &{\left(\frac{1}{\pi}\right)}^{n/2} \int_{\xi \in \mathbb{R}^n} e^{-{\left[\xi + i\sqrt{\ell}\left(\varphi\left(\tilde{x}+\frac{\xi}{\sqrt{\ell}},y'\right) - \varphi(\tilde{x},y')\right)\right ]}^2} g\left(\tilde{x}+\frac{\xi}{\sqrt{\ell}}\right) f\left(\tilde{x}+\frac{\xi}{\sqrt{\ell}},y'\right) \det \left[\frac{\partial z}{\partial x}\left(\tilde{x}+\frac{\xi}{\sqrt{\ell}},y'\right)\right] d\xi .\end{aligned}\end{align} We now wish to take a limit as \ell \to \infty and for this we apply the dominated convergence theorem. So we need to dominate the integrand. The second half of the integrand is uniformly bounded independent of \ell as x \mapsto g(x) f(x,y') \det \left[\frac{\partial z}{\partial x}(x,y')\right] is a continuous function with compact support (because of g). Hence it is enough to worry about the exponential term. We also only consider those \xi where the integrand is not zero. Recall that r and d are small enough that
\sup_{||\hat{x}|| \leq r, ||\hat{y}'|| \leq d} \left| \left| \,\left[ \frac{ \partial \varphi}{\partial x}(\hat{x},\hat{y}') \right]\,\right| \right| \leq \frac{1}{4} , and as ||\tilde{x}|| \leq \frac{r}{4} (as (\tilde{x},y') \in K) and \left| \left| \tilde{x}+\frac{\xi}{\sqrt{\ell}}\right| \right| \leq r (because g is zero otherwise), then
\left| \left| \varphi\left(\tilde{x}+\frac{\xi}{\sqrt{\ell}},y'\right) - \varphi(\tilde{x},y')\right| \right| \leq \frac{1}{4} \left| \left| \tilde{x}+\frac{\xi}{\sqrt{\ell}}-\tilde{x}\right| \right| = \frac{|| \xi|| }{4 \sqrt{\ell}} .
So under the same conditions we have \begin{align}\begin{aligned} \left| e^{-{\left[\xi + i\sqrt{\ell}\left(\varphi\left(\tilde{x}+\frac{\xi}{\sqrt{\ell}},y'\right) - \varphi(\tilde{x},y')\right)\right]}^2}\right| & = e^{-\Re {\left[\xi + i\sqrt{\ell}\left(\varphi\left(\tilde{x}+\frac{\xi}{\sqrt{\ell}},y'\right) - \varphi(\tilde{x},y')\right)\right]}^2} \\ & = e^{-||\xi||^2 + \ell \left| \left| \varphi\left(\tilde{x}+\frac{\xi}{\sqrt{\ell}},y'\right) - \varphi(\tilde{x},y')\right| \right| ^2} \\ & \leq e^{-(15/16)|| \xi|| ^2} . \end{aligned}\end{align}
And that is integrable. Thus, take the pointwise limit under the integral to obtain {\left(\frac{1}{\pi}\right)}^{n/2} \int_{\xi \in \mathbb{R}^n} e^{-{\left[\xi + i\left[ \frac{\partial \varphi}{\partial x}(\tilde{x},y') \right] \xi \right]}^2} g(\tilde{x}) f(\tilde{x},y') \det \left[\frac{\partial z}{\partial x}(\tilde{x},y')\right] d\xi . In the exponent, we have an expression for the derivative in the \xi direction with y' fixed. If (\tilde{x},y') \in K', then g(\tilde{x}) = 1, and so we can ignore g.
Let A = I + i \bigl[ \frac{\partial \varphi}{\partial x}(\tilde{x},y') \bigr]. Lemma \PageIndex{1} says {\left(\frac{1}{\pi}\right)}^{n/2} \int_{\xi \in \mathbb{R}^n} e^{-{\left[\xi + i\left[ \frac{\partial \varphi}{\partial x}(\tilde{x},y') \right] \xi \right]}^2} f(\tilde{x},y') \det \left[\frac{\partial z}{\partial x}(\tilde{x},y')\right] d\xi = f(\tilde{x},y') .
That the convergence is uniform in (\tilde{x},y') \in K' is left as an exercise.
In the claim above, finish the proof that the convergence is uniform in (\tilde{x},y') \in K'. Hint: It may be easier to use the form of the integral before the change of variables and prove that the sequence is uniformly Cauchy.
We are essentially done with the proof of the theorem. The two claims together with \eqref{eq:1} show that f_\ell are entire holomorphic functions that approximate f uniformly on K. Entire holomorphic functions can be approximated by polynomials uniformly on compact subsets; simply take the partial sums of Taylor series at the origin.
Explain why being approximable on K by (holomorphic) polynomials does not necessarily mean that f is real-analytic.
Suppose M \subset \mathbb{C}^n is given by \Im z_n = 0. Use the standard Weierstrass approximation theorem to show that given a K \subset \subset M, and a smooth CR function f \colon M \to \mathbb{C}, then f can be uniformly approximated by holomorphic polynomials on K.


