3.2: CR Functions
- Page ID
- 74235
We first need to know what it means for a function \(f \colon X \to \mathbb{C}\) to be smooth if \(X\) is not an open set, for example, if \(X\) is a hypersurface.
Let \(X \subset \mathbb{R}^n\) be a set. The function \(f \colon X \to \mathbb{C}\) is smooth (resp. real-analytic) if for each point \(p \in X\) there is a neighborhood \(U \subset \mathbb{R}^n\) of \(p\) and a smooth (resp. real-analytic) \(F \colon U \to \mathbb{C}\) such that \(F(q) = f(q)\) for \(q \in X \cap U\).
For an arbitrary set \(X\), issues surrounding this definition can be rather subtle. The definition is easy to work with, however, if \(X\) is nice, such as a hypersurface, or if \(X\) is a closure of a domain with smooth boundary.
Suppose \(M \subset \mathbb{R}^n\) is a smooth (resp. real-analytic) real hypersurface. A function \(f \colon M \to \mathbb{C}\) is smooth (resp. real-analytic) if and only if whenever near any point we write \(M\) in coordinates \((x,y) \in \mathbb{R}^{n-1} \times \mathbb{R}\) as \[y = \varphi(x) , \] for a smooth (resp. real-analytic) function \(\varphi\), then the function \(f\bigl(x,\varphi(x)\bigr)\) is a smooth (resp. real-analytic) function of \(x\).
Prove the proposition.
Prove that if \(M\) is a smooth or real-analytic hypersurface, and \(f \colon M \to \mathbb{C}\) is smooth or real-analytic, then the function \(F\) from the definition is never unique, even for a fixed neighborhood \(U\).
Suppose \(M \subset \mathbb{R}^n\) is a smooth hypersurface, \(f \colon M \to \mathbb{C}\) is a smooth function, \(p \in M\), and \(X_p \in T_p M\). Prove that \(X_p f\) is well-defined. That is, suppose \(U\) is a neighborhood of \(p\), \(F \colon U \to \mathbb{C}\) and \(G \colon U \to \mathbb{C}\) are smooth functions that both equal \(f\) on \(U \cap M\). Prove that \(X_p F = X_p G\).
Due to the last exercise, we can apply vectors of \(T_p M\) to a smooth function on a hypersurface by simply applying them to any smooth extension. We can similarly apply vectors of \(\mathbb{C} \otimes T_p M\) to smooth functions on \(M\), as \(\mathbb{C} \otimes T_p M\) is simply the complex span of vectors in \(T_p M\).
Let \(M \subset \mathbb{C}^n\) be a smooth real hypersurface. A smooth \(f \colon M \to \mathbb{C}\) is a smooth CR function if \[X_p f = 0 \] for all \(p \in M\) and all vectors \(X_p \in T^{(0,1)}_p M\).
One only needs one derivative (rather than \(C^\infty\)) in the definition above. One can even define a continuous CR function if the derivative is taken in the distribution sense, but we digress.
When \(n=1\), a real hypersurface \(M \subset \mathbb{C}\) is a curve and \(T^{(0,1)}_p M\) is trivial. Therefore, all functions \(f \colon M \to \mathbb{C}\) are CR functions.
Let \(M \subset U\) be a smooth (resp. real-analytic) real hypersurface in an open \(U \subset \mathbb{C}^n\). Suppose \(F \colon U \to \mathbb{C}\) is a holomorphic function, then the restriction \(f = F|_M\) is a smooth (resp. real-analytic) CR function.
- Proof
-
First let us prove that \(f\) is smooth. The function \(F\) is smooth and defined on a neighborhood of any point, and so it can be used in the definition. Similarly for real-analytic.
Let us show \(f\) is CR at some \(p \in M\). Differentiating \(f\) with vectors in \(\mathbb{C} \otimes T_pM\) is the same as differentiating \(F\). As \(T_p^{(0,1)} M \subset T_p^{(0,1)} \mathbb{C}^n\), we have \[X_p f = X_p F = 0 \qquad \text{for all} \quad X_p \in T_p^{(0,1)} M. \]
On the other hand, not every smooth CR function is a restriction of a holomorphic function.
Take the smooth function \(f \colon \mathbb{R} \to \mathbb{R}\) we defined before that is not real-analytic at the origin. Take \(M \subset \mathbb{C}^2\) be the set defined by \(\Im z_2 = 0\). \(M\) is a real-analytic real hypersurface. Clearly \(T_p^{(0,1)} M\) is one-complex-dimensional, and at each \(p \in M\), \(\frac{\partial}{\partial \bar{z}_1}\big|_p\) is tangent and spans \(T_p^{(0,1)} M\). Define \(g \colon M \to \mathbb{C}\) by \[g(z_1,z_2,\bar{z}_1,\bar{z}_2) = f(\Re z_2) .\] Then \(g\) is CR as it is independent of \(\bar{z}_1\). If \(G \colon U \subset \mathbb{C}^2 \to \mathbb{C}\) is a holomorphic function where \(U\) is some open set containing the origin, then \(G\) restricted to \(M\) must be real-analytic (a power series in \(\Re z_1\), \(\Im z_1\), and \(\Re z_2\)) and therefore \(G\) cannot equal to \(g\) on \(M\).
Suppose \(M \subset \mathbb{C}^n\) is a smooth real hypersurface and \(f \colon M \to \mathbb{C}\) is a CR function that is a restriction of a holomorphic function \(F \colon U \to \mathbb{C}\) defined in some neighborhood \(U \subset \mathbb{C}^n\) of \(M\). Show that \(F\) is unique, that is if \(G \colon U \to \mathbb{C}\) is another holomorphic function such that \(G|_M = f = F|_M\), then \(G=F\).
Show that there is no maximum principle of CR functions. In fact, find a smooth real hypersurface \(M \subset \mathbb{C}^n\), \(n \geq 2\), and a smooth CR function \(f\) on \(M\) such that \(|f|\) attains a strict maximum at a point.
Suppose \(M \subset \mathbb{C}^n\), \(n \geq 2\), is the hypersurface given by \(\Im z_n = 0\). Show that every smooth CR function on \(M\) is holomorphic in the variables \(z_1,\ldots,z_{n-1}\). Use this to show that for no smooth CR function \(f\) on \(M\) can \(|f|\) attain a strict maximum on \(M\). But show that there do exist nonconstant functions such that \(|f|\) attains a (nonstrict) maximum \(M\).
Real-analytic CR functions on a real-analytic hypersurface \(M\) always extend to holomorphic functions of a neighborhood of \(M\). To prove this we wish to complexify everything, that is treat the \(z\)s and \(\bar{z}\)s as separate variables. The standard way of writing a hypersurface as a graph is not as convenient for this setting, so let us prove that for a real-analytic hypersurface, we can write it as a graph of a holomorphic function in the complexified variables. That is, using variables \((z,w)\), we will write \(M\) as a graph of \(\bar{w}\) over \(z\), \(\bar{z}\), and \(w\). This allows us to easily eliminate \(\bar{w}\) in any real-analytic expression.
Suppose \(M \subset \mathbb{C}^n\) is a real-analytic hypersurface and \(p \in M\). Then after a translation and rotation by a unitary matrix, \(p=0\), and near the origin in coordinates \((z,w) \in \mathbb{C}^{n-1} \times \mathbb{C}\), the hypersurface \(M\) is given by \[\bar{w} = \Phi(z,\bar{z},w) ,\] where \(\Phi(z,\zeta,w)\) is a holomorphic function defined on a neighborhood of the origin in \(\mathbb{C}^{n-1} \times \mathbb{C}^{n-1} \times \mathbb{C}\), such that \(\Phi\), \(\frac{\partial \Phi}{\partial z_j}\), \(\frac{\partial \Phi}{\partial \zeta_j}\) vanish at the origin for all \(j\), and \(w = \bar{\Phi}\bigl(\zeta,z,\Phi(z,\zeta,w)\bigr)\) for all \(z\), \(\zeta\), and \(w\).
A local basis for \(T^{(0,1)} M\) vector fields is given by \[\frac{\partial}{\partial \bar{z}_j} +\frac{\partial \Phi}{\partial \bar{z}_j} \frac{\partial}{\partial \bar{w}} \quad \left( = \frac{\partial}{\partial \bar{z}_j} +\frac{\partial \Phi}{\partial \zeta_j} \frac{\partial}{\partial \bar{w}} \right) , \qquad j=1,\ldots,n-1.\]
Finally, let \(\mathcal{M}\) be the set in \((z,\zeta,w,\omega) \in \mathbb{C}^{n-1} \times \mathbb{C}^{n-1} \times \mathbb{C} \times \mathbb{C}\) coordinates given near the origin by \(\omega = \Phi(z,\zeta,w)\). Then \(\mathcal{M}\) is the unique complexification of \(M\) near the origin in the sense that if \(f(z,\bar{z},w,\bar{w})\) is a real-analytic function vanishing on \(M\) near the origin, then \(f(z,\zeta,w,\omega)\) vanishes on \(\mathcal{M}\) near the origin.
- Proof
-
Translate and rotate so that \(M\) is given by \[\Im w = \varphi(z,\bar{z},\Re w) ,\] where \(\varphi\) is \(O(2)\). Write the defining function as \(r(z,\bar{z},w,\bar{w}) = -\frac{w-\bar{w}}{2i} +\varphi\bigl(z,\bar{z},\frac{w+\bar{w}}{2}\bigr)\). Complexifying, consider \(r(z,\zeta,w,\omega)\) as a holomorphic function of \(2n\) variables, and let \(\mathcal{M}\) be the set defined by \(r(z,\zeta,w,\omega) = 0\). The derivative of \(r\) in \(\omega\) (that is \(\bar{w}\)) does not vanish near the origin. Use the implicit function theorem for holomorphic functions to write \(\mathcal{M}\) near the origin as \[\omega = \Phi(z,\zeta,w) .\] Restrict to the diagonal, \(\bar{w} = \omega\) and \(\bar{z}=\zeta\), to get \(\bar{w} = \Phi(z,\bar{z},w)\). This is order 2 in the \(z\) and the \(\bar{z}\) since \(\varphi\) is \(O(2)\).
Because \(r\) is real-valued, then \(r(z,\bar{z},w,\bar{w}) = \overline{r(z,\bar{z},w,\bar{w})} = \bar{r}(\bar{z},z,\bar{w},w)\). Complexify to obtain \(r(z,\zeta,w,\omega) = \bar{r}(\zeta,z,\omega,w)\) for all \((z,\zeta,w,\omega)\) near the origin. If \(r(z,\zeta,w,\omega) = 0\), then \[0 = \overline{r(z,\zeta,w,\omega)} = \overline{\bar{r}(\zeta,z,\omega,w)} = r(\bar{\zeta},\bar{z},\bar{\omega},\bar{w}) =0.\] So, \((z,\zeta,w,\omega) \in \mathcal{M}\) if and only if \((\bar{\zeta},\bar{z},\bar{\omega},\bar{w}) \in \mathcal{M}\). Near the origin, \((z,\zeta,w,\omega) \in \mathcal{M}\) if and only if \(\omega = \Phi(z,\zeta,w)\), and hence if and only if \(\bar{w} = \Phi(\bar{\zeta},\bar{z},\bar{\omega})\). Conjugating, we get that \(\mathcal{M}\) is also given by \[w = \bar{\Phi}(\zeta,z,\omega).\] As \(\bigl(z,\zeta,w,\Phi(z,\zeta,w)\bigr) \in \mathcal{M}\), then for all \(z\), \(\zeta\), and \(w\), \[w = \bar{\Phi}\bigl(\zeta,z,\Phi(z,\zeta,w)\bigr).\]
The vector field \(X_j = \frac{\partial}{\partial \bar{z}_j} +\frac{\partial \Phi}{\partial \bar{z}_j} \frac{\partial}{\partial \omega}\) annihilates the function \(\Phi(z,\bar{z},w)-\bar{w}\), but that is not enough. The vector field must annihilate a real defining function such as the real part of \(\Phi(z,\bar{z},w)-\bar{w}\). So \(X_j\) must also annihilate the conjugate \(\bar{\Phi}(\bar{z},z,\bar{w})-w\), at least on \(M\). Compute, for \((z,w) \in M\),
\[\begin{align}\begin{aligned} X_j \bigl[\bar{\Phi}(\bar{z},z,\bar{w})-w\bigr] &= \frac{\partial \bar{\Phi}}{\partial \bar{z}_j} (\bar{z},z,\bar{w}) + \frac{\partial \Phi}{\partial \bar{z}_j} (z,\bar{z},w) \frac{\partial \bar{\Phi}}{\partial \bar{w}} (\bar{z},z,\bar{w}) \\ & = \frac{\partial \bar{\Phi}}{\partial \bar{z}_j} \bigl(\bar{z},z,\Phi(z,\bar{z},\bar{w})\bigr) + \frac{\partial \Phi}{\partial \bar{z}_j} (z,\bar{z},w) \frac{\partial \bar{\Phi}}{\partial \bar{w}} \bigl(\bar{z},z,\Phi(z,\bar{z},\bar{w})\bigr) \\ & = \frac{\partial}{\partial \bar{z}_j} \Bigl[ \bar{\Phi}\bigl(\bar{z},z,\Phi(z,\bar{z},w)\bigr) \Bigr] = \frac{\partial}{\partial \bar{z}_j} \Bigl[ w \Bigr] = 0 . \end{aligned}\end{align}\]
The last claim of the proposition is left as an exercise.
Again as a slight abuse of notation \(\Phi\) refers to both the function \(\Phi(z,\zeta,w)\) and \(\Phi(z,\bar{z},w)\).
Why do we say the last claim in the proposition proves the “uniqueness” of the complexification? Suppose we defined a complexification \(\mathcal{M}'\) by another holomorphic equation \(f=0\). By the claim, \(\mathcal{M} \subset \mathcal{M}'\), at least near the origin. If the derivative \(df\) is nonzero at the origin, then \(f\bigl(z,\zeta,w,\Phi(z,\zeta,w)\bigr) = 0\) implies that \(\frac{\partial f}{\partial \omega}\) is nonzero at the origin. Using the holomorphic implicit function theorem we can uniquely solve \(f=0\) for \(\omega\) near the origin, that unique solution is \(\Phi\), and hence \(\mathcal{M}' = \mathcal{M}\) near the origin.
As an example, recall that the sphere (minus a point) in \(\mathbb{C}^2\) is biholomorphic to the hypersurface given by \(\Im w = |z|^2\). That is, \(\frac{w-\bar{w}}{2i} = z \bar{z}\). Solving for \(\bar{w}\) and using \(\zeta\) and \(\omega\) obtains the equation for the complexification \(\omega = -2iz \zeta + w\). Then \(\Phi(z,\zeta,w) = -2iz \zeta + w\), and \(\bar{\Phi}(\zeta,z,\omega) = 2i\zeta z + \omega\). Let us check that \(\Phi\) is the right sort of function: \(\bar{\Phi}\bigl(z,\zeta,\Phi(z,\zeta,w)\bigr) = 2i\zeta z + (-2i z \zeta + w) = w\). The CR vector field is given by \(\frac{\partial}{\partial \bar{z}} +2i z \frac{\partial}{\partial \bar{w}}\).
Finish the proof of the proposition: Let \(M\subset \mathbb{C}^n\) be a real-analytic hypersurface given by \(\bar{w} = \Phi(z,\bar{z},w)\) near the origin, as in the proposition. Let \(f(z,\bar{z},w,\bar{w})\) be a real-analytic function such that \(f=0\) on \(M\). Prove that the complexified \(f(z,\zeta,w,\omega)\) vanishes on \(\mathcal{M}\).
In the proposition we only rotated and translated. Sometimes the following change of coordinates is also done. Prove that one can change coordinates (no longer linear) so that the \(\Phi\) in the proposition is such that \(\Phi(z,0,w) = \Phi(0,\zeta,w) = w\) for all \(z\), \(\zeta\), and \(w\). These coordinates are called normal coordinates.
Suppose \(\Phi\) is a holomorphic function defined on a neighborhood of the origin in \(\mathbb{C}^{n-1} \times \mathbb{C}^{n-1} \times \mathbb{C}\).
- Show that \(\bar{w} = \Phi(z,\bar{z},w)\) defines a real-analytic hypersurface near the origin if and only \(w = \bar{\Phi}\bigl(\zeta,z,\Phi(z,\zeta,w)\bigr)\) for all \(z\), \(\zeta\), and \(w\). Hint: One direction was proved already.
- As an example, show that \(\bar{w} = z\bar{z}\) does not satisfy the condition above, nor does it define a real hypersurface.
Let us prove that real-analytic CR functions on real-analytic hypersurfaces are restrictions of holomorphic functions. To motivate the proof, consider a real-analytic function \(f\) on the circle \(|z|^2 = z \bar{z} = 1\) (\(f\) is vacuously CR). This \(f\) is a restriction of a real-analytic function on a neighborhood of the circle, that we write \(f(z,\bar{z})\). On the circle \(\bar{z} = \frac{1}{z}\). Thus, \(F(z) = f\bigl(z,\frac{1}{z}\bigr)\) is a holomorphic function defined on a neighborhood of the circle and equal to \(f\) on the circle. Our strategy then is to solve for one of the barred variables via Proposition \(\PageIndex{3}\), and hope the CR conditions take care of the rest of the barred variables in more than one dimension.
Severi
Suppose \(M \subset \mathbb{C}^n\) is a real-analytic hypersurface and \(p \in M\). For every real-analytic CR function \(f \colon M \to \mathbb{C}\), there exists a holomorphic function \(F \in \mathcal{O}(U)\) for a neighborhood \(U\) of \(p\) such that \(F(q) = f(q)\) for all \(q \in M \cap U\).
- Proof
-
Write \(M\) near \(p\) as \(\bar{w} = \Phi(z,\bar{z},w)\). Let \(\mathcal{M}\) be the set in the \(2n\) variables \((z,w,\zeta,\omega)\) given by \(\omega = \Phi(z,\zeta,w)\). Take \(f\) and consider any real-analytic extension of \(f\) to a neighborhood of \(p\) and write it \(f(z,w,\bar{z},\bar{w})\). Complexify\(^{1}\) as before to \(f(z,w,\zeta,\omega)\). On \(\mathcal{M}\) we have \(f(z,w,\zeta,\omega) = f\bigl(z,w,\zeta,\Phi(z,\zeta,w)\bigr)\). Let \[F(z,w,\zeta) = f\bigl(z,w,\zeta,\Phi(z,\zeta,w)\bigr).\] Clearly \(F(z,w,\bar{z})\) equals \(f\) on \(M\). As \(f\) is a CR function, it is annihilated by \(\frac{\partial}{\partial \bar{z}_j} +\frac{\partial \Phi}{\partial \bar{z}_j} \frac{\partial}{\partial \bar{w}}\) on \(M\). So \[\frac{\partial F}{\partial \zeta_j} +\frac{\partial \Phi}{\partial \zeta_j} \frac{\partial F}{\partial \omega} = \frac{\partial F}{\partial \zeta_j} = 0\] on \(M \subset \mathcal{M}\). We have a real analytic function \(\frac{\partial F}{\partial \zeta_j}(z,w,\bar{z})\) that is zero on \(M\), so \(\frac{\partial F}{\partial \zeta_j}(z,w,\zeta) = 0\) on \(\mathcal{M}\) (Proposition \(\PageIndex{3}\) again). As \(\frac{\partial F}{\partial \zeta_j}\) is a function only of \(z\), \(w\), and \(\zeta\) (and not of \(\omega\)), \(\frac{\partial F}{\partial \zeta_j} = 0\) for all \((z,w,\zeta)\) in a neighborhood of the origin. Consequently, \(F\) does not depend on \(\zeta\), and \(F\) is actually a holomorphic function of \(z\) and \(w\) only and \(F = f\) on \(M\).
The most important place where we find CR functions that aren’t necessarily real-analytic is as boundary values of holomorphic functions.
Suppose \(U \subset \mathbb{C}^n\) is an open set with smooth boundary. Suppose \(f \colon \overline{U} \to \mathbb{C}\) is a smooth function, holomorphic on \(U\). Then \(f|_{\partial U}\) is a smooth CR function.
- Proof
-
The function \(f|_{\partial U}\) is clearly smooth.
Suppose \(p \in \partial U\). If \(X_p \in T_p^{(0,1)} \partial U\) is such that \[X_p = \sum_{j=1}^n a_j \frac{\partial}{\partial \bar{z}_j} \Big|_p ,\] take \(\{ q_k \}\) in \(U\) that approaches \(p\), then take \[X_{q_k} = \sum_{j=1}^n a_j \frac{\partial}{\partial \bar{z}_j} \Big|_{q_k} .\] Then \(X_{q_k} f = 0\) for all \(k\) and by continuity \(X_p f = 0\).
The boundary values of a holomorphic function define the function uniquely. That is, if two holomorphic functions continuous up to the (smooth) boundary are equal on an open set of the boundary, then they are equal in the domain:
Suppose \(U \subset \mathbb{C}^n\) is a domain with smooth boundary and \(f \colon \overline{U} \to \mathbb{C}\) is a continuous function, holomorphic on \(U\). If \(f=0\) on a nonempty open subset of \(\partial U\), then \(f=0\) on all of \(U\).
- Proof
-
Take \(p \in \partial U\) such that \(f=0\) on a neighborhood of \(p\) in \(\partial U\). Consider a small neighborhood \(\Delta\) of \(p\) such that \(f\) is zero on \(\partial U \cap \Delta\). Define \(g \colon \Delta \to \mathbb{C}\) by setting \(g(z) = f(z)\) if \(z \in U\) and \(g(z) = 0\) otherwise. See Figure \(\PageIndex{1}\). It is not hard to see that \(g\) is continuous, and it is clearly holomorphic where it is not zero. Radó’s theorem (Theorem 2.4.3) says that \(g\) is holomorphic, and as it is zero on a nonempty open subset of \(\Delta\), it is identically zero on \(\Delta\), meaning \(f\) is zero on a nonempty open subset of \(U\), and we are done by identity.
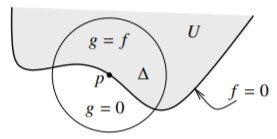
Figure \(\PageIndex{1}\)
Find a domain \(U \subset \mathbb{C}^n\), \(n \geq 2\), with smooth boundary and a smooth CR function \(f \colon \partial U \to \mathbb{C}\) such that there is no holomorphic function on \(U\) or \(\mathbb{C}^n \setminus U\) continuous up to the boundary and whose boundary values are \(f\).
- Suppose \(U \subset \mathbb{C}^n\) is a bounded open set with smooth boundary, \(f \colon \overline{U} \to \mathbb{C}\) is a continuous function, holomorphic in \(U\), and \(f|_{\partial U}\) is real-valued. Show that \(f\) is constant.
- Find a counterexample to the statement if you allow \(U\) to be unbounded.
Find a smooth CR function on the sphere \(S^{2n-1} \subset \mathbb{C}^n\) that is not a restriction of a holomorphic function of a neighborhood of \(S^{2n-1}\).
Show a global version of Severi. Given a real-analytic hypersurface \(M \subset \mathbb{C}^n\) and a real-analytic CR function \(f \colon M \to \mathbb{C}\), show that there exists a neighborhood \(U\) of \(M\), and an \(F \in \mathcal{O}(U)\) such that \(F|_U = f\).
A problem we tackle next is to try to extend a smooth CR function from the boundary of a domain to a holomorphic function inside. This is a PDE problem where the PDE are the Cauchy–Riemann equations, and the function on the boundary is the boundary condition. Cauchy–Riemann equations are overdetermined, that is, there are too many equations. Not every data on the boundary gives a solution. Proposition \(\PageIndex{4}\) says that the data being CR is a necessary condition for a solution (it is not sufficient in general). Proposition \(\PageIndex{5}\) says the solution is unique if it exists.
Footnotes
[1] At this point \(f\) stands for three distinct objects: the function on \(M\), its real-analytic extension to a neighborhood in \(\mathbb{C}^n\), and its complexification to a neighborhood of \((p,\bar{p})\) in \(\mathbb{C}^n \times \mathbb{C}^n\).


