3.1: Real-Analytic Functions and Complexification
- Page ID
- 74234
Let \(U \subset \mathbb{R}^n\) be open. A function \(f \colon U \to \mathbb{C}\) is real-analytic (or simply analytic if clear from context) if at each point \(p \in U\), the function \(f\) has a convergent power series that converges (absolutely) to \(f\) in some neighborhood of \(p\). A common notation for real-analytic is \(C^\omega\).
Before we discuss the connection to holomorphic functions, we prove a simple lemma.
Let \(\mathbb{R}^n \subset \mathbb{C}^n\) be the natural inclusion and \(V \subset \mathbb{C}^n\) a domain such that \(V \cap \mathbb{R}^n \not= \emptyset\). Suppose \(f,g \colon V \to \mathbb{C}\) are holomorphic functions such that \(f=g\) on \(V \cap \mathbb{R}^n\). Then \(f=g\) on \(V\).
- Proof
-
Considering \(f-g\) we may assume that \(g=0\). Let \(z = x+iy\) as usual so that \(\mathbb{R}^n\) is given by \(y=0\). Our assumption is that \(f = 0\) when \(y=0\), so the derivative of \(f\) with respect to \(x_j\) is zero. When \(y=0\), the Cauchy–Riemann equations say \[0 = \frac{\partial f}{\partial x_j} = -i \frac{\partial f}{\partial y_j} .\] Therefore, on \(y=0\), \[\frac{\partial f }{\partial z_j} = 0 .\] The derivative \(\frac{\partial f }{\partial z_j}\) is holomorphic and \(\frac{\partial f }{\partial z_j} = 0\) on \(y=0\). By induction all holomorphic derivatives of \(f\) at \(p \in \mathbb{R}^n \cap V\) vanish, and \(f\) has a zero power series. Hence \(f\) is identically zero in a neighborhood of \(p\) in \(\mathbb{C}^n\) and by the identity theorem it is zero on all of \(V\).
We return to \(\mathbb{R}^n\) for a moment. We write a power series in \(\mathbb{R}^n\) in multinomial notation as usual. Suppose that for some \(a \in \mathbb{R}^n\) and some polyradius \(r=(r_1,\ldots,r_n)\), the series \[\sum_{\alpha} c_{\alpha} {(x-a)}^\alpha\] converges whenever \(|x_j-a_j| \leq r_j\) for all \(j\). Here convergence is absolute convergence. That is, \[\sum_{\alpha} |c_{\alpha}| \, |x-a|^\alpha\] converges. If we replace \(x_j \in \mathbb{R}\) with \(z_j \in \mathbb{C}\) such that \(|z_j-a_j| \leq |x_j-a_j|\), then the series still converges. Hence the series \[\sum_{\alpha} c_{\alpha} {(z-a)}^\alpha\] converges absolutely in \(\Delta_r(a) \subset \mathbb{C}^n\).
Suppose \(U \subset \mathbb{R}^n\) is a domain and \(f \colon U \to \mathbb{C}\) is real-analytic. Let \(\mathbb{R}^n \subset \mathbb{C}^n\) be the natural inclusion. Then there exists a domain \(V \subset \mathbb{C}^n\) such that \(U \subset V\) and a unique holomorphic function \(F \colon V \to \mathbb{C}\) such that \(F|_U = f\).
- Proof
-
We proved the local version already. But we must prove that if we extend our \(f\) near every point, we always get the same function. That follows from Lemma \(\PageIndex{1}\); any two such functions are equal on \(\mathbb{R}^n\), and hence equal. There is a subtle topological technical point in this, so let us elaborate. A key topological fact is that we define \(V\) as a union of the polydiscs where the series converges. If a point \(p\) is in two different such polydiscs, we need to show that the two definitions of \(F\) are the same at \(p\). But the intersection of two polydiscs is always connected, and in this case contains a piece of \(\mathbb{R}^n\) as well, and we may apply the lemma above.
Among many other things that follow from this proposition, we can now conclude that a real-analytic function is \(C^\infty\) smooth. Be careful and notice that \(U\) is a domain in \(\mathbb{R}^n\), but it is not an open set when considered as a subset of \(\mathbb{C}^n\). Furthermore, \(V\) may be a very “thin” neighborhood around \(U\). There is no way of finding \(V\) just from knowing \(U\). You need to also know \(f\). As an example, consider \(f(x) = \frac{1}{\epsilon^2+x^2}\) for \(\epsilon > 0\), which is real-analytic on \(\mathbb{R}\), but the complexification is not holomorphic at \(\pm \epsilon i\).
Prove the identity theorem for real-analytic functions. That is, if \(U \subset \mathbb{R}^n\) is a domain, \(f \colon U \to \mathbb{R}\) a real-analytic function and \(f\) is zero on a nonempty open subset of \(U\), then \(f\) is identically zero.
Suppose \(U \subset \mathbb{R}^n\) is a domain and \(f \colon U \to \mathbb{R}\) a real-analytic function. Suppose that \(W \subset U\) is a nonempty open subset and \(f|_W\) is harmonic. Prove that \(f\) is harmonic.
Let \((0,1) \subset \mathbb{R}\). Construct a real-analytic function on \((0,1)\) that does not complexify to the rectangle \((0,1) + i(-\epsilon,\epsilon) \subset \mathbb{C}\) for any \(\epsilon > 0\). Why does this not contradict the proposition?
A polynomial \(P(x)\) in \(n\) real variables \((x_1,\ldots,x_n)\) is homogeneous of degree \(d\) if \(P(s x) = s^d P(x)\) for all \(s \in \mathbb{R}\) and \(x \in \mathbb{R}^n\). A homogeneous polynomial of degree \(d\) is a polynomial whose every monomial is of total degree \(d\). If \(f\) is real-analytic near \(a \in \mathbb{R}^n\), then write the power series of \(f\) at \(a\) as \[\sum_{j=0}^{\infty} f_j(x-a) ,\] where \(f_j\) is a homogeneous polynomial of degree \(j\). The \(f_j\) is called the degree \(j\) homogeneous part of \(f\) at \(a\).
There is usually a better way to complexify real-analytic functions in \(\mathbb{C}^n\). Suppose \(U \subset \mathbb{C}^n \cong \mathbb{R}^{2n}\), and \(f \colon U \to \mathbb{C}\) is real-analytic. Assume \(a=0 \in U\) for simplicity. Writing \(z = x+iy\), near \(0\), \[f(x,y) = \sum_{j=0}^\infty f_j(x,y) = \sum_{j=0}^\infty f_j\left( \frac{z+\bar{z}}{2}, \frac{z-\bar{z}}{2i}\right) .\] The polynomial \(f_j\) becomes a homogeneous polynomial of degree \(j\) in the variables \(z\) and \(\bar{z}\). The series becomes a power series in \(z\) and \(\bar{z}\). As mentioned before, we simply write the function as \(f(z,\bar{z})\), and we consider the power series representation in \(z\) and \(\bar{z}\) rather than in \(x\) and \(y\). In multinomial notation, we write a power series at \(a \in \mathbb{C}^n\) as \[\sum_{\alpha,\beta} c_{\alpha,\beta} {(z-a)}^\alpha {(\bar{z}-\bar{a})}^\beta .\]
A holomorphic function is real-analytic, but not vice versa. A holomorphic function is a real-analytic function that does not depend on \(\bar{z}\).
Before we discuss complexification in terms of \(z\) and \(\bar{z}\), we need the following lemma.
Let \(V \subset \mathbb{C}^n \times \mathbb{C}^n\) be a domain, let the coordinates be \((z,\zeta) \in \mathbb{C}^n \times \mathbb{C}^n\), let \[D = \bigl\{ (z,\zeta) \in \mathbb{C}^n \times \mathbb{C}^n : \zeta = \bar{z} \bigr\},\] and suppose \(D \cap V \not= \emptyset\). Suppose \(f,g \colon V \to \mathbb{C}\) are holomorphic functions such that \(f=g\) on \(D \cap V\). Then \(f=g\) on all of \(V\).
The set \(D\) is sometimes called the diagonal.
- Proof
-
Again assume without loss of generality that \(g=0\). Whenever \((z,\bar{z}) \in V\), we have \(f(z,\bar{z}) = 0\), which is really \(f\) composed with the map that takes \(z\) to \((z,\bar{z})\). As this composition is identically zero, applying the Wirtinger operators yields zero. Using the chain rule, \[0 = \frac{\partial}{\partial \bar{z}_j} \Bigl[f(z,\bar{z})\Bigr] = \frac{\partial f}{\partial \zeta_j}(z,\bar{z}) .\] Let us do this again with the \(z_j\), \[0 = \frac{\partial}{\partial z_j} \Bigl[f(z,\bar{z})\Bigr] = \frac{\partial f}{\partial z_j}(z,\bar{z}) .\] Either way, we get another holomorphic function in \(z\) and \(\zeta\) that is zero on \(D\). By induction, for all \(\alpha\) and \(\beta\) we get \[0 = \frac{\partial^{|\alpha|+|\beta|}}{\partial z^\alpha \partial \bar{z}^\beta} \Bigl[f(z,\bar{z})\Bigr] = \frac{\partial^{|\alpha|+|\beta|} f}{\partial z^\alpha \partial \zeta^\beta}(z,\bar{z}) .\] All holomorphic derivatives in \(z\) and \(\zeta\) of \(f\) are zero on every point \((z,\bar{z})\), so the power series is zero at every point \((z,\bar{z})\), and so \(f\) is identically zero in a neighborhood of any point \((z,\bar{z})\). The lemma follows by the identity theorem.
Let \(f\) be a real-analytic function. Suppose the series (in multinomial notation) \[f(z,\bar{z}) = \sum_{\alpha,\beta} c_{\alpha,\beta} {(z-a)}^\alpha {(\bar{z}-\bar{a})}^\beta\] converges in a polydisc \(\Delta_r(a) \subset \mathbb{C}^n\). By convergence we mean absolute convergence, \[\sum_{\alpha,\beta}|c_{\alpha,\beta}| \, |z-a|^\alpha |\bar{z}-\bar{a}|^\beta\] converges. The series still converges if we replace \(\bar{z}_j\) with \(\zeta_j\) where \(|\zeta_j-\bar{a}| \leq |\bar{z}_j-\bar{a}|\). So the series \[F(z,\zeta) = \sum_{\alpha,\beta} c_{\alpha,\beta} {(z-a)}^\alpha {(\zeta-\bar{a})}^\beta\] converges (absolutely) for all \((z,\zeta) \in \Delta_r(a) \times \Delta_r(\bar{a})\).
Putting together the discussion above with the lemma we obtain:
Complexification Part II
Suppose \(U \subset \mathbb{C}^n\) is a domain and \(f \colon U \to \mathbb{C}\) is real-analytic. Then there exists a domain \(V \subset \mathbb{C}^n \times \mathbb{C}^n\) such that \[\bigl\{ (z,\zeta) : \zeta = \bar{z} \text{ and } z \in U \bigr\} \subset V ,\] and a unique holomorphic function \(F \colon V \to \mathbb{C}\) such that \(F(z,\bar{z}) = f(z,\bar{z})\) for all \(z \in U\).
The function \(f\) can be thought of as the restriction of \(F\) to the set where \(\zeta = \bar{z}\). We will abuse notation and write simply \(f(z,\zeta)\) both for \(f\) and its extension. The reason for this abuse is evident from the computations above. What we are calling \(f\) is a function of \((z,\bar{z})\) if thinking of it as a function on the diagonal where \(\zeta=\bar{z}\), or it is a function of \(z\) if thinking of it as just the function \(z \mapsto f(z,\bar{z})\), or it is the function \((z,\zeta) \mapsto f(z,\zeta)\). We have the following commutative diagram:
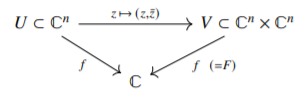
Figure \(\PageIndex{1}\)
All three ways of going from one place to another in the diagram we are calling \(f\). The arrow from \(V\) was called \(F\) in the proposition. The notation plays well with differentiation and the Wirtinger operators. Differentiating \(f\) (really the \(F\) in the proposition) in \(\zeta_j\) and evaluating at \((z,\bar{z})\) is the same thing as evaluating at \((z,\bar{z})\) and then differentiating in \(\bar{z}_j\) using the Wirtinger operator: \[\frac{\partial F}{\partial \zeta_j}(z,\bar{z}) = \frac{\partial f}{\partial \zeta_j}(z,\bar{z}) = \frac{\partial}{\partial \bar{z}_j}\Bigl[ f(z,\bar{z}) \Bigr] = \frac{\partial f}{\partial \bar{z}_j}(z,\bar{z}) .\] If we squint our mind’s eye, we can’t quite see the difference between \(\bar{z}\) and \(\zeta\). We have already used this idea for smooth functions, but for real-analytic functions we can treat \(z\) and \(\bar{z}\) as truly independent variables. The abuse of notation is entirely justified, at least once it is understood well.
The domain \(V\) in the proposition is not simply \(U\) times the conjugate of \(U\). In general, it is much smaller. For example, a real-analytic \(f \colon \mathbb{C}^n \to \mathbb{C}\) does not necessarily complexify to all of \(\mathbb{C}^n \times \mathbb{C}^n\). That is because the domain of convergence for a real-analytic function on \(\mathbb{C}^n\) is not necessarily all of \(\mathbb{C}^n\). In one dimension, \[f(z,\bar{z}) = \frac{1}{1+|z|^2}\] is real-analytic on \(\mathbb{C}\), but it is not a restriction to the diagonal of a holomorphic function on all of \(\mathbb{C}^2\). The problem is that the complexified function \[f(z,\zeta) = \frac{1}{1+z \zeta}\] is undefined on the set where \(z \zeta = -1\), which by a fluke never happens when \(\zeta = \bar{z}\).
This form of complexification is sometimes called polarization due to its relation to the polarization identities\(^{1}\): We can recover a Hermitian matrix \(A\), and therefore the sesquilinear form \(\langle Az, w\rangle \) for \(z,w\in \mathbb{C}^n\), by simply knowing the value of \[\langle Az, z\rangle = z^*Az = \sum_{j,k=1}^n a_{jk} \, \bar{z}_j z_k\] for all \(z \in \mathbb{C}^n\). In fact, under the hood Proposition \(\PageIndex{2}\) is polarization in an infinite-dimensional Hilbert space, but we digress.
Treating \(\bar{z}\) as a separate variable is a very powerful idea, and as we have just seen it is completely natural for real-analytic functions. This is one of the reasons why real-analytic functions play a special role in several complex variables.
Let \(U \subset \mathbb{C}^n\) be an open set and \(\varphi \colon U \to \mathbb{R}\) a pluriharmonic function. Prove that \(\varphi\) is real-analytic.
Let \(U \subset \mathbb{C}^n\) be an open set, \(z_0 \in U\). Suppose \(\varphi \colon U \to \mathbb{R}\) is a pluriharmonic function. You know that \(\varphi\) is real-analytic. Using complexification, write down a formula for a holomorphic function near \(z_0\) whose real part is \(\varphi\).
Let \(U \subset \mathbb{C}^n\) be a domain, and suppose \(f, g \in \mathcal{O}(U)\). Suppose that \(f = \bar{g}\) on \(U\). Use complexification (complexify \(f-\bar{g}\)) to show that both \(f\) and \(g\) are constant.
Not every \(C^\infty\) smooth function is real-analytic. For \(x \in \mathbb{R}\), define \[f(x) = \begin{cases} e^{-1/x^2} & \text{if $x > 0$,} \\ 0 & \text{if $x \leq 0$.} \end{cases}\] The function \(f \colon \mathbb{R} \to \mathbb{R}\) is \(C^\infty\) and \(f^{(k)}(0) = 0\) for all \(k\). The Taylor series of \(f\) at the origin does not converge to \(f\) in any neighborhood of the origin; it converges to the zero function but not to \(f\). Because of this, there is no neighborhood \(V\) of the origin in \(\mathbb{C}\) such that \(f\) is the restriction to \(V \cap \mathbb{R}\) of a holomorphic function in \(V\).
Prove the statements of the example above.
A real hypersurface \(M \subset \mathbb{R}^n\) is said to be real-analytic if locally at every point it is the graph of a real-analytic function. That is near every point (locally), after perhaps relabeling coordinates \(M\) can be written as a graph \[y = \varphi(x) , \] where \(\varphi\) is real-analytic, \((x,y) \in \mathbb{R}^{n-1} \times \mathbb{R} = \mathbb{R}^n\).
Compare this definition to the definition of Hypersurface. We could define a real-analytic hypersurface as in the definition for Hypersurface and then prove an analogue of Lemma 2.2.1 to show that this would be identical to the definition above. The definition we gave is sufficient, and so we avoid the complication and leave it to the interested reader.
Show that the definition above is equivalent to an analogue of the definition of Hypersurface. That is, state the alternative definition of real-analytic hypersurface and then prove the analogue of Lemma 2.2.1.
A mapping to \(\mathbb{R}^m\) is real-analytic if all the components are real-analytic functions. Via complexification we give a simple proof of the following result.
Let \(U \subset \mathbb{R}^n\), \(V \subset \mathbb{R}^k\) be open and let \(f \colon U \to V\) and \(g \colon V \to \mathbb{R}^m\) be real-analytic. Then \(g \circ f\) is real-analytic.
- Proof
-
Let \(x \in \mathbb{R}^n\) be our coordinates in \(U\) and \(y \in \mathbb{R}^k\) be our coordinates in \(V\). Complexify \(f(x)\) and \(g(y)\) by allowing \(x\) to be a complex vector in a small neighborhood of \(U\) in \(\mathbb{C}^n\) and \(y\) to be a complex vector in a small neighborhood of \(V\) in \(\mathbb{C}^k\). So treat \(f\) and \(g\) as holomorphic functions. On a certain neighborhood of \(U\) in \(\mathbb{C}^n\), the composition \(f \circ g\) makes sense and it is holomorphic, as composition of holomorphic mappings is holomorphic. Restricting the complexified \(f \circ g\) back to \(\mathbb{R}^n\) we obtain a real-analytic function.
The proof demonstrates a simple application of complexification. Many properties of holomorphic functions are easy to prove because holomorphic functions are solutions to certain PDE (the Cauchy–Riemann equations). There is no PDE that defines real-analytic functions, so complexification provides a useful tool to transfer certain properties of holomorphic functions to real-analytic functions. We must be careful, however. Hypotheses on real-analytic functions only give us hypotheses on certain points of the complexified holomorphic functions.
Demonstrate the point about complexification we made just above. Find a nonconstant bounded real-analytic \(f \colon \mathbb{R}^n \to \mathbb{R}\) that happens to complexify to \(\mathbb{C}^n\).
Let \(U \subset \mathbb{R}^n\) be open. Let \(\varphi \colon (0,1) \to U\) be a real-analytic function (curve), and let \(f \colon U \to \mathbb{R}\) be real-analytic. Suppose that \((f \circ \varphi)(t) = 0\) for all \(t \in (0,\epsilon)\) for some \(\epsilon > 0\). Prove that \(f\) is zero on the image \(\varphi\bigl((0,1)\bigr)\).
Footnotes
[1] Such as \(4 \langle z, w\rangle = ||z+w||^2-||z-w||^2 +i \bigl( ||z+iw||^2 - ||z-iw||^2 \bigr)\).


