6.2: Weierstrass Preparation and Division Theorems
( \newcommand{\kernel}{\mathrm{null}\,}\)
Suppose f is (a germ of) a holomorphic function at a point p∈Cn. Write f(z)=∞∑k=0fk(z−p), where fk is a homogeneous polynomial of degree k, that is, fk(tz)=tkfk(z).
Let p∈Cn and f be a function holomorphic in a neighborhood of p. If f is not identically zero, define ordpfdef=min{k∈N0:fk≢0}. If f≡0, then define ordpf=∞. The number ordpf is called the order of vanishing of f at p.
In other words, the order of vanishing of f at p is k, whenever all partial derivatives of order less than k vanish at p, and there exists at least one derivative of order k that does not vanish at p.
In one complex variable, a holomorphic function f with ord0f=k can be written (locally) as f(z)=zku(z) for a nonvanishing u. In several variables, there is a similar theorem, or in fact a pair of theorems, the so-called Weierstrass preparation and division theorems.
Let U⊂Cn−1 be open, and let z′∈Cn−1 denote the coordinates. Suppose a polynomial P∈O(U)[zn] is monic of degree k≥0, that is, P(z′,zn)=zkn+k−1∑j=0cj(z′)zjn, where cj are holomorphic functions defined on U, such that cj(0)=0 for all j. Then P is called a Weierstrauss polynomial of degree k. If the cj are germs in O0=n−1O0, then P∈O0[zn] and P is a germ of a Weierstrauss polynomial.
The definition (and the theorem that follows) still holds for n=1. If you read the definition carefully, you will find that if n=1, then the only Weierstrass polynomial of degree k is zk. Note that for any n, if k=0, then P=1.
The purpose of this section is to show that every holomorphic function in O0 is up to a unit and a possible small rotation a Weierstrass polynomial, which carries the zeros of f. Consequently the algebraic and geometric properties of nO0 can be understood via algebraic and geometric properties of n−1O0[zn].
Suppose f∈O(U) for an open U⊂Cn−1×C, where 0∈U, and f(0)=0. Suppose zn↦f(0,zn) is not identically zero near the origin and its order of vanishing at the origin is k≥1.
Then there exists an open polydisc V=V′×D⊂Cn−1×C with 0∈V⊂U, a unique u∈O(V), u(z)≠0 for all z∈V, and a unique Weierstrass polynomial P of degree k with coefficients holomorphic in V′ such that f(z′,zn)=u(z′,zn)P(z′,zn), and such that all k zeros (counting multiplicity) of zn↦P(z′,zn) lie in D for all z′∈V′
- Proof
-
There exists a small disc D⊂C centered at zero such that {0}ׯD⊂U and such that f(0,zn)≠0 for zn∈¯D∖{0}. By continuity of f, there is a small polydisc V=V′×D such that ¯V⊂U and f is not zero on V′×∂D. We will consider the zeros of zn↦f(z′,zn) for z′ near zero. See Figure 6.2.1.
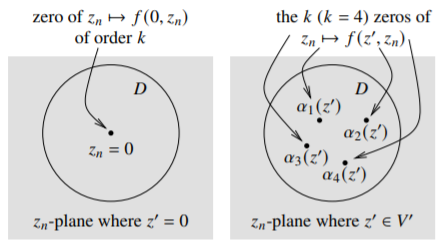
Figure 6.2.1
By the one-variable argument principle (Theorem B.25) the number of zeros (with multiplicity) of zn↦f(z′,zn) in D is 12πi∫∂D∂f∂zn(z′,ζ)f(z′,ζ) dζ. As f(z′,ζ) does not vanish when z′∈V′ and ζ∈∂D, the expression above is a continuous integer-valued function of z′∈V′. The expression is equal to k when z′=0, and so it is equal to k for all z′∈V′. Write the zeros of zn↦f(z′,zn) as α1(z′),…,αk(z′), including multiplicity. The zeros are not ordered in any particular way. Pick some ordering for every z′. Write P(z′,zn)=k∏j=1(zn−αj(z′))=zkn+ck−1(z′)zk−1n+⋯+c0(z′). For a fixed z′, P is uniquely defined as the ordering of zeros does not matter in its definition (see exercise below). It is clear that u and P are unique if they exist (that is, if they exist as holomorphic functions).
The functions αj are not even continuous in general (see Example 6.2.1). However, we will prove that the functions cj are holomorphic. The functions cj are (up to sign) the elementary symmetric functions of α1,…,αk (see below). It is a standard theorem in algebra (see Exercise 6.2.1) that the elementary symmetric functions are polynomials in the so-called power sum functions in the αjs: sm(z′)=k∑j=1αj(z′)m,m=1,…,k. Therefore, if we show that the power sums sm are holomorphic, then cℓ are holomorphic.
A refinement of the argument principle (see also Theorem B.25) says: If h and g are holomorphic functions on a disc D, continuous on ¯D, such that g has no zeros on ∂D, and α1,…,αk are the zeros of g in D, then 12πi∫∂Dh(ζ)g′(ζ)g(ζ) dζ=k∑j=1h(αj).
The formula above with h(ζ)=ζm and g(ζ)=f(z′,ζ) says that sm(z′)=k∑j=1αj(z′)m=12πi∫∂Dζm∂f∂ζ(z′,ζ)f(z′,ζ) dζ. The function sm is clearly continuous, and if we differentiate under the integral with ∂∂ˉzℓ for ℓ=1,…,n−1, we find that sm is holomorphic.
Finally, we wish to show that P divides f as claimed. For each fixed z′, one variable theory says that zn↦f(z′,zn)P(z′,zn) has only removable singularities, and in fact, it has no zeros as we defined P to exactly cancel them all out. The Cauchy formula on fP then says that the function u(z′,zn)=12πi∫∂Df(z′,ζ)P(z′,ζ)(ζ−zn)dζ is equal to f(z′,zn)P(z′,zn). The function u is clearly continuous and holomorphic in zn for each fixed z′. By differentiating under the integral, we find that it is also holomorphic in z′.
A useful example to keep in mind is f(z1,z2)=z22−z1, a Weierstrass polynomial in z2 of degree k=2. So z′=z1. For all z1 except the origin there are two zeros, ±√z1. Call one of them α1(z1) and one of them α2(z1). Recall there is no continuous choice of a square root that works for all z1, so no matter how you choose, α1 and α2 will not be continuous. At the origin there is only one zero of order two, so α1(0)=α2(0)=0. On the other hand the symmetric functions c1(z1)=−α1(z1)−α2(z1)=0 and c0(z′1)=α1(z1)α2(z1)=−z1 are holomorphic.
The k depends on the coordinates chosen. If we do a linear change of coordinates and consider g(z1,z2)=−f(z2,z1), then g(z1,z2)=z21−z2, which is a Weierstrass polynomial in z2 of degree k=1. After the change, there is only one zero, α1(z1)=z21, and so c0(z1)=−z21.
A function f(z1,…,zn) is symmetric if f=f∘p for all permutations of the variables p. The elementary symmetric functions of α1,…,αk are the coefficients σj of the polynomial k∏j=1(t+αj)=tk+σ1tk−1+⋯+σk−2t2+σk−1t+σk. In other words: σ1=α1+α2+⋯+αk,σ2=α1α2+α1α3+⋯+αk−1αk,⋮σk−1=α2α3⋯αk+α1α3α4⋯αk+⋯+α1α2⋯αk−1,σk=α1α2⋯αk. So for example when k=2, then σ2=α1α2 and σ1=α1+α2. The function σ1 happens to already be a power sum. We can write σ2 as a polynomial in the power sums: σ2=12((α1+α2)2−(α21+α22)).
Show that elementary symmetric functions are polynomials in the power sums.
Prove the fundamental theorem of symmetric polynomials: Every symmetric polynomial can be written as a polynomial in the elementary symmetric functions. Use the following procedure. Using double induction, suppose the theorem is true if the number of variables is less than k, and the theorem is true in k variables for degree less than d. Consider a symmetric P(z1,…,zk) of degree d. Write P(z1,…,zk−1,0) by induction hypothesis as a polynomial in the elementary symmetric functions of one less variable. Use the same coefficients, but plug in the elementary symmetric functions of k variables except the symmetric polynomial in k variables of degree k, that is except the z1⋯zk. You will obtain a symmetric function L(z1,…,zk) and you need to show L(z1,…,zk−1,0)=P(z1,…,zk−1,0). Now use symmetry to prove that P(z1,…,zk)=L(z1,…,zk)+z1⋯zkQ(z1,…,zk). Then note that Q has lower degree and finish by induction.
Extend the previous exercise to power series. Suppose f(z1,…,zk) is a convergent symmetric power series at 0, show that f can be written as a convergent power series in the elementary symmetric functions.
Suppose P(z′,zn) is a Weierstrass polynomial of degree k, and write the zeros as α1(z′),…,αk(z′). These are not holomorphic functions, but suppose that f is a symmetric convergent power series at the origin in k variables. Show that f(α1(z′),…,αk(z′)) is a holomorphic function of z′ near the origin.
The hypotheses of the preparation theorem are not an obstacle. If a holomorphic function f is such that zn↦f(0,zn) vanishes identically, then we can make a small linear change of coordinates L (L can be a matrix arbitrarily close to the identity) such that f∘L satisfies the hypotheses of the theorem. For example, f(z1,z2,z3)=z1z3+z2z3 does not satisfy the hypotheses of the theorem as f(0,0,z3)≡0. But for an arbitrarily small ϵ≠0, replacing z2 with z2+ϵz3 leads to ˜f(z1,z2,z3)=f(z1,z2+ϵz3,z3)=z1z3+z2z3+ϵz23, and ˜f(0,0,z3)=ϵz23. Thence ˜f satisfies the hypotheses of the theorem.
Prove the fact above about the existence of L arbitrarily close to the identity.
Prove that a monic polynomial P(ζ) of one variable is uniquely determined by its zeros up to multiplicity. That is, suppose P and Q are two monic polynomials with the same zeros up to multiplicity, then P=Q. That proves the uniqueness of the Weierstrass polynomial.
Suppose D⊂C is a bounded domain, 0∈D, U′⊂Cn−1 is a domain, 0∈U′, and P∈O(U′)[zn] is a Weierstrass polynomial such that P(z′,zn) is not zero on U′×∂D. Then for any z′∈U, all zeros of zn↦P(z′,zn) are in D.
Let D⊂C be a bounded domain, and U′⊂Cn−1 a domain. Suppose f is a continuous function on U′ׯD holomorphic on U′×D, where f is zero on at least one point of U′×D, and f is never zero on U′×∂D. Prove that zn↦f(z′,zn) has at least one zero in D for every z′∈U′.
The order of vanishing of f at the origin is a lower bound on the number k in the theorem. The order of vanishing for a certain variable may be larger than this lower bound. If f(z1,z2)=z21+z32, then the k we get is 3, but ord0f=2. We can make a small linear change of coordinates to ensure k=ord0f. With the f as above, f(z1+ϵz2,z2) gives k=2 as expected.
The Weierstrass preparation theorem is a generalization of the implicit function theorem. When k=1 in the theorem, then we obtain the Weierstrass polynomial zn+c0(z′). That is, the zero set of f is a graph of the holomorphic function −c0. Therefore, the Weierstrass theorem is a generalization of the implicit function theorem to the case when ∂f∂zn is zero. We can still “solve” for zn, but we find k solutions given as the zeros of the obtained Weierstrass polynomial.
There is an obvious statement of the preparation theorem for germs.
State and prove a germ version of the preparation theorem.
Weierstrass Division Theorem
Suppose f is holomorphic near the origin, and suppose P is a Weierstrass polynomial of degree k≥1 in zn. Then there exists a neighborhood V of the origin and unique q,r∈O(V), where r is a polynomial in zn of degree less than k, and on V, f=qP+r.
Note that r need not be a Weierstrass polynomial; it need not be monic nor do the coefficients need to vanish at the origin. It is simply a polynomial in zn with coefficients that are holomorphic functions of the first n−1 variables.
- Proof
-
Uniqueness is left as an exercise. Consider a connected neighborhood V=V′×D of the origin, where D is a disc, f and P are continuous in V′ׯD, and P is not zero on V′×∂D. Let q(z′,zn)=12πi∫∂Df(z′,ζ)P(z′,ζ)(ζ−zn) dζ. As P is not zero on V′×∂D, the function q is holomorphic in V (differentiate under the integral). If P did divide f, then q would really be fP. But if P does not divide f, then the Cauchy integral formula does not apply and q is not equal to fP. Interestingly the expression does give the quotient in the division with remainder.
Write f using the Cauchy integral formula in zn and subtract qP to obtain r: r(z′,zn)=f(z′,zn)−q(z′,zn)P(z′,zn)=12πi∫∂Df(z′,ζ)P(z′,ζ)−f(z′,ζ)P(z′,zn)P(z′,ζ)(ζ−zn) dζ. We need to show r is a polynomial in zn of degree less than k. In the expression inside the integral, the numerator is of the form ∑jhj(z′,ζ)(ζj−zjn) and is therefore divisible by (ζ−zn). The numerator is a polynomial of degree k in zn. After dividing by (ζ−zn), the integrand becomes a polynomial in zn of degree k−1. Use linearity of the integral to integrate the coefficients of the polynomial. Each coefficient is a holomorphic function in V′ and the proof is finished. Some coefficients may have integrated to zero, so we can only say that r is a polynomial of degree k−1 or less.
For example, let f(z,w)=ez+z4ew+zw2ew+zw and P(z,w)=w2+z3. Then P is a Weierstrass polynomial in w of degree k=2. A bit of computation shows 12πi∫∂Dez+z4eζ+zζ2eζ+zζ(ζ2+z3)(ζ−w)dζ=zew,sof(z,w)=(zew)⏟q(w2+z3)⏟P+zw+ez⏟r. Notice that r is a polynomial of degree 1 in w, but it is neither monic, nor do coefficients vanish at 0.
Prove the uniqueness part of the theorem.
State and prove a germ version of the division theorem.
The Weierstrass division theorem is a generalization of the division algorithm for polynomials with coefficients in a field, such as the complex numbers: If f(\zeta) is a polynomial, and P(\zeta) is a nonzero polynomial of degree k, then there exist polynomials q(\zeta) and r(\zeta) with degree of r less than k such that f = qP + r. If the coefficients are in a commutative ring, we can divide as long as P is monic. The Weierstrass division theorem says that in the case of the ring \mathcal{O}_p, we can divide by a monic P \in {}_{n-1}\mathcal{O}_p[z_n], even if f is a holomorphic function (a “polynomial of infinite degree”) as long as f(0,z_n) has finite order.


