6.3: The Dependence of Zeros on Parameters
- Page ID
- 74246
Let us prove that the zeros change holomorphically as long as they do not come together. We will prove shortly that the zeros come together only on a small set; it is a zero set of a certain holomorphic function called the discriminant.
A set of zeros are said to be geometrically distinct if they are distinct points of \(\mathbb{C}\). A zero is called geometrically unique if it is a unique complex number. For example, \({(z_n-1)}^2\) has a geometrically unique zero at \(1\), and \({(z_n-1)}^2(z_n+1)\) has two geometrically distinct zeros, \(1\) and \(-1\).
Let \(D \subset \mathbb{C}\) and \(U' \subset \mathbb{C}^{n-1}\) be domains, and \(f \in \mathcal{O}(U' \times D)\). Suppose that for each fixed \(z' \in U'\) the function \(z_n \mapsto f(z',z_n)\) has a geometrically unique zero \(\alpha(z') \in D\). Then \(\alpha\) is holomorphic in \(U'\).
The proposition shows that the regularity conclusion of the implicit function theorem holds under the hypothesis that there exists some local solution for \(z_n\). This result holds only for holomorphic functions and not for real-analytic functions. For example, \(x^2-y^3 = 0\) has a unique real solution \(y = x^{2/3}\), but that function is not even differentiable.
- Proof
-
We must show that \(\alpha\) is holomorphic near any point, which, without loss of generality, is the origin. Apply the preparation theorem to find \(f = u P\), where \(P\) is a Weierstrass polynomial in \(\mathcal{O}(V')[z_n]\) for some \(V' \subset U'\) and all zeros of \(z_n \mapsto P(z',z_n)\) are in \(D\). As \(\alpha\) is a geometrically unique zero in \(D\), \[P(z',z_n) = {\bigl(z_n-\alpha(z') \bigr)}^k = z_n^k - k \alpha(z') z_n^{k-1} + \cdots\] The coefficients of \(P\) are holomorphic, so \(\alpha\) is holomorphic.
Let \(D \subset \mathbb{C}\) and \(U' \subset \mathbb{C}^{n-1}\) be domains, and \(f \in \mathcal{O}(U' \times D)\). Let \(m \in \mathbb{N}\) be such that for each \(z' \in U'\), the function \(z_n \mapsto f(z',z_n)\) has precisely \(m\) geometrically distinct zeros. Then locally near each point in \(U'\) there exist \(m\) holomorphic functions \(\alpha_1(z'),\ldots,\alpha_m(z')\), positive integers \(k_1,\ldots,k_m\), and a nonvanishing holomorphic function \(u\) such that \[f(z',z_n) = u(z',z_n) \prod_{j=1}^m {\bigl( z_n - \alpha_j(z') \bigr)}^{k_j} .\]
We can only define \(\alpha_1\) through \(\alpha_m\) locally (on a smaller domain) as we do not know how \(\alpha_1\) through \(\alpha_m\) are ordered, and the order could change as we move around \(U'\) if it is not simply connected. If \(U'\) is simply connected, then the functions can be defined globally by analytic continuation. For an example where \(U'\) is not simply connected, recall Example 6.2.1. Consider \(U' = \mathbb{C} \setminus \{ 0 \}\) and think \(D=\mathbb{C}\) rather than a disc for simplicity. Then \(U'\) is not simply connected, and there do not exist continuous functions \(\alpha_1(z_1)\) and \(\alpha_2(z_1)\) that are zeros of the Weierstrass polynomial, that is \(z_2^2 - z_1 = \bigl(z_2-\alpha_1(z_1) \bigr) \bigl(z_2-\alpha_2(z_1) \bigr)\). These would be the two square roots of \(z_1\), and there is no continuous (let alone holomorphic) square root defined in \(\mathbb{C} \setminus \{ 0 \}\). Such roots can be chosen to be holomorphic on any smaller simply connected open subset of \(U'\), for example, on any disc \(\Delta \subset U'\).
Let \(D \subset \mathbb{C}\) be a bounded domain, \(U' \subset \mathbb{C}^{n-1}\) a domain, \(f\) a continuous function on \(U' \times \overline{D}\) holomorphic on \(U' \times D\), where \(f\) is zero on at least one point of \(U' \times D\), and \(f\) is never zero on \(U' \times \partial D\). Suppose that for each fixed \(z' \in U'\) the function \(z_n \mapsto f(z',z_n)\) has at most one zero in \(D\). Prove that for each \(z' \in U'\) \(z_n \mapsto f(z',z_n)\) has exactly one zero in \(D\). Note: And therefore by Proposition \(\PageIndex{1}\), that zero is a holomorphic function.
Prove Proposition \(\PageIndex{2}\). See the exercise above and Proposition \(\PageIndex{1}\).
Let \(D \subset \mathbb{C}\) be a bounded domain, \(U' \subset \mathbb{C}^{n-1}\) a domain, and \(f \in \mathcal{O}(U' \times D)\). Suppose the zero set \(f^{-1}(0)\) has no limit points on \(U' \times \partial D\). Then there exists an \(m \in \mathbb{N}\) and a holomorphic function \(\Delta \colon U' \to \mathbb{C}\), not identically zero, such that for every \(z' \in U' \setminus E\), where \(E = \Delta^{-1}(0)\), \(z_n \mapsto f(z',z_n)\) has exactly \(m\) geometrically distinct zeros in \(D\), and \(z_n \mapsto f(z',z_n)\) has strictly less than \(m\) geometrically distinct zeros for \(z' \in E\).
The complement of a zero set of a holomorphic function is connected, open and dense. The function \(\Delta\) is called the discriminant function and its zero set \(E\) is called the discriminant set. For the quadratic equation, \(\Delta\) is the discriminant we learned about in high school.
- Proof
-
The zeros of \(z_n \mapsto f(z',z_n)\) are isolated, and there are finitely many for every \(z'\) as \(D\) is bounded and \(f^{-1}(0)\) has no limit points on \(U' \times \partial D\). For any \(p' \in U'\) we define two useful paths. Let \(\gamma\) be the union of nonintersecting small simple closed curves in \(D\), one around each geometrically distinct zero of \(z_n \mapsto f(p',z_n)\). Let \(\lambda\) be a large closed path in \(D\) going exactly once around all the zeros and such that the interior of \(\lambda\) is in \(D\). Suppose \(\gamma\) and \(\lambda\) intersect no zeros. See Figure \(\PageIndex{1}\). By continuity, the curves \(\gamma\) and \(\lambda\) do not intersect any zeros for \(z'\) near \(p'\). Since the set \(f^{-1}(0)\) is closed and the zeros do not accumulate on \(U' \times \partial D\), then for \(z'\) near \(p'\) the zeros stay a positive distance away from the boundary. So \(\lambda\) can be picked to go around all the zeros exactly once for \(z'\) near \(p'\).
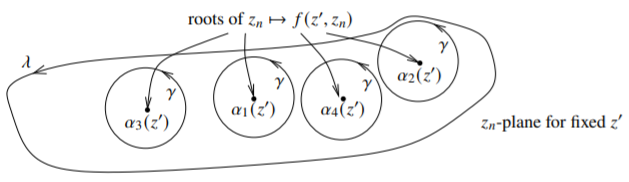
Figure \(\PageIndex{1}\)
The argument principle applied to \(z_n \mapsto f(z',z_n)\) using \(\lambda\) for \(z'\) near \(p'\) shows that the number of zeros (with multiplicity) is bounded by some \(M \in \mathbb{N}\) near \(p'\). The \(M\) is locally well-defined (it does not depend on \(\lambda\) as long as it contains all the zeros), and it is a locally constant function of \(z' \in U'\). As \(U'\) is connected, and it is a fixed number. The maximum number of geometrically distinct zeros must be bounded by \(M\). Let \(m\) be the maximal number of geometrically distinct zeros and suppose that at some point in \(U'\), there are exactly \(m\) geometrically distinct zeros.
Let \(U_m' \subset U'\) be the set of \(z' \in U'\) for which \(z_n \mapsto f(z',z_n)\) has exactly \(m\) zeros. Write \(U'\) as a union of disjoint sets \(U' = U_m' \cup E\), where \(E = U' \setminus U_m'\). By definition of \(m\), \(U_m'\) is nonempty. Suppose \(p' \in U_m'\) and \(\gamma\) goes around the zeros as above. Let \(\gamma'\) be a single component curve of the path \(\gamma\) going around one of the zeros. The argument principle with respect to \(\gamma'\) says that \(\gamma'\) must contain at least one zero for all \(z'\) near \(p'\). There are only finitely many zeros, and so for \(z'\) in some neighborhood of \(p'\), \(z_n \mapsto f(z',z_n)\) has at least \(m\) zeros in \(\gamma\), and as \(m\) is the maximum, it has exactly \(m\) zeros. In other words, \(U_m'\) is open.
Locally on \(U_m'\), there exist \(m\) holomorphic functions \(\alpha_1, \ldots, \alpha_m\) giving the zeros by the previous proposition. We cannot define these on all of \(U_m'\) as we do not know how they are ordered. The function \[\Delta(z') = \prod_{j \not= k} \bigl( \alpha_j(z') - \alpha_k(z') \bigr)\] defined for \(z' \in U_m'\) does not depend on the order. That means \(\Delta\) is well-defined as a function on the open set \(U_m'\), and since \(\alpha_j\) are locally holomorphic, \(\Delta\) is holomorphic.
Let \(p' \in E \cap \overline{U_m'}\), so there are fewer than \(m\) zeros at \(p'\). Suppose \(\gamma\) and \(\lambda\) are as above. In each particular component \(\gamma'\) of \(\gamma\), there must be at least one zero for all \(z'\) near \(p'\) by the same argument as above. There exist \(z'\) arbitrarily near \(p'\) where there are \(m\) zeros. The region between \(\lambda\) and \(\gamma\) (including the curves) is compact, and so by continuity, if \(z_n \mapsto f(p',z_n)\) was nonzero on it, so is \(z_n \mapsto f(z',z_n)\) for \(z'\) near \(p'\). As no zeros of \(z_n \mapsto f(z',z_n)\) lie outside \(\lambda\), we have that all zeros lie in one of the components of \(\gamma\). So if \(z' \in U_m'\) near \(p'\), there must be one component \(\gamma'\) that contains at least two zeros. Let \(\{ z'_\ell \}\) be an arbitrary sequence of points in \(U_m'\) going to \(p'\). As the number of zeros is finite, \(\{ z'_\ell \}\) has a subsequence such that \(z_n \mapsto f(z'_\ell,z_n)\) has at least two zeros in some fixed component \(\gamma'\) of \(\gamma\) for \(z'_\ell\). Assume \(\{ z'_\ell \}\) is this subsequence. Label the two distinct zeros at \(z'_\ell\) as \(\alpha_1(z'_\ell)\) and \(\alpha_2(z'_\ell)\). At \(p'\) there is only a single (geometrically) zero in \(\gamma'\), let us name it \(\alpha_1(p')\). As \(f^{-1}(0)\) is closed it must be that \(\alpha_1(z'_\ell)\) and \(\alpha_2(z'_\ell)\) both approach \(\alpha_1(p')\) as \(\ell \to \infty\). As all zeros are necessarily bounded, \(\lim_{\ell \to \infty} \Delta(z'_\ell) = 0\). As the limit is zero for a subsequence of an arbitrary sequence, \[\lim_{z' \in U_m' \to p'} \Delta(z') = 0 .\]
We have already defined \(\Delta\) on \(U_m'\), so set \(\Delta(z') = 0\) if \(z' \in E\). The function \(\Delta\) is a continuous function on \(U'\) that is zero precisely on \(E\) and holomorphic on \(U_m'\). Radó’s theorem (Theorem 2.4.3) says that \(\Delta\) is holomorphic in \(U'\).
The discriminant given above is really the discriminant of the set \(f^{-1}(0)\) rather than of the corresponding Weierstrass polynomial. Often for Weierstrass polynomials the discriminant is defined as \(\prod_{j \not= k} \bigl( \alpha_j(z') - \alpha_k(z') \bigr)\) taking multiple zeros into account, and therefore the “discriminant” could be identically zero. It will be clear from upcoming exercises that if the Weierstrass polynomial is irreducible, then the two notions do in fact coincide.
Prove that if \(f \in \mathcal{O}(U)\), then \(U \setminus f^{-1}(0)\) is not simply connected if \(f^{-1}(0)\) is nonempty. In particular, in the theorem, \(U' \setminus E\) is not simply connected if \(E \not= \emptyset\).
Let \(D \subset \mathbb{C}\) be a bounded domain, and \(U' \subset \mathbb{C}^{n-1}\) a domain. Suppose \(f\) is a continuous function on \(U' \times \overline{D}\) holomorphic on \(U' \times D\), and \(f\) is never zero on \(U' \times \partial D\). Suppose \(\gamma \colon [0,1] \to U'\) is a continuous function such that \(f\bigl(\gamma(0),c\bigr) = 0\) for some \(c \in D\). Prove that there exists a continuous function \(\alpha \colon [0,1] \to \mathbb{C}\) such that \(\alpha(0) = c\) and \(f\bigl(\gamma(t),\alpha(t)\bigr) = 0\) for all \(t \in [0,1]\). Hint: Show it is possible for a path arbitrarily close to \(\gamma\), but one that stays away from the discriminant.