6.7: Irreducibility, Local Parametrization, and Puiseux Theorem
- Page ID
- 74250
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A germ of a subvariety \((X,p) \subset (\mathbb{C}^n,p)\) is reducible at \(p\) if there exist two germs \((X_1,p)\) and \((X_2,p)\) with \((X_1,p) \not\subset (X_2,p)\) and \((X_2,p) \not\subset (X_1,p)\) such that \((X,p) = (X_1,p) \cup (X_2,p)\). Otherwise, the germ \((X,p)\) is irreducible at \(p\).
Similarly globally, a subvariety \(X \subset U\) is reducible in \(U\) if there exist two subvarieties \(X_1\) and \(X_2\) of \(U\) with \(X_1 \not\subset X_2\) and \(X_2 \not\subset X_1\) such that \(X = X_1 \cup X_2\). Otherwise, the subvariety \(X\) is irreducible in \(U\).
Local and global reducibility are different. The subvariety given by \[z_2^2 = z_1{(z_1-1)}^2 \nonumber\] is irreducible in \(\mathbb{C}^2\) (the regular points are connected), but locally at the point \((1,0)\) it is reducible. There, the subvariety is a union of two graphs: \(z_2 = \pm \sqrt{z_1}(z_1-1)\). See for a plot in two real dimensions.

Figure \(\PageIndex{1}\)
Prove a germ of a subvariety \((X,p)\) is irreducible if and only if \(I_p(X)\) is a prime ideal. Recall an ideal \(I\) is prime if \(ab \in I\) implies either \(a \in I\) or \(b \in I\).
Suppose a germ of a subvariety \((X,p)\) is of pure codimension 1. Prove \((X,p)\) is irreducible if and only if there exists a representative of \(X\), such that \(X_{\textit{reg}}\) is connected.
Let \(X \subset U\) be a subvariety of pure codimension 1 of a domain \(U \subset \mathbb{C}^n\). Prove \(X\) is irreducible if and only if the set of regular points is connected. Hint: See previous exercise.
For complex subvarieties, a subvariety is irreducible if and only if the set of regular points is connected. We omit the proof in the general case, and for hypervarieties it is an exercise above. It then makes sense that we can split a subvariety into its irreducible parts.
Let \((X,p) \subset (\mathbb{C}^n,p)\) be a germ of a subvariety. Then there exist finitely many irreducible subvarieties \((X_1,p),\ldots,(X_k,p)\) such that \((X_1,p) \cup \ldots \cup (X_k,p) = (X,p)\) and such that \((X_j,p) \not\subset (X_\ell,p)\) for all \(j\) and \(\ell\).
- Proof
-
Suppose \((X,p)\) is reducible: Find \((Y_1,p) \not\subset (Y_2,p)\) and \((Y_2,p) \not\subset (Y_1,p)\), such that \((Y_1,p) \cup (Y_2,p) = (X,p)\). As \((Y_j,p) \subsetneq (X,p)\), then \(I_p(Y_j) \supsetneq I_p(X)\) for both \(j\). If both \((Y_1,p)\) and \((Y_2,p)\) are irreducible, then stop, we are done. Otherwise apply the same reasoning to whichever (or both) \((Y_j,p)\) that was reducible. After finitely many steps you must come to a stop as you cannot have an infinite ascending chain of ideals since \(\mathcal{O}_p\) is Noetherian.
These \((X_1,p),\ldots,(X_k,p)\) are the irreducible components. We omit the proof in general that they are unique. For a germ of a hypervariety, the UFD property of \({}_{n}\mathcal{O}_p\) gives the irreducible components. You found this factorization in an exercise above, and so this factorization is unique.
Each irreducible component has the following structure. We give the theorem without proof in the general case, although we have essentially proved it already for pure codimension 1 (to put it together is left as an exercise).
Let \((X,0)\) be an irreducible germ of a subvariety of dimension \(k\) in \(\mathbb{C}^n\). Let \(X\) denote a representative of the germ. Then after a linear change of coordinates, we let \(\pi \colon \mathbb{C}^n \to \mathbb{C}^k\) be the projection onto the first \(k\) components, and obtain that there exists a neighborhood \(U \subset \mathbb{C}^n\) of the origin, and a proper subvariety \(E \subset \pi(U)\) such that
- \(X' = X \cap U \setminus \pi^{-1}(E)\) is a connected \(k\)-dimensional complex manifold that is dense in \(X \cap U\).
- \(\pi \colon X' \to \pi(U) \setminus E\) is an \(m\)-sheeted covering map for some integer \(m\).
- \(\pi \colon X \cap U \to \pi(U)\) is a proper mapping.
The \(m\)-sheeted covering map in this case is a local biholomorphism that is an \(m\)-to-1 map.
Use Theorem 6.3.1 to prove the parametrization theorem if \((X,0)\) is of pure codimension 1.
Let \((z_1,\ldots,z_n)\) be the coordinates. The linear change of coordinates needed in the theorem is to ensure that the set defined by \(z_1=z_2=\cdots=z_k = 0\) intersected with \(X\) is an isolated point at the origin. This is precisely the same condition needed to apply Weierstrass preparation theorem in the case when \(X\) is the zero set of a single function.
We saw hypersurfaces are the simpler cases of complex-analytic subvarieties. At the other end of the spectrum, complex-analytic subvarieties of dimension 1 are also reasonably simple for different reasons. Locally, complex-analytic subvarieties of dimension 1 are analytic discs. Moreover, they are locally the one-to-one holomorphic images of discs, and so they have a natural topological manifold structure even at singular points.
The image of the analytic disc \(\xi \mapsto (\xi^2,\xi^3)\) is the cusp subvariety defined by \(z_1^3-z_2^2 = 0\) in \(\mathbb{C}^2\).
The following theorem is often stated only in \(\mathbb{C}^2\) for zero sets of a single function although it follows in the same way from the local parametrization theorem in higher-dimensional spaces. Of course, we only proved that theorem (or in fact you the reader did so in an exercise), for codimension 1 subvarieties, and therefore, we also only have a complete proof of the following in \(\mathbb{C}^2\).
Let \((z,w) \in \mathbb{C} \times \mathbb{C}^{n-1}\) be coordinates. Suppose \(f \colon U \subset \mathbb{C} \times \mathbb{C}^{n-1} \to \mathbb{C}^\ell\) is a holomorphic map such that \(f(z,w) = 0\) defines a dimension 1 subvariety \(X\) of \(U\), \(0 \in X\), and \(w \mapsto f(0,w)\) has an isolated zero at the origin.
Then there exists an integer \(k\) and a holomorphic function \(g\) defined near the origin in \(\mathbb{C}\) such that for all \(\xi\) near the origin \[f\bigl(\xi^k,g(\xi)\bigr) = 0 .\]
- Proof
-
Without loss of generality assume \((X,0)\) is irreducible, so that the local parametrization theorem applies. We work in a small disc \(D \subset \mathbb{C}\) centered at the origin, such that the origin is the unique point of the discriminant set (the subvariety \(E\)). Let \(N = \{ z \in D : \Im z = 0 , \Re z \leq 0 \}\). As \(D \setminus N\) is simply connected we have the well-defined functions \(\alpha_1(z),\ldots,\alpha_m(z)\) holomorphic on \(D \setminus N\) that are solutions to \(f\bigl(z,\alpha_j(z)\bigr) = 0\). These functions continue analytically across \(N\) away from the origin. The continuation equals one of the zeros, e.g. \(\alpha_j(z)\) becomes \(\alpha_\ell(z)\) (and by continuity it is the same zero along the entire \(N\)). So there is a permutation \(\sigma\) on \(m\) elements such that as \(z\) moves counter-clockwise around the origin from the upper half-plane across \(N\) to the lower half-plane, \(\alpha_j(z)\) is continued as \(\alpha_{\sigma(j)}(z)\). There exists some number \(k\) (e.g. \(k=m!\)) such that \(\sigma^k\) is the identity. As \(\xi\) goes around a circle around the origin, \(\xi^k\) goes around the origin \(k\) times. Start at a positive real \(\xi\) and start defining a function \(g(\xi)\) as \(\alpha_1(\xi^k)\). Move \(\xi\) around the origin counter-clockwise continuing \(g\) analytically. Divide the disc into sectors of angle \(\frac{2\pi}{k}\), whose boundaries are where \(\xi^k \in N\). Transition to \(\alpha_{\sigma(1)}(\xi^k)\) after we reach the boundary of the first sector, then to \(\alpha_{\sigma(\sigma(1))}(\xi^k)\) after we reach the boundary of the next sector, and so on. After \(k\) steps, that is as \(\xi\) moved all the way around the circle, we are back at \(\alpha_1(\xi^k)\), because \(\sigma^k\) is the identity. So \(g(\xi)\) is a well-defined holomorphic function outside the origin. Let \(g(0) = 0\), and \(g\) is holomorphic at 0 by the Riemann extension theorem. See Figure \(\PageIndex{2}\) for an example.
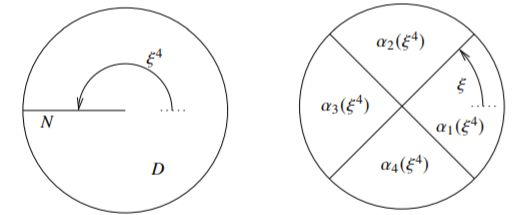
In the figure, \(m=k=4\), and the permutation \(\sigma\) takes \(1\) to \(2\), \(2\) to \(3\), \(3\) to \(4\), and \(4\) to \(1\). As \(\xi\) moves along the short circular arrow on the right, \(\xi^{4}\) moves along the long circular arrow on the left. The definition of \(g\) is then given in the right-hand diagram.
Consider an irreducible germ \((X,0) \subset (\mathbb{C}^2,0)\) defined by an irreducible Weierstrass polynomial \(f(z,w) = 0\) (polynomial in \(w\)) of degree \(k\). Prove there exists a holomorphic \(g\) such that \(f\bigl(z^k,g(z)\bigr) = 0\) and \(z \mapsto \bigl(z^k,g(z)\bigr)\) is one-to-one and onto a neighborhood of 0 in \(X\).
Suppose \((X,0) \subset (\mathbb{C}^2,0)\) is a germ of a dimension 1 subvariety. Show that after perhaps a linear change of coordinates, there are natural numbers \(d_1,\ldots,d_k\) and holomorphic functions \(c_1(z),\ldots,c_k(z)\) vanishing at \(0\), such that \(X\) can be defined near 0 by \[\prod_{j=1}^k {\bigl( w^{d_j} - c_j(z) \bigr)} = 0.\]
Using the local parametrization theorem, prove that if \((X,p)\) is an irreducible germ of a subvariety of dimension greater than 1, then there exists a neighborhood \(U\) of \(p\) and a closed subvariety \(X \subset U\) (whose germ at \(p\) is \((X,p)\)), such that for every \(q \in X\) there exists an irreducible subvariety \(Y \subset X\) of dimension 1 such that \(p \in Y\) and \(q \in Y\).
Prove a stronger version of the exercise above. Show that not only is there a \(Y\), but an analytic disc \(\varphi \colon \mathbb{D} \to U\) such that \(\varphi(\mathbb{D}) \subset X\), \(\varphi(0) = p\) and \(\varphi(\frac{1}{2}) = q\).
Suppose \(X \subset U\) is a subvariety of a domain \(U \subset \mathbb{C}^n\). Suppose that for any two points \(p\) and \(q\) on \(X\) there exists a finite sequence of points \(p_0 = p, p_1, \ldots, p_k = q\) in \(X\), and a sequence of analytic discs \(\Delta_j \subset X\) such that \(p_{j}\) and \(p_{j-1}\) are in \(\Delta_j\).
Prove a maximum principle for subvarieties using the exercises above: Suppose \(X \subset U\) is an irreducible subvariety of an open set \(U\), and suppose \(f \colon U \to \mathbb{R} \cup \{ - \infty \}\) is a plurisubharmonic function. If the modulus of the restriction \(f|_X\) achieves a maximum at some point \(p \in X\), then the restriction \(f|_X\) is constant.
Prove that an analytic disc (namely the image of the disc) in \(\mathbb{C}^2\) is a one-dimensional local variety (that is, a subvariety of some open subset of \(\mathbb{C}^2\)).
Using the Puiseux theorem, we often simply parametrize germs of complex one-dimensional subvarieties. And for larger-dimensional varieties, we can find enough one-dimensional curves through any point and parametrize those.


