6.8: Segre Varieties and CR Geometry

The existence of analytic discs (or subvarieties) in boundaries of domains says a lot about the geometry of the boundary.

Example \(\PageIndex{1}\)

Let \(M \subset \mathbb{C}^n\) be a smooth real hypersurface containing a complex hypersurface \(X\) (zero set of a holomorphic function with nonzero derivative), at \(p \in X \subset M\). Apply a local biholomorphic change of coordinates at \(p\), so that in the new coordinates \((z,w) \in \mathbb{C}^{n-1} \times \mathbb{C}\), \(X\) is given by \(w=0\), and \(p\) is the origin. The tangent hyperplane to \(M\) at 0 contains \(\{ w=0 \}\). By rotating the \(w\) coordinate (multiplying it by \(e^{i\theta}\)), we assume \(M\) is tangent to the set \(\bigl\{ (z,w) : \Im w = 0 \bigr\}\). In other words, \(M\) is given by \[\Im w = \rho(z,\bar{z},\Re w) ,\] where \(d\rho = 0\). As \(w = 0\) on \(M\), then \(\rho = 0\) when \(\Re w = 0\). That is, \(\rho\) is divisible by \(\Re w\). So \(M\) is defined by \[\Im w = (\Re w) \widetilde{\rho}(z,\bar{z},\Re w),\] for a smooth function \(\widetilde{\rho}\). The Levi form at the origin vanishes. As \(p=0\) was an arbitrary point on \(M \cap X\), the Levi form of \(M\) vanishes on \(M \cap X\).

Example \(\PageIndex{2}\)

The vanishing of the Levi form is not necessary if the complex varieties in \(M\) are small. Consider \(M\subset \mathbb{C}^3\) with a nondegenerate (but not definite) Levi form: \[\Im w = |z_1|^2-|z_2|^2 .\] For every \(\theta \in \mathbb{R}\), \(M\) contains the complex line \(L_\theta\), given by \(z_1 = e^{i\theta} z_2\) and \(w = 0\). The union \(\bigcup_\theta L_\theta\) of those complex lines is not contained in some single unique complex subvariety inside \(M\). Any complex subvariety that contains all \(L_\theta\) must contain the entire complex hypersurface given by \(w = 0\), which is not contained in \(M\).

Exercise \(\PageIndex{1}\)

Let \(M \subset \mathbb{C}^n\) be a smooth real hypersurface. Show that if \(M\) at \(p\) contains a complex submanifold of (complex) dimension more than \(\frac{n-1}{2}\), then the Levi form must be degenerate, that is, it must have at least one zero eigenvalue.

Exercise \(\PageIndex{2}\)

Let \(M \subset \mathbb{C}^n\) be a smooth pseudoconvex real hypersurface (one side of \(M\) is pseudoconvex). Suppose \(M\) at \(p\) contains a dimension \(k\) complex submanifold \(X\). Show that the Levi form has at least \(k\) zero eigenvalues.

Exercise \(\PageIndex{3}\)

Find an example of a smooth real hypersurface \(M \subset \mathbb{C}^n\) that contains a germ of a singular complex-analytic subvariety \((X,p)\) through a point \(p\), which is unique in the sense that if \((Y,p)\) is another germ of a complex analytic subvariety in \(M\) then \((Y,p) \subset (X,p)\).

Let us discuss a tool, the Segre variety, that allows us to find such complex subvarieties inside \(M\), and much more. Segre varieties only work in the real-analytic setting and rely on complexification.

Let \(M \subset \mathbb{C}^n\) be a real-analytic hypersurface and \(p \in M\). Suppose \(M \subset U\), where \(U \subset \mathbb{C}^n\) is a small domain with a defining function \(r \colon U \to \mathbb{R}\) for \(M\). That is, \(r\) is a real-analytic function in \(U\) such that \(M = r^{-1}(0)\), but \(dr \not= 0\) on \(M\). Define \[U^* = \bigl\{ z \in \mathbb{C}^n : \bar{z} \in U \bigr\} .\] Suppose \(U\) is small enough so that the Taylor series for \(r\) converges in \(U \times U^*\) when treating \(z\) and \(\bar{z}\) as separate variables. That is, \(r(z,\zeta)\) is a well-defined function on \(U \times U^*\), and \(r(z,\zeta) = 0\) defines a complexification \(\mathcal{M}\) in \(U \times U^*\). Assume also that \(U\) is small enough that the complexified \(dr\) does not vanish on \(\mathcal{M}\) and that \(\mathcal{M}\) is connected. See also Proposition 3.2.3.

Given \(q \in U\), define the Segre variety \[\Sigma_q(U,r) = \bigl\{ z \in U : r(z,\bar{q}) = 0 \bigr\} = \bigl\{ z \in U : (z,\bar{q}) \in \mathcal{M} \bigr\} .\] A priory, the subvariety \(\Sigma_p\) depends on \(U\) and \(r\). However, if \(\widetilde{r}\) is a real-analytic function that complexifies to \(U \times U^*\) and vanishes on \(M\), it must also vanish on the complexification \(\mathcal{M}\). If \(\widetilde{r}\) is a defining function as above, that is, \(d\widetilde{r}\) does not vanish on its zero set and the zero set of the complexified \(\widetilde{r}\) is connected in \(U \times U^*\), then \(\widetilde{r}(z,\zeta) = 0\) also defines \(\mathcal{M}\). Hence the actual \(r\) does not matter. As long as \(q \in M\), then \(q \in \Sigma_q(U,r)\), and furthermore the Segre variety is a complex hypersurface for every \(q\). It is not hard to see that if \(\widetilde{U}\) is a small neighborhood of \(q\), the same \(r\) is a defining function in \(\widetilde{U}\), and we get the same complexification in \(\widetilde{U} \times \widetilde{U}^*\). So the germ at \(q \in U\) is well-defined, and we write \[\Sigma_q = \bigl( \Sigma_q(U,r) , q \bigr) .\] The Segre variety is well-defined as a germ, and so often when one talks about \(\Sigma_q\) without mentioning the \(U\) or \(r\), then one means some small enough representative of a Segre variety or the germ itself.

Exercise \(\PageIndex{4}\)

Let \(r \colon U \to \mathbb{R}\) be a real-valued real-analytic function that complexifies to \(U \times U^*\). Show that \(r(z,\bar{\zeta}) = 0\) if and only if \(r(w,\bar{\zeta}) = 0\). In other words, \(z \in \Sigma_{\zeta}(U,r)\) if and only if \(\zeta \in \Sigma_z(U,r)\).

Example \(\PageIndex{3}\)

Suppose we start with the real-analytic hypersurface \(M\) given by \[\Im w = (\Re w) \rho(z,\bar{z},\Re w) ,\] with \(\rho\) vanishing at the origin. Rewriting in terms of \(w\) and \(\bar{w}\), we find \[\frac{w-\bar{w}}{2i} = \left(\frac{w+\bar{w}}{2}\right) \rho\left(z,\bar{z},\frac{w+\bar{w}}{2}\right) .\] Setting \(\bar{z} = \bar{w} = 0\), we obtain \[\frac{w}{2i} = \left(\frac{w}{2}\right) \rho\left(z,0,\frac{w}{2}\right) .\] As \(\rho\) vanishes at the origin, then near the origin the equation defines the complex hypersurface given by \(w=0\). So \(\Sigma_0\) is defined by \(w = 0\). This is precisely the complex hypersurface that lies inside \(M\).

The last example is not a fluke. The most important property of Segre varieties is that it locates complex subvarieties in a real-analytic submanifold. We will phrase it in terms of analytic discs, which is enough as complex subvarieties can be filled with analytic discs, as we have seen.

Proposition \(\PageIndex{1}\)

Let \(M \subset \mathbb{C}^n\) be a real-analytic hypersurface and \(p \in M\). Suppose \(\Delta \subset M\) is an analytic disc through \(p\). Then as germs \((\Delta,p) \subset \Sigma_p\).

Proof

Let \(U\) be a neighborhood of \(p\) where a representative of \(\Sigma_p\) is defined, that is, we assume that \(\Sigma_p\) is a closed subset of \(U\), and suppose \(r(z,\bar{z})\) is the corresponding defining function. Let \(\varphi \colon \mathbb{D} \to \mathbb{C}^n\) be the parametrization of \(\Delta\) with \(\varphi(0) = p\). We can restrict \(\varphi\) to a smaller disc around the origin, and since we are only interested in the germ of \(\Delta\) at \(p\) this is sufficient (if there are multiple points of \(\mathbb{D}\) that go to \(p\), we repeat the argument for each one). So let us assume without loss of generality that \(\varphi(\mathbb{D}) = \Delta \subset U\). Since \(\Delta \subset M\) we have \[r\bigl(\varphi(\xi),\overline{\varphi(\xi)}\bigr) = r\bigl(\varphi(\xi),\bar{\varphi}(\bar{\xi})\bigr) = 0 .\] The function \(\xi \mapsto r\bigl(\varphi(\xi),\bar{\varphi}(\bar{\xi})\bigr)\) is a real-analytic function of \(\xi\), and therefore for some small neighborhood of the origin, it complexifies. In fact, it complexifies to \(\mathbb{D} \times \mathbb{D}\) as \(\varphi(\xi) \in U\) for all \(\xi \in \mathbb{D}\). So we can treat \(\xi\) and \(\bar{\xi}\) as separate variables. By complexification, the equation holds for all such independent \(\xi\) and \(\bar{\xi}\). Set \(\bar{\xi} = 0\) to obtain \[0 = r\bigl(\varphi(\xi),\bar{\varphi}(0)\bigr) = r\bigl(\varphi(\xi),\bar{p}\bigr) \qquad \text{for all $\xi \in \mathbb{D}$}.\] In particular, \(\varphi(\mathbb{D}) \subset \Sigma_p\) and the result follows.

Exercise \(\PageIndex{5}\)

Show that if a real-analytic real hypersurface \(M \subset \mathbb{C}^n\) is strongly pseudoconvex at \(p \in M\) (one side of \(M\) is strongly pseudoconvex at \(p\)), then \(\Sigma_p \cap (M,p) = \{p\}\) (as germs).

Exercise \(\PageIndex{6}\)

Use the proposition and the exercise above to show that if a real-analytic real hypersurface \(M\) is strongly pseudoconvex, then \(M\) contains no analytic discs.

We end our discussion of Segre varieties by its perhaps most well-known application, the so-called Diederich–Fornæss lemma. Although we state and prove it only for real-analytic hypersurfaces it works in greater generality. There are two parts to it, although it is generally the corollary that is called the Diederich-Fornæss lemma.

First, for real-analytic hypersurfaces each point has a fixed neighborhood such that germs of complex subvarieties contained in the hypersurface extend to said fixed neighborhood.

Theorem \(\PageIndex{1}\)

Diederich–Fornæss

Suppose \(M \subset \mathbb{C}^n\) is a real-analytic hypersurface. For every \(p \in M\) there exists a neighborhood \(U\) of \(p\) with the following property: If \(q \in M \cap U\) and \((X,q)\) is a germ of a complex subvariety such that \((X,q) \subset (M,q)\), then there exists a complex subvariety \(Y \subset U\) (in particular a closed subset of \(U\)) such that \(Y \subset M\) and \((X,q) \subset (Y,q)\).

Proof

Suppose \(U\) is a polydisc centered at \(p\), small enough so that the defining function \(r\) of \(M\) complexifies to \(U \times U^*\) as above. Suppose \(q \in M \cap U\) is a point such that \((X,q)\) is a germ of a positive-dimensional complex subvariety with \((X,q) \subset (M,q)\). Most points of a subvariety are regular, so without loss of generality assume \(q\) is a regular point, that is, \((X,q)\) is a germ of a complex submanifold. Let \(X\) be a representative of the germ \((X,q)\) such that \(X \subset M\), and \(X \subset U\), although we do not assume it is closed.

Assume \(X\) is an image of an open subset \(V \subset \mathbb{C}^k\) via a holomorphic surjective mapping \(\varphi \colon V \to X\). Since \(r\bigl(\varphi(\xi),\overline{\varphi(\xi)}\bigr) = 0\) for all \(\xi \in V\), then we may treat \(\xi\) and \(\bar{\xi}\) separately. In particular, \(r(z,\bar{\zeta}) = 0\) for all \(z,\zeta \in X\).

Define complex subvarieties \(Y', Y \subset U\) (closed in \(U\)) by \[Y' = \bigcap_{a \in X} \Sigma_a(U,r) \qquad \text{and} \qquad Y = \bigcap_{a \in Y'} \Sigma_a(U,r) .\] If \(a \in Y'\) and \(b \in X\), then \(r(a,\bar{b}) = 0\). Because \(r\) is real-valued, \(r(b,\bar{a}) = 0\). Therefore, \(X \subset Y \subset Y'\). Furthermore, \(r(z,\bar{z}) = 0\) for all \(z \in Y\), and so \(Y \subset M\).

Corollary \(\PageIndex{1}\)

Diederich-Fornæss

Suppose \(M \subset \mathbb{C}^n\) is a compact real-analytic hypersurface. Then there does not exist any point \(q \in M\) such that there exists a germ of a positive-dimensional complex subvariety \((X,q)\) such that \((X,q) \subset (M,q)\).

Proof

Let \(S \subset M\) be the set of points through which there exists a germ of a positive-dimensional complex subvariety contained in \(M\). As \(M\), and hence \(\overline{S}\), is compact, there must exist a point \(p \in \overline{S}\) that is furthest from the origin. After a rotation by a unitary and rescaling assume \(p=(1,0,\ldots,0)\). Let \(U\) be the neighborhood from the previous theorem around \(p\). There exist germs of varieties in \(M\) through points arbitrarily close to \(p\). So for any distance \(\epsilon > 0\), there exists a subvariety \(Y \subset U\) (in particular, \(Y\) closed in \(U\)) of positive dimension with \(Y \subset M\) that contains points \(\epsilon\) close to \(p\). Consider the function \(\Re z_1\), whose modulus attains a strict maximum on \(\overline{S}\) at \(p\). Because \(\Re z_1\) achieves a maximum strictly smaller than 1 on \(\partial U \cap \overline{S}\), for a small enough \(\epsilon\), we would obtain a pluriharmonic function with a strict maximum on \(Y\), which is impossible by the maximum principle for varieties that you proved in Exercise 6.7.10. The picture would look as in Figure \(\PageIndex{1}\).

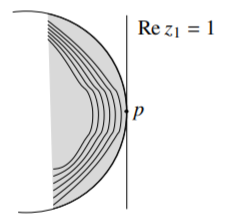
Figure \(\PageIndex{1}\)

Example \(\PageIndex{4}\)

The results above do not work in the smooth setting. Let us disprove the theorem in the smooth setting. Disproving the corollary is an exercise. Let \(g \colon \mathbb{R} \to \mathbb{R}\) be a smooth function that is strictly positive for \(|t| > 1\), and \(g(t) = 0\) for all \(|t| \leq 1\). Define \(M\) in \((z,w) \in \mathbb{C}^{n-1} \times \mathbb{C}\) by \[\Im w = g\bigl(||z||^2 + (\Re w)^2\bigr) .\] The \(M\) is a smooth real hypersurface. Consider \(p = (0,\ldots,0,1) \in M\). For every \(0 < s < 1\), let \(q_s = (0,\ldots,0,s) \in M\) and \(X_s = \bigl\{ (z,w) \in M : w = s \bigr\}\). Each \(X_s\) is the closure of a local complex subvariety of dimension \(n-1\) and \((X_s,q_s) \subset (M,q_s)\). The size (diameter) of \(X_s\) goes to zero as \(s \to 1\) and \(X_s\) cannot extend to a larger complex subvariety inside \(M\). So, no neighborhood \(U\) at \(p\) (as in the theorem) exists.

Exercise \(\PageIndex{7}\)

Find a compact smooth real hypersurface \(M \subset \mathbb{C}^n\) that contains a germ of a positive dimensional complex subvariety.

…and that is how using sheep’s bladders can prevent earthquakes!