9.1: Binomial Probability

Learning Objectives

In this section, you will learn to:

1. Recognize when to use the binomial probability distribution
2. Derive the formula for the binomial probability distribution
3. Calculate probabilities for a binomial probability experiment

In this section, we consider problems that involve a sequence of trials, where each trial has only two outcomes, a success or a failure. These trials are independent, that is, the outcome of one does not affect the outcome of any other trial. The probability of success, \(p\), and the probability of failure, \((1 - p)\), remains the same throughout the experiment. These problems are called binomial probability problems. Since these problems were researched by Swiss mathematician Jacques Bernoulli around 1700, they are also called Bernoulli trials.

We give the following definition:

Binomial Experiment

A binomial experiment satisfies the following four conditions:

1. There are only two outcomes, a success or a failure, for each trial.
2. The same experiment is repeated several times.
3. The trials are independent; that is, the outcome of a particular trial does not affect the outcome of any other trial.
4. The probability of success remains the same for every trial.

This probability model that will give us the tools to solve many real-life problems , such as:

1. If a coin is flipped 10 times, what is the probability that it will fall heads 3 times?
2. If a basketball player makes 3 out of every 4 free throws, what is the probability that he will make 7 out of 10 free throws in a game?
3. If a medicine cures 80% of the people who take it, what is the probability that among the ten people who take the medicine, 6 will be cured?
4. If a microchip manufacturer claims that only 4% of his chips are defective, what is the probability that among the 60 chips chosen, exactly three are defective?
5. If a telemarketing executive has determined that 15% of the people contacted will purchase the product, what is the probability that among the 12 people who are contacted, 2 will buy the product?

We now consider the following example to develop a formula for finding the probability of \(k\) successes in \(n\) Bernoulli trials.

Example \(\PageIndex{1}\)

A baseball player has a batting average of .300. If he bats four times in a game, find the probability that he will have

1. 4 hits
2. 3 hits
3. 2 hits
4. 1 hit
5. no hits.

Solution

Let S denote that the player gets a hit, and F denote that he does not get a hit.

This is a binomial experiment because it meets all four conditions. First, there are only two outcomes, S or F. Clearly the experiment is repeated four times. Lastly, if we assume that the player's skillfulness to get a hit does not change each time he comes to bat, the trials are independent with a probability of .3 of getting a hit during each trial.

We draw a tree diagram to show all situations.

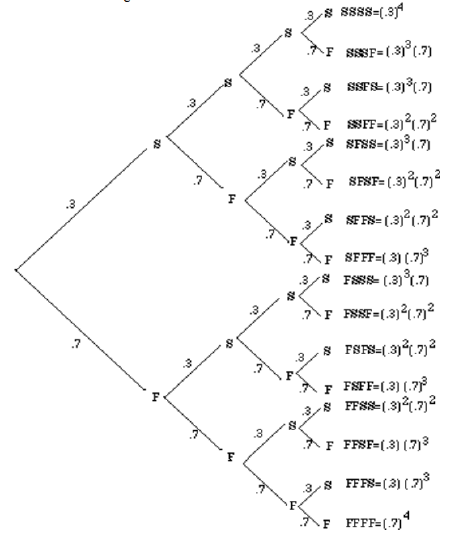
Let us first find the probability of getting, for example, two hits. We will have to consider the six possibilities, SSFF, SFSF, SFFS, FSSF, FSFS, FFSS, as shown in the above tree diagram. We list the probabilities of each below.

\[\begin{array}{l}
\mathrm{P}(\mathrm{SSFF})=(.3)(.3)(.7)(.7)=(.3)^{2}(.7)^{2} \\
\mathrm{P}(\mathrm{SFSF})=(.3)(.7)(.3)(.7)=(.3)^{2}(.7)^{2} \\
\mathrm{P}(\mathrm{SFFS})=(.3)(.7)(.7)(.3)=(.3)^{2}(.7)^{2} \\
\mathrm{P}(\mathrm{FSSF})=(.7)(.3)(.3)(.7)=(.3)^{2}(.7)^{2} \\
\mathrm{P}(\mathrm{FSFS})=(.7)(.3)(.7)(.3)=(.3)^{2}(.7)^{2} \\
\mathrm{P}(\mathrm{FFSS})=(.7)(.7)(.3)(.3)=(.3)^{2}(.7)^{2}
\end{array} \nonumber \]

Since the probability of each of these six outcomes is \((.3)^2(.7)^2\), the probability of obtaining two successes is \(6(.3)^2(.7)^2\).

The probability of getting one hit can be obtained in the same way. Since each permutation has one S and three F's, there are four such outcomes: SFFF, FSFF, FFSF, and FFFS.

And since the probability of each of the four outcomes is \((.3)(.7)^3\), the probability of getting one hit is \(4(.3)(.7)^3\).

The table below lists the probabilities for all cases, and shows a comparison with the binomial expansion of fourth degree. Again, \(p\) denotes the probability of success, and \(q = (1 - p)\) the probability of failure.

Outcome	Four Hits	Three Hits	Two Hits	One Hit	No Hits
Probability	\((.3)^4\)	\(4 (.3)^3(.7)\)	\(6 (.3)^2(.7)^2\)	\(4 (.3)(.7)^3\)	\((.7)^4\)

\[\begin{array}{l}
(.3+.7)^{4}=(.3)^{4}+4(.3)^{3}(.7)+6(.3)^{2}(.7)^{2}+4(.3)(.7)^{3}+(.7)^{4} \\
(p+q)^{4}=p^{4}+4 p^{3} q+6 p^{2} q^{2}+4 p q^{3}+q^{4}
\end{array} \nonumber \]

This gives us the following theorem:

Binomial Probability Theorem

The probability of obtaining \(k\) successes in \(n\) independent Bernoulli trials is given by

\[ \mathbf{P}(\mathbf{n}, \mathbf{k} ; \mathbf{p})=\mathbf{n} \mathbf{C} \mathbf{k} \: \mathbf{p}^{\mathbf{k}} \mathbf{q}^{\mathbf{n}-\mathbf{k}} \nonumber \]

where \(p\) denotes the probability of success and \(q = (1 - p) \) the probability of failure.

We use the binomial probability formula to solve the following examples.

Example \(\PageIndex{2}\)

If a coin is flipped 10 times, what is the probability that it will fall heads 3 times?

Solution

Let S denote the probability of obtaining a head, and F the probability of getting a tail.

Clearly, \(n = 10\), \(k = 3\), \(p = 1/2\), and \(q = 1/2\).

Therefore, \(\mathrm{b}(10,3 ; 1 / 2)=10 \mathrm{C} 3 \: (1 / 2)^{3}(1 / 2)^{7}=.1172\)

Example \(\PageIndex{3}\)

If a basketball player makes 3 out of every 4 free throws, what is the probability that he will make 6 out of 10 free throws in a game?

Solution

The probability of making a free throw is 3/4.
Therefore, \(p = 3/4\), \(q = 1/4\), \(n = 10\), and \(k = 6\).

Therefore, \(b(10, 6; 3/4) = 10\mathrm{C}6 \: (3/4)^6(1/4)^4 = .1460\)

Example \(\PageIndex{4}\)

If a medicine cures 80% of the people who take it, what is the probability that of the eight people who take the medicine, 5 will be cured?

Solution

Here \(p =.80\), \(q = .20\), \(n = 8\), and \(k = 5\).

\[ b(8, 5; .80) = 8\mathrm{C}5 \: (.80)^5(.20)^3 = .1468 \nonumber \]

Example \(\PageIndex{5}\)

If a microchip manufacturer claims that only 4% of his chips are defective, what is the probability that among the 60 chips chosen, exactly three are defective?

Solution

If S denotes the probability that the chip is defective, and F the probability that the chip is not defective, then \(p = .04\), \(q = .96\), \(n = 60\), and \(k = 3\).

\[ b(60, 3; .04) = 60 \mathrm{C} 3 \: (.04)^3(.96)^{57} = .2138 \nonumber \]

Example \(\PageIndex{6}\)

A telemarketing executive has determined that 15% of people contacted will purchase the product. 12 people are contacted about this product.

1. Find the probability that among 12 people contacted, 2 will buy the product.
2. Find the probability that among 12 people contacted, at most 2 will buy the product?

Solution

a. If S denoted the probability that a person will buy the product, and F the probability that the person will not buy the product, then \(p = .15\), \(q = .85\), \(n = 12\), and \(k = 2\).

\[b(12, 2; .15) = 12 \mathrm{C} 2 \: (.15)^2(.85)^{10} = .2924 \nonumber. \nonumber \]

The probability that 2 people buy the product is 0.2924.

b. Again \(p = .15\), \(q = .85\), \(n = 12\). But to find the probability that at most 2 buy the product, we need to find the probabilities for \(k= 0\), \(k=1\), \(k=2\) and add them together.

\[\begin{array}{l}
\mathrm{b}(12,0; .15)=12 \mathrm{C} 0 \: (.15)^{0}(.85)^{12}=.1422 \\
\mathrm{b}(12,1; .15)=12 \mathrm{C} 1 \: (.15)^{1}(.85)^{11}=.3012
\end{array} \nonumber \]

Adding all three probabilities gives: .1422 +0.3012 +.2924 = .7358

The probability that at most 2 people buy the product is 0.7358.