9.4: Probability Using Tree Diagrams

Last updated
Save as PDF

Page ID: 37922

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

In this section, you will learn to:

Use probability trees to organize information in probability problems
Use probability trees to calculate probabilities

As we have already seen, tree diagrams play an important role in solving probability problems. A tree diagram helps us not only visualize, but also list all possible outcomes in a systematic fashion. Furthermore, when we list various outcomes of an experiment and their corresponding probabilities on a tree diagram, we gain a better understanding of when probabilities are multiplied and when they are added.

The meanings of the words and and or become clear when we learn to multiply probabilities horizontally across branches, and add probabilities vertically down the tree.

Although tree diagrams are not practical in situations where the possible outcomes become large, they are a significant tool in breaking the problem down in a schematic way. We consider some examples that may seem difficult at first, but with the help of a tree diagram, they can easily be solved.

Example $\PageIndex{1}$

A person has four keys and only one key fits to the lock of a door. What is the probability that the locked door can be unlocked in at most three tries?

Solution

Let U be the event that the door has been unlocked and L be the event that the door has not been unlocked. We illustrate with a tree diagram.

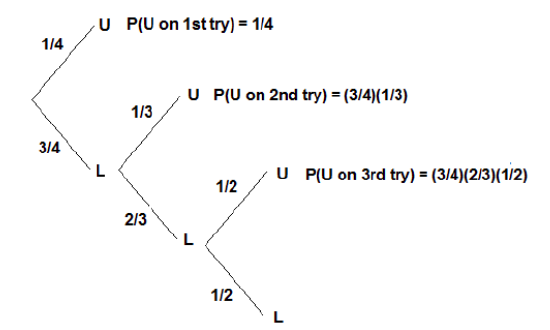
$Example9.4.1.png$

The probability of unlocking the door in the first try = 1/4

The probability of unlocking the door in the second try = (3/4)(1/3) = 1/4

The probability of unlocking the door in the third try = (3/4)(2/3)(1/2) = 1/4

Therefore, the probability of unlocking the door in at most three tries = 1/4 + 1/4 + 1/4 = 3/4.

Example $\PageIndex{2}$

A jar contains 3 black and 2 white marbles. We continue to draw marbles one at a time until two black marbles are drawn. If a white marble is drawn, the outcome is recorded and the marble is put back in the jar before drawing the next marble. What is the probability that we will get exactly two black marbles in at most three tries?

Solution

We illustrate using a tree diagram.

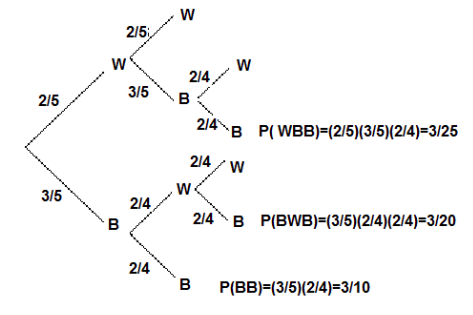
$Example9.4.2.png$

The probability that we will get two black marbles in the first two tries is listed adjacent to the lowest branch, and it = 3/10.

The probability of getting first black, second white, and third black = 3/20.

Similarly, the probability of getting first white, second black, and third black = 3/25.

Therefore, the probability of getting exactly two black marbles in at most three tries = 3/10 + 3/20 + 3/25 = 57/100.

Example $\PageIndex{3}$

A circuit consists of three resistors: resistor $R_1$, resistor $R_2$, and resistor $R_3$, joined in a series. If one of the resistors fails, the circuit stops working. The probabilities that resistors $R_1$, $R_2$, or $R_3$ will fail are .07, .10, and .08, respectively. Find the probability that at least one of the resistors will fail?

Solution

The probability that at least one of the resistors fails = 1 - none of the resistors fails.

It is quite easy to find the probability of the event that none of the resistors fails.
We don't even need to draw a tree because we can visualize the only branch of the tree that assures this outcome.

The probabilities that $R_1$, $R_2$, $R_3$ will not fail are .93, .90, and .92 respectively. Therefore, the probability that none of the resistors fails = (.93)(.90)(.92) = .77.

Thus, the probability that at least one of them will fail = 1 - .77 = .23.

Learning Objectives

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)