10.2.1: Applications of Markov Chains (Exercises)

Last updated
Save as PDF

Page ID: 37935

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

SECTION 10.2 PROBLEM SET: APPLICATIONS OF MARKOV CHAINS

Questions 1-2 refer to the following:

Reference: Bart Sinclair, Machine Repair Model. OpenStax CNX. Jun 9, 2005 Creative Commons Attribution License 1.0. Download for free at http://cnx.org/contents/56f1bed0-bd34-4c28-a2ec-4a3f9ded8e18@3. This material has been modified by Roberta Bloom, as permitted under that license.

A Markov chain can be used to model the status of equipment, such as a machine used in a manufacturing process. Suppose that the possible states for the machine are

Idle & awaiting work (I) Working on a job/task (W) Broken (B) In Repair (R)

The machine is monitored at regular intervals to determine its status; for ease of interpretation in this problem, we assume the status is monitored every hour. The transition matrix is shown below:

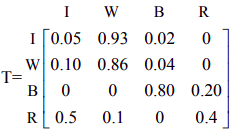
$Section10.5.2.png$

Use the transition matrix to identify the following probabilities concerning the state of the machine one hour from now
1. Find the probability that the machine is working on a job one hour from now if the machine is idle now.
2. Find the probability that the machine is idle one hour from now if the machine is working on a job now.
3. Find the probability that the machine is working on a job one hour from now if the machine is being repaired now.
4. Find the probability that the machine is being repaired in one hour if it is broken now.

Perform the appropriate calculations using the transition matrix to find the following probabilities concerning the state of the machine three hours from now.
1. Find the probability that the machine is working on a job three hours from now if the machine is idle now.
2. Find the probability that the machine is idle three hours from now if the machine is working on a job now.
3. Find the probability that the machine is working on a job three hours from now if the machine is being repaired now.
4. Find the probability that the machine is being repaired in three hours if it is broken now.

Questions 3-4 refer to the following description of how a Markov chain might be used to “train” a computer to generate music.

Teaching a computer music theory so that it can create music would be an extremely tedious task.
You would have to teach chord structure, different musical styles, and so on. What if you could give the program examples of pieces you considered to be music and ask it, “write something like that for me.” This is essentially how our Markov chain would work. The principle behind Markov chains in music is to generate a probability table to determine what note should come next. By feeding the program an example piece of music, the program can analyze the piece and create a probability table to determine which notes are more likely follow a given note. With the probability transition matrix one can generate random notes that still has some musical structure to it. By constructing a similar matrix for beats or note durations, one can complete a Markov chain model for music generation.

Source: © Dec 18, 2008 Frank Chen. Textbook content produced by Frank Chen is licensed under a Creative Commons Attribution License 2.0 license. Download for free at http://cnx.org/contents/62219fba-96df-418a-b9aa-14fddd7c30fa@2." Modified by Roberta Bloom, as permitted under this license.

The transition matrix below provides an example. The states are the notes A, A#,B,C,D,E,F,G,G#.
The matrix shows the probability of the next note (column state), given the current note (row state).

To generate computer created music, a computer program would randomly select the next note based on the previous note and the probabilities given in the transition matrix.

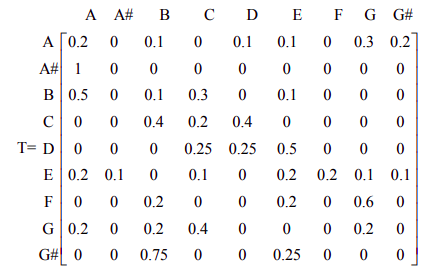
$Section10.5.2-3.png$

Find the probability for the next note, given the current note
1. P(next note is A | current note is G) = ______
2. P(next note is G | current note is A) = ______
3. P(next note is C | current note is F) = ______
4. P(next note is E | current note is D) = ______

4a. If the current note is A# (A-sharp) what does the transition matrix tell us about the next note?

4b. If the next note is F, what do we know about the current note.

Question 5 refers to the following:

Markov chains play an important role in online search.

“PageRank is an algorithm used by Google Search to rank websites in their search engine results. PageRank was named after Larry Page, one of the founders of Google. PageRank is a way of measuring the importance of website pages”
Source: https://en.Wikipedia.org/wiki/PageRank under the Creative Commons Attribution-ShareAlike License;

The theory behind PageRank is that pages that are linked to more often are more important and useful; identifying those that are linked to more often about a topic helps identify the pages that should be presented as most pertinent in a search.

In real world search, there are thousands or millions of pages linking together, resulting in huge transition matrices. Because of the size and other properties of these matrices, the mathematics behind PageRank is more sophisticated than the small example we examine here with only four websites. However our example is adequate to convey the main concept of PageRank and its use in search algorithms.

It should be noted that real world search algorithms, PageRank or similar Markov chain ranking schemes are only one of a variety of methods used.

Suppose we have 4 webpages that contains links to each other. We call the pages A, B, C, D.

From page A, 30% of people link to page B, 50% link to page C, and 20% link to page D
From page B, 50% of popele link to page A and 50% link to page D
From page C, 10% of people link to page B, 70% link to page C, and 20% link to page D
From page D, 20% of people link to page A, 40% to page B, 10% to page C, and 30% link to page D

(In this example, when a page links to itself, it means that a person viewing the page stays at that page and does not link to another page.)

Write the transition matrix T	Find the probability that a person viewing page C will link to page D next.
Find the probability that a person viewing page C will view page D after two links	Find the probability that a person viewing page C will view page D after three links
Find the probability that a person viewing page C will stay at page C and not link to any other page next.	Find the probability that a person viewing page C will view page A next