10.3.1: Regular Markov Chains (Exercises)

Last updated
Save as PDF

Page ID: 37936

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

SECTION 10.3 PROBLEM SET: REGULAR MARKOV CHAINS

Determine whether the following matrices are regular Markov chains.

$\left[\begin{array}{ll} 1 & 0 \\ .5 & .5 \end{array}\right]$	$\left[\begin{array}{rr} .6 & .4 \\ 0 & 1 \end{array}\right]$
$\left[\begin{array}{ccc} .6 & 0 & .4 \\ .2 & .4 & .4 \\ 0 & 0 & 0 \end{array}\right]$	$\left[\begin{array}{rrr} .2 & .4 & .4 \\ .6 & .4 & 0 \\ .3 & .2 & .5 \end{array}\right]$

Company I and Company II compete against each other, and the transition matrix for people switching from Company I to Company II is given below.

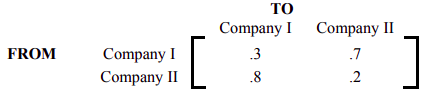
$Section10.5.3-2.png$

If the initial market share is 40% for Company I and 60% for Company II, what will the market share be after 3 transitions?

If this trend continues, what is the long range expectation for the market?

Suppose the transition matrix for a tennis player is as follows, where C denotes the cross-court shots and D denotes down-the-line shots.

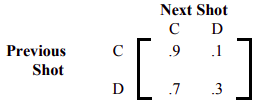
$Section10.5.3-3.png$

If the player hit the first shot cross-court, what is the probability he will hit the fourth shot cross-court?

Determine the long term shot distribution.

Professor Hay never orders eggs two days in a row, but if he orders tofu one day, then there is an equal probability that he will order tofu or eggs the next day.

Find the following:

If Professor Hay had eggs on Monday, what is the probability that he will have tofu on Friday?

Find the long term distribution for breakfast choices for Professor Hay.

In a bikeshare program with 3 bike stations, A, B, and C, people can borrow a bicycle at one station and return it to the same station or either of the other two stations. The transition matrix is:

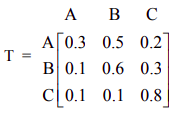
$Section10.5.3-5.png$

Find the following:

If a bicycle is initially at station A, what is the probability it will be at station C after 5 days?	If the initial distribution of bicycles is 50% at station A, 20% at station B, and 30% at station C, what will be the distribution after 2 days? After 5 days?
What will be the eventual long term distribution of bicycles at the stations?	If initially the distribution of bicycles at the stations was evenly distributed with one third of the bicycles at each station, will the eventual long term distribution be different than if the initial distribution is as given in part (c)?

Suppose that a country has 3 political parties: the Conservative (C), Liberal (L), and National (N) parties. If a person votes for the candidate from one party in an election, that person may decide to vote for the same party in the next election or may switch to vote for a candidate from another party in the next election. The transition matrix is:

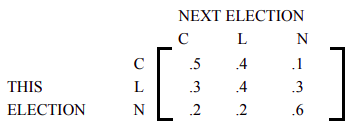
$Section10.5.3-6.png$

Assume there is an election every year, so the transition time is one year. Find the following.

If a person voted for the Liberal party in this election, find the probability that the person votes for the National party in the next election.	If a person voted for the National party in this election, find the probability that the person votes for the Conservative party in the election two years from now.
If in this election Conservatives received 25% of the votes, Liberals 30% of the votes, and Nationals the remaining 45% of the votes, what is the predicted distribution for the next election?	Assuming the current distribution from part (c), what will the distribution be in the election two years from now?
Assuming the current distribution from part (c), what will the distribution be in the election three years from now?	Determine the long term distribution.

Question 7 refers to the following:

Markov chains play an important role in online search.

“PageRank is an algorithm used by Google Search to rank websites in their search engine results. PageRank was named after Larry Page, one of the founders of Google. PageRank is a way of measuring the importance of website pages”
Source: https://en.Wikipedia.org/wiki/PageRank under the Creative Commons Attribution-ShareAlike License;

The theory behind PageRank is that pages that are linked to more often are more important and useful; identifying those that are linked to more often about a topic helps identify the pages that should be presented as most pertinent in a search.

In real world search, there are thousands or millions of pages linking together, resulting in huge transition matrices. Because of the size and other properties of these matrices, the mathematics behind PageRank is more sophisticated than the small example we examine here with only four websites. However our example is adequate to convey the main concept of PageRank and its use in search algorithms.

It should be noted that real world search algorithms, PageRank or similar Markov chain ranking schemes are only one of a variety of methodsused.

Suppose we have 4 webpages that contains links to each other. We call the pages A, B, C, D.

From page A, 30% of people link to page B, 50% link to page C, and 20% link to page D
From page B, 50% of popele link to page A and 50% link to page D
From page C, 10% of people link to page B, 70% link to page C, and 20% link to page D
From page D, 20% of people link to page A, 40% to page B, 10% to page C, and 30% link to page D

(In this example, when a page links to itself, it means that a person viewing the page stays at that page and does not link to another page.)

Write the transition matrix.	T is a $4 \times 4$ matrix, $n= 4$ states. Use the formula $m = ( n-1)^2 + 1$ to find the highest power $m$ that we need to check to determine if T is a regular Markov chain.
Is this a regular Markov chain? Explain how you determined that.	Find the equilibrium vector and write a sentence summarizing the long term distribution of visits to these sites based on this model.
In the equilibrium vector, the state with the highest probability has the highest “Page-rank” and as the probabilities decrease, the ranking decreases. Indicate the order of the ranking, from highest Page rank to lowest Page rank, of these 4 pages.

\(\left[\begin{array}{ll} 1 & 0 \\ .5 & .5 \end{array}\right]\)	\(\left[\begin{array}{rr} .6 & .4 \\ 0 & 1 \end{array}\right]\)
\(\left[\begin{array}{ccc} .6 & 0 & .4 \\ .2 & .4 & .4 \\ 0 & 0 & 0 \end{array}\right]\)	\(\left[\begin{array}{rrr} .2 & .4 & .4 \\ .6 & .4 & 0 \\ .3 & .2 & .5 \end{array}\right]\)

Write the transition matrix.	T is a \(4 \times 4\) matrix, \(n= 4\) states. Use the formula \(m = ( n-1)^2 + 1\) to find the highest power \(m\) that we need to check to determine if T is a regular Markov chain.
Is this a regular Markov chain? Explain how you determined that.	Find the equilibrium vector and write a sentence summarizing the long term distribution of visits to these sites based on this model.
In the equilibrium vector, the state with the highest probability has the highest “Page-rank” and as the probabilities decrease, the ranking decreases. Indicate the order of the ranking, from highest Page rank to lowest Page rank, of these 4 pages.