10.4.1: Absorbing Markov Chains (Exercises)

Last updated
Save as PDF

Page ID: 37937

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

SECTION 10.4 PROBLEM SET: ABSORBING MARKOV CHAINS

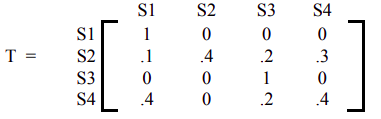
Given the following absorbing Markov chain.

$Section10.5.4-1.png$

Identify the absorbing states.	Write the solution matrix.
Starting from state 4, what is the probability of eventual absorption in state 1?	Starting from state 2, what is the probability of eventual absorption in state 3?

Two tennis players, Andre and Vijay each with two dollars in their pocket, decide to bet each other $1, for every game they play. They continue playing until one of them is broke.

Write the transition matrix for Andre.	Identify the absorbing states.
Write the solution matrix.	At a given stage if Andre has $1, what is the chance that he will eventually lose it all?

Repeat the previous problem, if the chance of winning for Andre is .4 and for Vijay .6.

Write the transition matrix for Andre.	Identify the absorbing states.
If Andre has $3, what is the probability that he will eventually be ruined?	If Vijay has $1, what is the probability that he will eventually triumph?

Repeat problem 2, if initially Andre has $3 and Vijay has $2.

Write the transition matrix.	Identify the absorbing states.
Write the solution matrix	If Andre has $4, what is the probability that he will eventually be ruined?

The non-tenured professors at a community college are regularly evaluated. After an evaluation they are classified as good, bad, or improvable. The "improvable" are given a set of recommendations and are re-evaluated the following semester. At the next evaluation, 60% of the improvable turn out to be good, 20% bad, and 20% improvable. These percentages never change and the process continues.

Write the transition matrix.	Identify the absorbing states.
Write the solution matrix	What is the probability that a professor who is improvable will eventually become good?

Questions 6 - 11 refer to the following:
In a professional certification program students take classes and then participate in an internships.
There are 4 states: taking classes (C), internship (I), drop out (D), and graduate (G).
If a student drops out they are never readmitted to the program.

Of those students currently taking classes, 70% have an internship the next year, 20% are still taking classes the next year, and 10% have dropped out by the next year. Of the students who are currently doing an internship, 65% graduate by the next year; 20% drop out by the next year, and 15% are still completing their internship the next year.

Write the transition matrix and indicate which are the absorbing states.	If a student is taking classes now: find the probability that the student will graduate in 2 years find the probability that the student will be in the internship in 2 years. find the probability that the student will have dropped out by 2 years from now.
Find the probability that a student currently doing an internship will eventually drop out.	Find the probability that a student taking classes now will eventually graduate.
If 40% of students are currently taking classes and 60% of current students are doing internships, what is the eventual long term distribution of students for graduating versus dropping out?	If 70% of students are currently taking classes and 30% of current students are doing internships, what is the eventual long term distribution of students for graduating versus dropping out?

A mouse is placed in the maze shown below, and it moves from room to room randomly. From any room, the mouse will choose a door to the next room with equal probabilities. Once the mouse reaches room 1, it finds food and never leaves that room. And when it reaches room 5, it is trapped and cannot leave that room. What is the probability the mouse will end up in room 5 if it was initially placed in room 3?

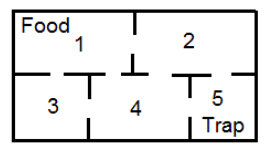
$Section10.5.4-12.png$

In problem 12, what is the probability the mouse will end up in room 1 if initially placed in room 2?