4.6: Multiplying Fractions
- Page ID
- 9847
Area Model
One of our models for multiplying whole numbers was an area model. For example, the product \(23 \times 37\) is the area (number of 1 × 1 squares) of a 23-by-37 rectangle:

So the product of two fractions, say, \(\frac{4}{7} \times \frac{2}{3}\) should also correspond to an area problem.
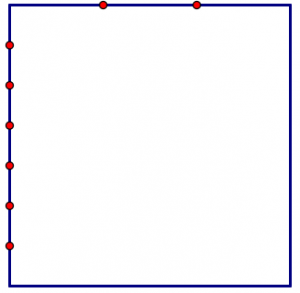
Let us start with a segment of some length that we call 1 unit:

Now, build a square that has one unit on each side:

The area of the square, of course, is \(1 \times 1 = 1\) square unit.
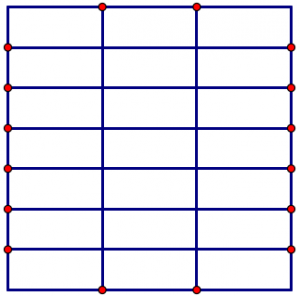
Now, let us divide the segment on top into three equal-sized pieces. (So each piece is \(\frac{1}{3}\).) And we will divide the segment on the side into seven equal-sized pieces. (So each piece is \(\frac{1}{7}\).)
We can use those marks to divide the whole square into small, equal-sized rectangles. (Each rectangle has one side that measures \(\frac{1}{3}\) and another side that measures \(\frac{1}{7}\).)
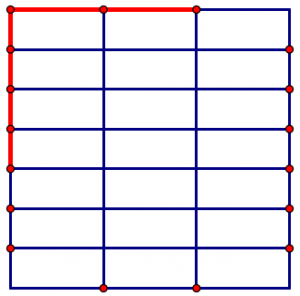
We can now mark off four sevenths on one side and two thirds on the other side.
The result of the multiplication should be the area of the rectangle with \(\frac{4}{7}\) on one side and \(\frac{2}{3}\) on the other. What is that area?
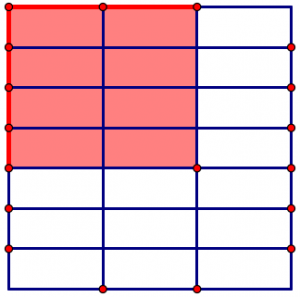
Remember, the whole square was one unit. That one-unit square is divided into 21 equal-sized pieces, and our rectangle (the one with sides \(\frac{4}{7}\) and \(\frac{2}{3}\)) contains eight of those rectangles. Since the shaded area is the answer to our multiplication problem we conclude that
\[\frac{4}{7} \times \frac{2}{3} = \frac{8}{21} \ldotp \nonumber \]
- Use are model to compute each of the following products. Draw the picture to see the answer clearly. $$\frac{3}{4} \times \frac{5}{6}, \qquad \frac{3}{8} \times \frac{4}{5}, \qquad \frac{5}{8} \times \frac{3}{7} \ldotp$$
- The area problem \(\frac{4}{7} \times \frac{2}{3}\) yielded a diagram with a total of 21 small rectangles. Explain why 21 appears as the total number of equal-sized rectangles.
- The area problem \(\frac{4}{7} \times \frac{2}{3}\) yielded a diagram with 8 small shaded rectangles. Explain why 8 appears as the number of shaded rectangles.
How can you extend the area model for fractions greater than 1? Try to draw a picture for each of these: \[\frac{3}{4} \cdot \frac{3}{2}, \qquad \frac{2}{5} \cdot \frac{4}{3}, \qquad \frac{3}{10} \cdot \frac{5}{4}, \qquad \frac{5}{2} \cdot \frac{7}{4} \ldotp \nonumber \]
On Your Own
Work on the following exercises on your own or with a partner.
- Compute the following products, simplifying each of the answers as much as possible. You do not need to draw pictures, but you may certainly choose to do so if it helps! $$\frac{5}{11} \times \frac{7}{12}, \qquad \frac{4}{7} \times \frac{4}{8}, \qquad \frac{1}{2} \times \frac{1}{3}, \qquad \frac{2}{1} \times \frac{3}{1}, \qquad \frac{1}{5} \times \frac{5}{1}\ldotp$$
- Compute the following products. (Do not work too hard!) $$\frac{3}{4} \times \frac{1}{3} \times \frac{2}{5}, \qquad \frac{5}{5} \times \frac{7}{8}, \qquad \frac{88}{88} \times \frac{541}{788}, \qquad \frac{77876}{311} \times \frac{311}{77876} \ldotp$$
- Try this one. Can you make use of the fraction rule \(\frac{xa}{xb} = \frac{a}{b}\) to help you calculate? How? $$\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} \times \frac{4}{5} \times \frac{5}{6} \times \frac{6}{7} \times \frac{7}{8} \times \frac{8}{9} \times \frac{9}{10} \ldotp$$
How are these two problems different? Draw a picture of each.
- Pam had \(\frac{2}{3}\) of a cake in her refrigerator, and she ate \(\frac{1}{2}\) of it. How much total cake did she eat?
- On Monday, Pam ate \(\frac{2}{3}\) of a cake. On Tuesday, Pam ate \(\frac{1}{2}\) of a cake. Both cakes were the same size. How much total cake did she eat?
When a problem includes a phrase like “\(\frac{2}{3}\) of …,” students are taught to treat “of” as multiplication, and to use that to solve the problem. As the above problems show, in some cases this makes sense, and in some cases it does not. It is important to read carefully and understand what a problem is asking, not memorize rules about “translating” word problems.
Explaining the Rule
You probably simplified your work in the exercises above by using a multiplication rule like the following.
\[\frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \ldotp \nonumber \]
Of course, you may then choose to simplify the final answer, but the answer is always equivalent to this one. Why? The area model can help us explain what is going on.
First, let us clearly write out how the area model says to multiply \(\frac{a}{b} \cdot \frac{c}{d}\). We want to build a rectangle where one side has length \(\frac{a}{b}\) and the other side has length \(\frac{c}{d}\). We start with a square, one unit on each side.
- Divide the top segment into
equal-sized pieces. Shade
of those pieces. (This will be the side of the rectangle with length \(\frac{a}{b}\).)
- Divide the left segment into
equal-sized pieces. Shade
of those pieces. (This will be the side of the rectangle with length \(\frac{c}{d}\).)
- Divide the whole rectangle according to the tick marks on the sides, making equal-sized rectangles.
- Shade the rectangle bounded by the shaded segments.
If the answer is \(\frac{a \cdot c}{b \cdot d}\), that means there are \(b \cdot d\) total equal-sized pieces in the square, and \(a \cdot c\) of them are shaded. We can see from the model why this is the case:
- The top segment was divided into
equal-sized pieces. So there are
columns in the rectangle.
- The side segment was divided into
equal-sized pieces. So there are
rows in the rectangle.
- A rectangle with
columns and
rows has \(b \cdot d\) pieces. (The area model for whole-number multiplication!)
Stick with the general multiplication rule
\[\frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \ldotp \nonumber \]
Write a clear explanation for why \(a \cdot c\) of the small rectangles will be shaded.
Multiplying Fractions by Whole Numbers
Often, elementary students are taught to multiply fractions by whole numbers using the fraction rule.
For example, to multiply \(2 \cdot \frac{3}{7}\), we think of “2” as \(\frac{2}{1}\), and compute this way \[2 \cdot \frac{3}{7} = \frac{2}{1} \cdot \frac{3}{7} = \frac{2 \cdot 3}{1 \cdot 7} = \frac{6}{7} \ldotp \nonumber \]
We can also think in terms of our original “Pies Per Child” model to answer questions like this.
We know that \(\frac{3}{7}\) means the amount of pie each child gets when 7 children evenly share 3 pies.
If we compute \(2 \cdot \frac{3}{7}\) that means we double the amount of pie each kid gets. We can do this by doubling the number of pies. So the answer is the same as \(\frac{6}{7}\): the amount of pie each child gets when 7 children evenly share 6 pies.
Finally, we can think in terms of units and unitizing.
The fraction \(\frac{3}{7}\) means that I have 7 equal pieces (of something), and I take 3 of them.
So \(2 \cdot \frac{3}{7}\) means do that twice. If I take 3 pieces and then 3 pieces again, I get a total of 6 pieces. There are still 7 equal pieces in the whole, so the answer is \(\frac{6}{7}\).
- Use all three methods to explain how to find each product: $$3 \cdot \frac{2}{5}, \qquad 4 \cdot \frac{3}{8}, \qquad 6 \cdot \frac{1}{5} \ldotp$$
- Compare these different ways of thinking about fraction multiplication. Are any of them more natural to you? Does one make more sense than the others? Do the particular numbers in the problem affect your answer? Does your partner agree?
Explaining the Key Fraction Rule
Roy says that the fraction rule
\[\frac{xa}{xb} = \frac{a}{b} \nonumber \]
is “obvious” if you think in terms of multiplying fractions. He reasons as follows:
We know multiplying anything by 1 does not change a number:
\[\begin{split} 1 \cdot 4 &= 4 \\ 1 \cdot 2014 &= 2014 \\ 1 \cdot \frac{5}{7} &= \frac{5}{7} \end{split} \nonumber \]
So, in general,
\[1 \cdot \frac{a}{b} = \frac{a}{b} \ldotp \nonumber \]
Now, \(\frac{2}{2} = 1\), so that means that
\[\frac{2}{2} \cdot \frac{a}{b} = 1 \cdot \frac{a}{b} = \frac{a}{b}, \nonumber \]
which means
\[\frac{2a}{2b} = \frac{a}{b} \ldotp \nonumber \]
By the same reasoning, \(\frac{3}{3} = 1\), so that means that
\[\frac{3}{3} \cdot \frac{a}{b} = 1 \cdot \frac{a}{b} = \frac{a}{b}, \nonumber \]
which means
\[\frac{3a}{3b} = \frac{a}{b} \ldotp \nonumber \]
What do you think about Roy’s reasoning? Does it make sense? How would Roy explain the general rule for positive whole numbers :
\[\frac{xa}{xb} = \frac{a}{b} ? \nonumber \]


