7.4: Polygons
- Page ID
- 9866
It can seem like the study of geometry in elementary school is nothing more than learning a bunch of definitions and then classifying objects. In this part, you’ll explore some problem solving and reasoning activities that are based in geometry. But definitions are still important! So let’s start with this one.
A polygon is:
- a plane figure
- that is bounded by a finite number of straight line segments
- in which each segment meets exactly two others, one at each of its endpoints.
Just as the first step in problem solving is to understand the problem, the first step in reading a mathematical definition is to understand the definition.
- Use the definition above to draw several examples of figures that are definitely polygons. (You should be able to say why your example fits the definition.)
- Draw several non-examples as well: shapes that are definitely not polygons. (You should be able to say which part of the definition fails for your non-examples.)
A few comments about polygons:
- The line segments that make up a polygon are called its edges and the points where they meet are called its vertices (singular: vertex).
- Because of properties (2) and (3) in the definition, the boundaries of polygons are not self-intersecting.
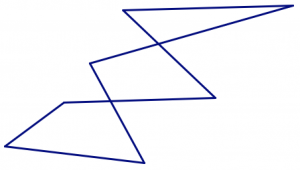
Not a polygon.
- Polygons are named based on the number of sides they have.
| name | # of sides | examples |
|---|---|---|
| triangle | 3 |  |
| quadrilateral | 4 | 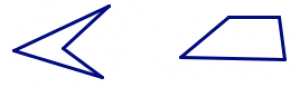 |
| pentagon | 5 | 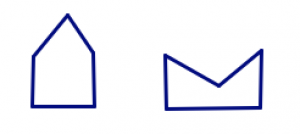 |
| hexagon | 6 | 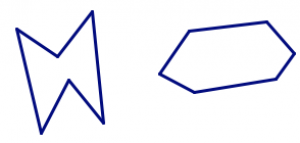 |
| heptagon | 7 | |
| octagon | 8 | |
| nonagon | 9 | |
| decagon | 10 |
- In general, we call a polygon with n sides an n-gon.
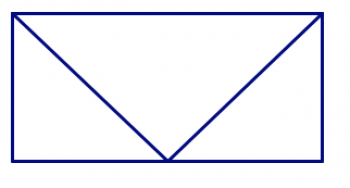
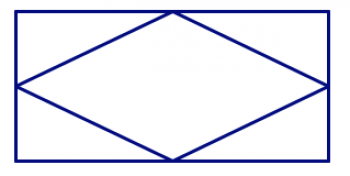
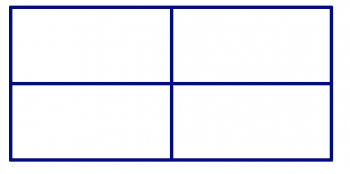
In the pictures below, there are polygons hidden in the design. In each design, find all of the triangles, quadrilaterals, pentagons, and hexagons. How can you be sure you’ve found them all and haven’t counted any twice?

Angle Sum
You know that the sum of the interior angles in any triangle is 180°. Can you say anything about the angles in other polygons?
You probably know that rectangles have four 90° angles. So if if all quadrilaterals have the same interior angle sum, it must be 360° (since 4 × 90° = 360°).
But notice: We don’t necessarily have any reason to believe this constant sum would be true. Remember that SSS congruence is true for triangles, but not for any other polygons. Triangles are special, and we shouldn’t assume that true statements about triangles will hold true for other shapes.
Any quadrilateral can be split into two triangles, where the vertices of the triangles all coincide with the vertices of the quadrilateral:

Use the pictures above to carefully explain why all quadrilaterals do, indeed, have an angle sum of 360°.
On Your Own
Work on the following exercises on your own or with a partner.
- Draw several different pentagons on your paper. Show that each of them can be split into exactly three triangles in such a way that the vertices of the triangles all coincide with the vertices of the pentagon.
- Use the fact that every pentagon can be split into three triangles in this way to find the sum of the angles in any pentagon.
- Draw several different hexagons on your paper. Show that each of them can be split into exactly four triangles so that the vertices of the triangles all coincide with the vertices of the hexagon.
- Use the fact that every hexagon can be split into four triangles in this way to find the sum of the angles in any hexagon.
Use your work on the exercises above to complete this general statement:
Angle Sum in Polygons
The sum of the interior angles in an n-gon (a polygon with n sides) is
__________________________.
Explain how you know your statement is true.
A regular polygon has all sides the same length and all angles the same measure.
For example, squares are regular quadrilaterals — all four sides are the same length, and all four angles measure 90°. But a non-square rectangle is not regular. Even though all of the angles are 90°, the sides are not all the same length. Similarly, a non-square rhombus is not regular. Even though the sides of a rhombus are all the same length, the angles can be different.

Since a square is a regular quadrilateral, you know that every angle in a regular quadrilateral measure 90°. What about angles in other regular polygons?
- What is the measure of each angle in a regular triangle? Explain how you know you are right.
- What is the measure of each angle in a regular pentagon? Explain how you know you are right.
- What is the measure of each angle in a regular hexagon? Explain how you know you are right.
- What is the measure of each angle in a regular n-gon? Explain how you know you are right.


