7.5: Platonic Solids

Last updated
Save as PDF

Page ID: 9867

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Of course, we live in a three-dimensional world (at least!), so only studying flat geometry doesn’t make a lot of sense. Why not think about some three-dimensional objects as well?

Definition

A polyhedron is a solid (3-dimensional) figure bounded by polygons. A polyhedron has faces that are flat polygons, straight edges where the faces meet in pairs, and vertices where three or more edges meet.

The plural of polyhedron is polyhedra.

Think / Pair / Share

Look at the pictures of solids below, and decide which are polyhedra and which are not. You should be able to say why each figure does or does not fit the definition.

^[1]
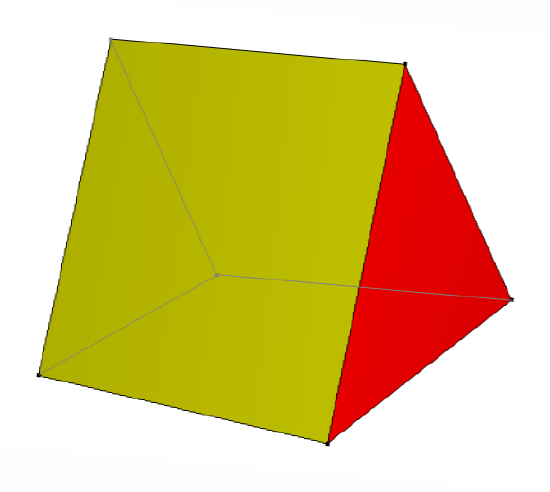
$Triangular_prism_wedge.png$
^[2]
$cylinder-225x243.png$
^[3]
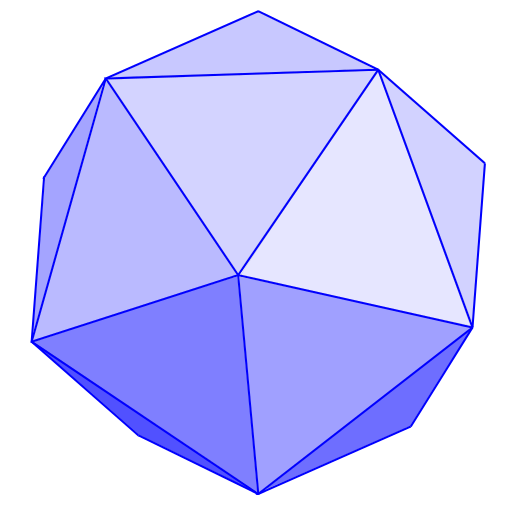
$512px-Euclid_Icosahedron_3.svg_.png$
^[4]
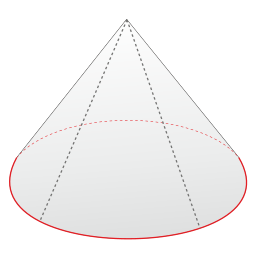
$256px-Circular_cone.svg_.png$
^[5]
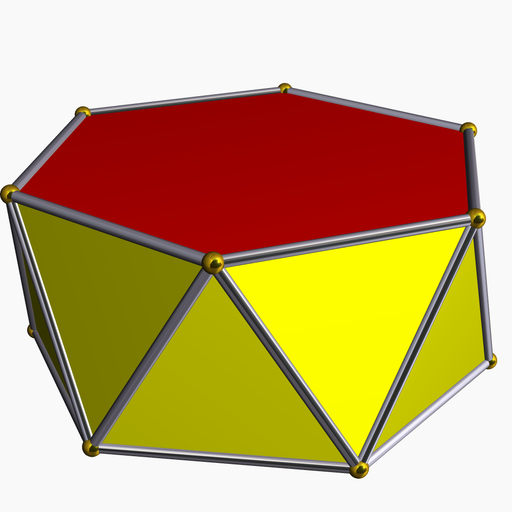
$512px-Hexagonal_antiprism.png$
^[6]
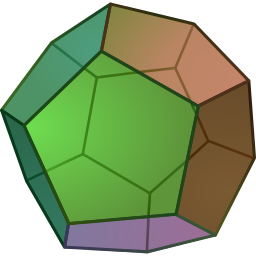
$256px-Dodecahedron.svg_.png$
^[7]
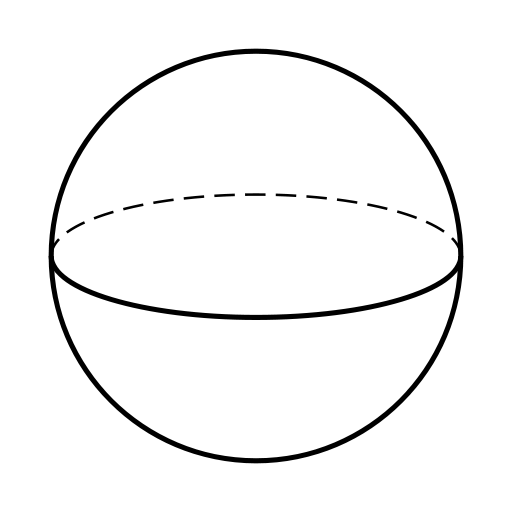
$512px-Sphere.svg_.png$
^[8]
$512px-Torus_illustration.png$
^[9]
$128px-Stella_octangula.svg_.png$

Remember that a regular polygon has all sides the same length and all angles the same measure. There is a similar (if slightly more complicated) notion of regular for solid figures.

Definition

A regular polyhedron has faces that are all identical (congruent) regular polygons. All vertices are also identical (the same number of faces meet at each vertex).

Regular polyhedra are also called Platonic solids (named for Plato).

If you fix the number of sides and their length, there is one and only one regular polygon with that number of sides. That is, every regular quadrilateral is a square, but there can be different sized squares. Every regular octagon looks like a stop sign, but it may be scaled up or down. Your job in this section is to figure out what we can say about regular polyhedra.

On Your Own

Work on the following exercises on your own or with a partner. You will need to make lots of copies of the regular polygons below. Copy and cut out at least:

40 copies of the equilateral triangle,
15 copies of the square,
20 copies of the regular pentagon, and
10 copies each of the hexagon, heptagon, and octagon.

You will also need some tape.

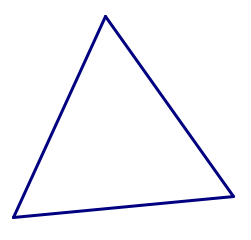
$eqtri.png$

$square3.png$

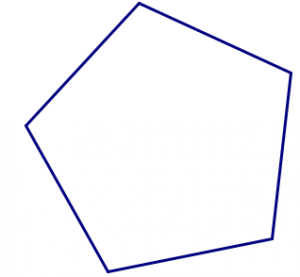
$pentagon-300x277.png$

$hexagon-300x255.png$

$heptagon-300x287.png$

$octagon-300x293.png$

In any polyhedron, at least three polygons meet at each vertex. Start with the equilateral triangles: Put three of them together meeting at a vertex and tape them together. Then close them up so they form a solid shape. Can you complete this shape into a platonic solid? Be sure to check that at every vertex you have exactly three triangles meeting.
Now repeat this process, but start with four equilateral triangles around a single vertex. Then close them up so they form a solid shape. Can you complete this into a platonic solid? Be sure to check that at every vertex you have exactly four triangles meeting.
Repeat this process with five equilateral triangles, then six, then seven, and so on. Keep going until you are convinced you understand what’s happening with Platonic solids that have triangular faces.
When you are done with triangular faces, move on to square faces. Work systematically: Try to build a Platonic solid with three squares at each vertex, then four, then five, etc. Keep going until you can make a definitive statement about Platonic solids with square faces.
Repeat this process with the other regular polygons you cut out: pentagons, hexagons, heptagons, and octagons.

You must have noticed that the situation for Platonic solids is quite different from the situation for regular polygons. There are infinitely many regular polygons (even if you don’t account for size). There is a regular polygon with n sides for every value of n bigger than 2. But for solids, we have the following (perhaps surprising) result.

Theorem

There are exactly five Platonic solids.

The key fact is that for a three-dimensional solid to close up and form a polyhedron, there must be less than 360° around each vertex. Otherwise, it either lies flat (if there is exactly 360°) or folds over on itself (if there is more than 360°).

Problem 9

Based on your work in the exercises, you should be able to write a convincing justification of the Theorem above. Here’s a sketch, and you should fill in the explanations.

If a Platonic solid has faces that are equilateral triangles, then fewer than 6 faces must meet at each vertex. Why?
If a Platonic solid has square faces, then three faces can meet at each vertex, but not more than that. Why?
If a Platonic solid has faces that are regular pentagons, then three faces can meet at each vertex, but not more than that. Why?
Regular hexagons cannot be used as the faces for a Platonic solid. Why?
Similarly, regular n-gons for n bigger than 6 cannot be used as the faces for a Platonic solid. Why?

Image by Tom Ruen [Public domain], via Wikimedia Commons ↵
Image via pixababy.com, CC0 Creative Commons license. ↵
Image by Aldoaldoz (Own work) [CC BY-SA 3.0, via Wikimedia Commons. ↵
Image by By Thinkingarena (Own work) [CC BY-SA 4.0], via Wikimedia Commons ↵
Image by Robert Webb's Stella software: http://www.software3d.com/Stella.php, via Wikimedia Commons. ↵
Image DTR CC-BY-SA-3.0], via Wikimedia Commons ↵
Imgae by Stephen.G.McAteer (Own work) [CC BY-SA 3.0], via Wikimedia Commons. ↵
Imgae via Wikimedia Commons [Public domain]. ↵
Image by self [CC BY-SA 3.0], via Wikimedia Commons. ↵

Search

Text Color

Text Size

Margin Size

Font Type

Theorem

Problem 9