7.7: Symmetry
- Page ID
- 13697
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Mathematicians use symmetry in all kinds of situations. There can be symmetry in calculations, for example. But the most recognizable kinds of symmetry are those in geometric designs.
Geometric and real-world objects can have different kinds of symmetries[1].

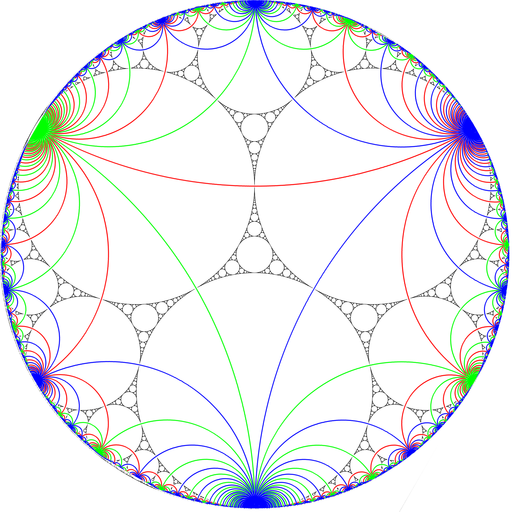


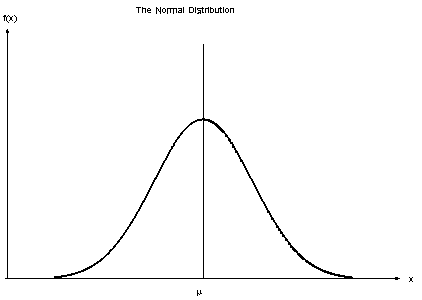

Or they might have no symmetry[2] at all.



- What do you already know about the idea of symmetry? What does it mean to say a design is symmetric?
- Do you know about different types of symmetry? What types?
- Can you give examples of real-world objects that are symmetric? What about objects that are not symmetric?
Line Symmetry
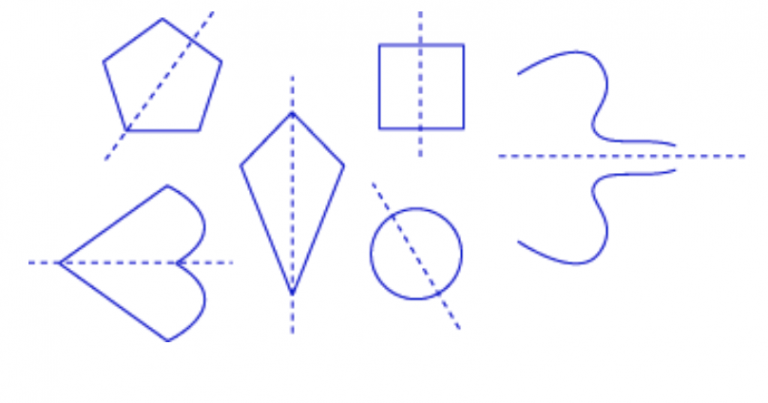
If you can flip a figure over a line — this is called reflecting the figure — and then it appears unchanged, then the figure has reflection symmetry or line symmetry. A line of symmetry divides an object into two mirror-image halves. The dashed lines below are lines of symmetry:
Compare with the dashed lines below. Though they do cut the figures in half, they don’t create mirror-image halves. These are not lines of symmetry:
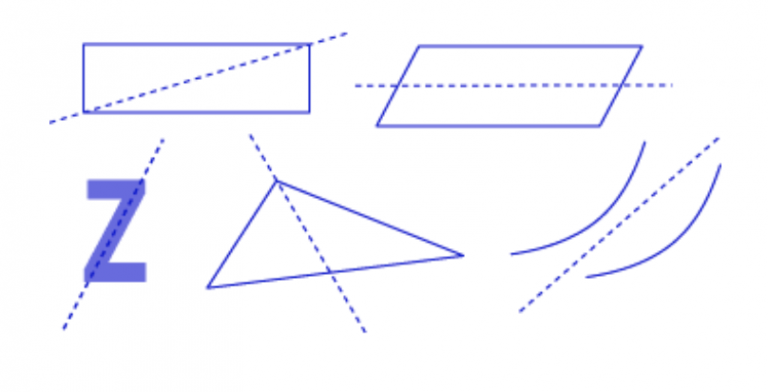
Look at the first set of pictures at the start of this chapter. Do any of them have lines of symmetry? How can you tell?
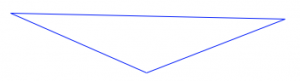
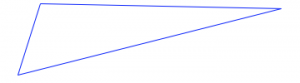
For each of the figures[3] below:
- Decide if it has any lines of symmetry. If not, how do you know?
- If it does have one or more lines of symmetry, find / describe all of them. Explain how you did it.




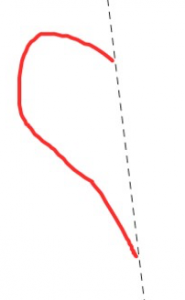
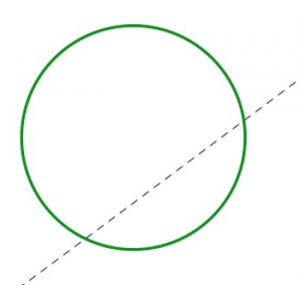
Each picture below shows half of a design with line symmetry. The line of symmetry (dashed) is shown. Can you complete the design? Explain how you did it.
Rotational Symmetry
If you can turn a figure around a center point less than a full circle — this is called a rotation — and the figure appears unchanged, then the figure has rotational symmetry. The point around which you rotate is called the center of rotation, and the smallest angle you need to turn is called the angle of rotation.
This star has rotational symmetry of 72°, and the center of rotation is the center of the star. One point is marked to help you visualize the rotation.
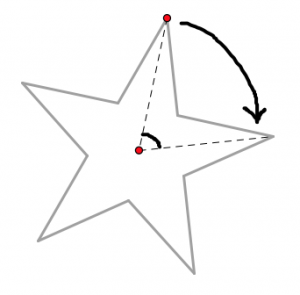

- How can you be certain that the angle of rotation for the star is exactly 72°?
- Look at the first set of pictures at the start of this chapter. Do any of them have rotational symmetry? How can you tell?
Each of the figures below has rotational symmetry. Find the center of rotation and the angle of rotation. Explain your thinking.


Each picture below shows part of a design with a marked center of rotation and an angle of rotation given. Can you complete the design so that it has the correct rotational symmetry? Explain how you did it.
90° 45°
Translational Symmetry
A translation (also called a slide) involves moving a figure in a specific direction for a specific distance. A vector (a line segment with an arrow on one end) can be used to describe a translation, because the vector communicates both a distance (the length of the segment) and a direction (the direction the arrow points).

A design has translational symmetry if you can perform a translation on it and the figure appears unchanged. A brick wall[4] has translational symmetry in lots of directions!

The brick wall is one example of a tessellation[5], which you’ll learn more about in the next chapter.



You can see translation symmetry in lots of places. It’s in architecture and design[6].



It’s in art, most famously that by M.C. Escher. (You might want to visit http://www.mcescher.com/gallery/symmetry/ and browse the “Symmetry” gallery.)
And it appears in traditional Hawaiian and other Polynesian tattoo[7]designs.



- On each of the pictures with translational symmetry above, sketch a vector to indicate the direction and distance of the translational symmetry.
- Create your own design with translational symmetry. Explain how you did it.
- Mosaic image by MarcCooperUK (Flickr: Paris central mosque) [CC BY 2.0], via Wikimedia Commons. Apollonian Circle Packing by Tomruen (Own work) [CC BY-SA 3.0], via Wikimedia Commons. Butterfly by Bernard DUPONT from FRANCE (Swallowtail Butterfly (Papilio oribazus)) [CC BY-SA 2.0], via Wikimedia Commons. Starfish by Paul Shaffner [CC BY 2.0], via Wikimedia Commons. Normal distribution from Wikimedia Commons [Public domain]. Water drop from pixababy.com [CC0 Creative Commons]. ↵
- Pillar coral, wave, and molecule from Wikimedia commons [Public domain]. Head of a woman by Pablo Picasso, image from Gandalf's Gallery on flickr [CC-BY-NC-SA 2.0] ↵
- Circle and ellipse by Paris 16 (Own work) [CC BY-SA 4.0], via Wikimedia Commons ↵
- Image by I, Xauxa [CC-BY-SA-3.0], via Wikimedia Commons ↵
- Triangular tessellation from pixababy [CC0]. Hexagonal and rhombic tessellations from Wikimedia Commons [Public domain]. ↵
- Tile at Jerusalem temple by Andrew Shiva / Wikipedia, via Wikimedia Commons [CC BY-SA 4.0]. Mosque by Hisham Binsuwaif via flickr [CC BY-SA 2.0]. British Museum great court by Andrew Dunn, http://www.andrewdunnphoto.com/ (Own work) [CC BY-SA 2.0], via Wikimedia Commons ↵
- Royal Hawaiian officer via Wikimedia Commons [Public domain]. Shoulder and arm tattoos by Micael Faccio on flicker [CC BY-2.0]. ↵


