7.9: Problem Bank
- Page ID
- 13723
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the Tangrams chapter, you first saw all 7 tangram pieces arranged into a square.
- If the large square you made with all seven pieces is one whole, assign a (fractional) value to each of the seven tangram pieces. Justify your answers.
- The tangram puzzle contains a small square. If the small square (the single tangram piece) is one whole, assign a value to each of the seven tangram pieces. Justify your answers.
- The tangram set contains two large triangles. If a large triangle (the single tangram piece) is one whole, assign a value to each of the seven tangram pieces. Justify your answers.
- The tangram set contains one medium triangle. If the medium triangle (the single tangram piece) is one whole, assign a value to each of the seven tangram pieces. Justify your answers.
- The tangram set contains two small triangles. If a small triangle (the single tangram piece) is one whole, assign a value to each of the seven tangram pieces. Justify your answers.
If possible sketch an example of the following triangles. If it is not possible, explain why not.
- A right triangle that is scalene.
- A right triangle that is isosceles.
- A right triangle that is equilateral.
If possible sketch an example of the following triangles. If it is not possible, explain why not.
- An acute triangle that is scalene.
- An acute triangle that is isosceles.
- An acute triangle that is equilateral.
If possible sketch an example of the following triangles. If it is not possible, explain why not.
- An obtuse triangle that is scalene.
- An obtuse triangle that is isosceles.
- An obtuse triangle that is equilateral.
If possible sketch an example of the following triangles. If it is not possible, explain why not.
- An equiangular triangle that is scalene.
- An equiangular triangle that is isosceles.
- An equiangular triangle that is equilateral.
Look at the picture below, which shows two lines intersecting. Angles A and D are called “vertical angles,” and so are angles B and C.
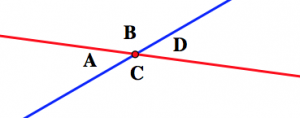
Use this drawing to explain why vertical angles must have the same measure. (Hint: what is the sum of the measures of angle A angle B? How do you know?)
Answer the following questions about the triangle below. Be sure to focus on what you know for sure and not what the picture looks like.
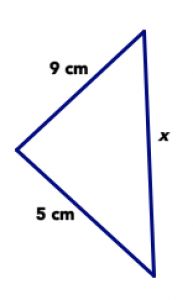
- Could it be true that x = 4 cm? Explain your answer.
- Could it be true that x = 20 cm? Explain your answer.
- Give three possible values of x, based on the information in the picture.
Answer the following questions about the triangle below. Be sure to focus on what you know for sure and not what the picture looks like.
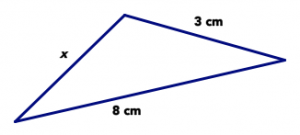
- If x = 3 cm, the triangle is isosceles. Is this possible? Explain your answer.
- If x = 8 cm, the triangle is isosceles. Is this possible? Explain your answer.
- Give three impossible values of x, based on the information in the picture.
Prof. Faber drew this picture on the board, saying it showed three triangles: △ABC, △ABD, and △CBD. Side lengths and angle measurements are shown for each of the triangles.
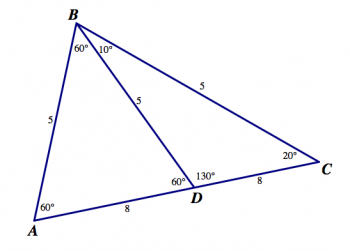
There are lots of mistakes in this picture. Use what you know about side lengths and angles in triangles to find all the mistakes you can. For each mistake, say what is wrong with the picture, and why it’s a mistake. Explain your thinking as clearly as you can.
Because of SSS congruence, triangles are exceptionally sturdy. This means they are used frequently in architecture and design to provide supports for buildings, bridges, and other man-made objects. Take your camera with you, and find several places in your neighborhood or near your campus that use triangular supports. Snap a picture, and describe what the structure is and where you see the triangles.
It is possible to create designs that have multiple symmetries. See if you can find images (or create your own!) that have both:
- reflection symmetry and rotational symmetry,
- reflection symmetry and translational symmetry, and
- rotational symmetry and translational symmetry.


