14.2: Calculating a Bond’s Yield
- Page ID
- 22153
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Should you always hold onto a bond until maturity? Is there a best time to sell? In the opener to the last section, you invested in 10 Government of Canada $5,000 face value bonds with a 5% coupon and 20 years remaining to maturity. For these you paid $4,699.02 each when prevailing bond rates were 5.5%. Ten years after you purchased those bonds, prevailing bond market rates have dropped to 3.35% but are expected to rise in the near future. Is now the time to sell those bonds?
This is a complex decision with many variables; however, to help make that decision you must know at least three critical pieces of information: the selling price of the bond, the yield you would realize on your investment if you held onto the bond until maturity, and the yield if you sold the bond today.
This section integrates the calculations of bond prices and bond yields so that you better understand your bond investments. These guidelines apply whether you are investing personally or on behalf of your company.
Yield to Maturity
The yield to maturity, also known as basis, is a bond's overall rate of return when purchased at a market price and held until maturity. It includes both the semi-annual interest that the bondholders earn on their investment along with the gain or loss resulting from the difference between the market price on the selling date and the redemption price. This yield to maturity is exactly equal to the market rate of return on the date of purchase. Thus, in the example above, if you hang on to those bonds until maturity, you will realize a yield to maturity of 5.5%.
In this section, you are turning around the calculations from Section 14.1, where you answered the question, "Knowing the market rate of return, what will you pay?" Now you are asked, "Knowing what you pay, what is the market rate of return?" Thus, rewording the opening example you would have: “If you paid $4,699.02 for a $5,000 face value bond with 20 years to maturity having a 5% coupon, what yield to maturity would you realize?"
The Formula
You need no new formulas to calculate a bond's yield to maturity. The goal is to solve for the nominal rate of interest, or \(IY\). You must work with Formulas 14.2, 14.3, and 9.1. Recall that Formula 14.2 determines the semi-annual bond coupon interest payment amount. You substitute this amount into Formula 14.3, which calculates the price of the bond on an interest payment date. However, in this case you must solve Formula 14.3 not for the date price but for the periodic rate of interest, or i. Once you know the periodic interest rate, you can substitute it into Formula 9.1 and solve for the nominal interest rate, or \(IY\).
One problem in using the formula approach is that it is impossible to algebraically isolate the periodic interest rate in Formula 14.3. You must turn to technology such as the BAII Plus calculator or Excel.
How It Works
Follow these steps to calculate a bond's yield to maturity:
Step 1: Draw a timeline like the one presented here, extending from the selling date to the maturity date. Identify all known variables.

Step 2: Using Formula 14.2, calculate the amount of the bond interest payment.
Step 3: As in Section 14.1, use Formula 11.1 to calculate the \(N\). Since the market rate and the coupon rate are both semi-annual, the \(N\) is used as both the total number of compounds and the total number of payments.
- If using a manual method, substitute all known numbers into Formula 14.3 and attempt to solve for the periodic interest rate (\(i\)). Once you know this, convert it to a nominal interest rate using Formula 9.1.
- Alternatively, if you are using technology such as the calculator, input all known variables and solve directly for the nominal interest rate (\(IY\)).
Important Notes
Note two conditions when you calculate yield to maturity:
- Trading takes place only on interest payment dates.
- The bondholder reinvests all coupon payments at the same rate of interest. Calculations not meeting these conditions are beyond the introductory scope of this textbook.
If you purchase a bond with a coupon rate of 4% when the market rate is 5%, what yield to maturity will you realize?
- Answer
-
5%; your yield to maturity depends on the market rate, not the coupon rate.
Suppose a $10,000 face value bond is purchased for $7,688.52 with 20 years until maturity and has a coupon rate of 4% semi-annually. What yield will the bondholder realize if she holds onto it until maturity?
Solution
The yield to maturity represents the nominal rate of interest on the bond, or \(IY\).
What You Already Know
Step 1:
The timeline for the bond sale appears below.
Coupon Interest Payment: \(CPN\) = 4%, \(CY\) = 2, Face Value = $10,000
Bond: Date Price = $7,688.52, \(FV\) = $10,000, \(CY\) = 2, \(PMT_{BOND}\) = Formula 14.2, \(PY\) = 2, Years Remaining = 20
How You Will Get There
Step 2:
Apply Formula 14.2 to determine the periodic bond interest payment.
Step 3:
Apply Formulas 11.1, 14.3, and 9.1 to determine the yield to maturity (\(IY\)). Solve Formulas 14.3 and 9.1 using the calculator.

Calculations
Step 2:
\[PMT_{BOND}=\$ 10,000 \times \dfrac{0.04}{2}=\$ 200 \nonumber \]
Step 3:
\(N=2 \times 20=40\) (compounds and payments)
\[\$ 7,688.52=\dfrac{\$ 10,000}{(1+i)^{40}}+\$ 200\left[\dfrac{1-\left[\dfrac{1}{1+i}\right]^{40}}{i}\right] \quad i=\dfrac{\mathrm{IY}}{2} \nonumber \]
Calculator output \(= IY = 6%\)
Calculator Instructions
| Mode | N | I/Y | PV |
|---|---|---|---|
| END | 40 | Answer: 6.000002 | -7688.52 |
| PMT | FV | P/Y | C/Y |
|---|---|---|---|
| 200 | 10,000 | 2 | 2 |
If she holds onto the bond for the next 20 years, she will realize a yield to maturity of 6% compounded semi-annually.
The Investor’s Yield
The yield-to-maturity calculation requires that the bond be held until its maturity date, at which point the future value redemption price is known and equal to its face value. However, this condition may not hold. The bondholder may sell the bond at any point before the maturity date. If the bond is sold, the future value is based on the prevailing bond rate at that time, and the price is generally not equal to its face value. What then is the bond’s yield for the investor?
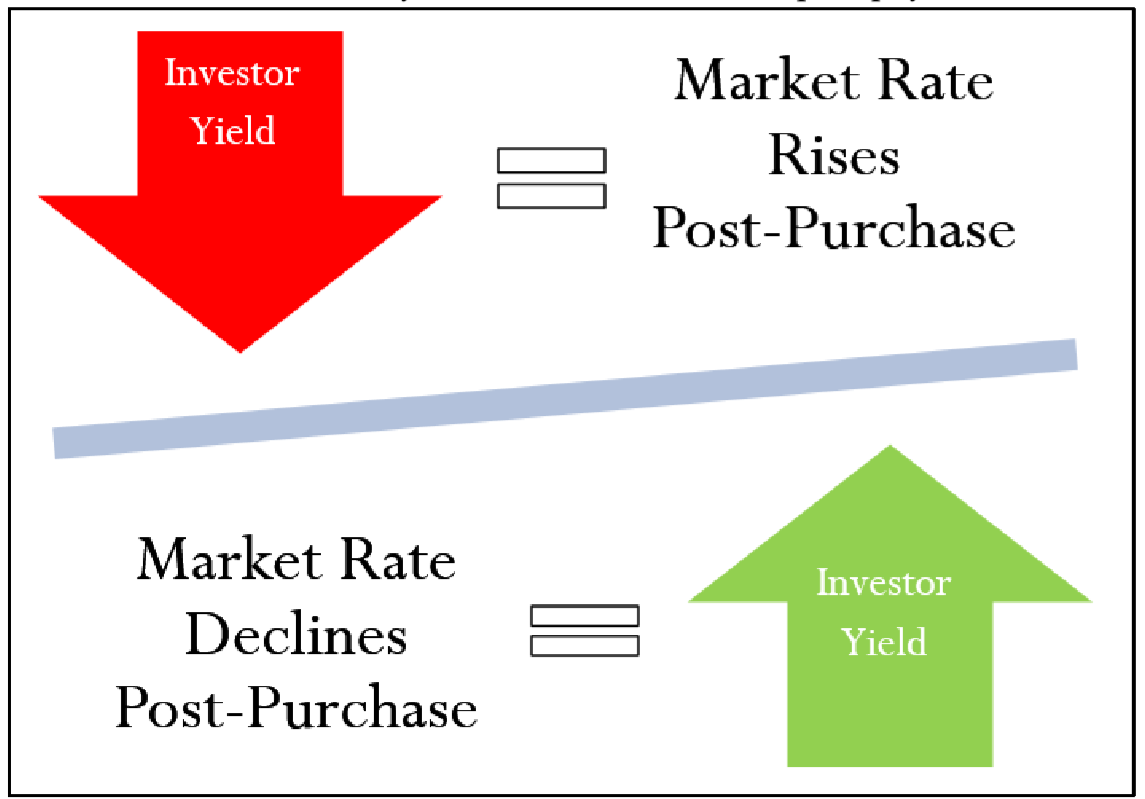
Figure \(\PageIndex{1}\): Investor's yield
The investor's yield consists of the coupon payments that have been received while the investor possesses the bond along with the difference achieved between the purchase price and the selling price. The above figure illustrates what happens to the investor’s yield by relating the post-purchase market rate and the investor's yield.
- When the market rate rises after the bond has been purchased, the investor experiences a lower yield than the original yield to maturity since the future bond selling price is reduced. Suppose that investors purchase the bond at a 5% market rate:
- If they hold it until maturity, they achieve a 5% yield to maturity.
- If they instead sell the bond before maturity when the market rate is 6%, the investor’s yield is less than 5%.
- When the market rate declines after the bond has been purchased, the investor experiences a higher yield than the original yield to maturity, since the future bond selling price is increased. Suppose again that investors purchase the bond at a 5% market rate:
- If they hold it until maturity, they of course achieve a 5% yield to maturity.
- If they sell the bond when the market rate is 4%, the investor’s yield is more than 5%.
The Formula
The existing bond formulas are sufficient for calculating the investor’s yield. You need Formula 14.2 to determine the bond coupon payment amount. You use Formula 14.3 to calculate both the purchase price and the selling price. You then use it a third time to solve for the periodic interest rate. When you solve for \(i\), the future value of the bond that you substitute into the formula must be the selling price of the bond at the future date, not the redemption price.
How It Works
Follow these steps to calculate the investor’s yield:

Step 1: Draw a timeline like the one depicted here, extending from the purchase date to the maturity date. Clearly indicate the selling date. Identify all known variables.
Step 2: Using Formula 14.2, calculate the amount of the bond interest payment.
Step 3: If needed, calculate the purchase price using Formula 14.3. As in previous procedures, use Formula 11.1 to calculate the semi-annually based \(N\) representing both the total number of compounds and the total number of payments. Use the market rate at the time of purchase.
Step 4: If needed, calculate the selling price using Formula 14.3 in the same manner. Use the market rate at the time of sale.
Step 5: Solve for the nominal rate of interest (\(IY\)) between the purchase date and the selling date. The purchase price is the date price, and the selling price is the future value (\(FV\)).
- If using a manual method, substitute all known numbers into Formula 14.3 and solve for the periodic interest rate (\(i\)). Convert it into a nominal interest rate using Formula 9.1.
- Alternatively, if using technology such as a calculator, then input all known variables and solve directly for the nominal interest rate (IY).
Important Notes
The same two requirements that applied to calculating yield to maturity persist when you calculate investor’s yield:
- Trading takes place only on interest payment dates.
- The bondholder reinvests all coupon payments at the same rate of interest.
In each of the following, determine whether the investor’s yield increases, decreases, or remains the same.
- A bond is purchased when the market yield is 5% and then sold when the market rate is 5%.
- A bond is purchased when the market yield is 5% and then sold when the market rate is 6%.
- Answer
-
- Increases; a lower market rate causes the selling price to rise.
- Same; no change in the market rate results in no change to the yield.
- Decreases; a higher market rate causes the selling price to decline
A $1,000 face value bond with a 7% coupon and 12 years to maturity was purchased for $1,084.68 when market rates were 6%. It sold seven years later for $920.87, when market rates were 9%. What yield did the bondholder realize?
Solution
The investor’s yield represents the nominal rate of interest on the bond during the time the investor owned the bond, or \(IY\).
What You Already Know
Step 1:
The timeline for the purchase and sale of the bond appears below.
Coupon Interest Payment: \(CPN\) = 7%, \(CY\) = 2, Face Value = $1,000 Purchase/Sale of
Bond: \(PV\) = $1,084.68, \(FV\) = $920.87, \(CY\) = 2, \(PMT_{BOND}\) = Formula 14.2, \(PY\) = 2, Years Held = 7
How You Will Get There
Step 2:
Apply Formula 14.2 to determine the periodic bond interest payment.
Step 3:
Determine the bond purchase price. It is known at $1,084.68 and does not need to be calculated. This is the date price for step 5.
Step 4:
Determine the bond selling price. It is known at $920.87 and does not need to be calculated. This is the future value (\(FV\)) for step 5.
Step 5:
Apply Formulas 11.1, 14.3, and 9.1 to determine the investor’s yield (\(IY\)). Solve Formulas 14.3 and 9.1 using your calculator.

Perform
Step 2:
\[PMT_{BOND}=\$ 1,000 \times \dfrac{0.07}{2}=\$ 35 \nonumber \]
Step 5:
\(N=2 \times 7=14\) (compounds and payments)
\[\$ 1,084.68=\dfrac{\$ 920.87}{(1+i)^{14}}+\$ 35\left[\dfrac{1-\left[\dfrac{1}{1+i}\right]^{14}}{i}\right] \quad i=\dfrac{I Y}{2} \nonumber \]
Calculator output \(= IY=4.6003 \%\)
Calculator Instructions
| Mode | N | I/Y | PV |
|---|---|---|---|
| END | 14 | Answer: 4.600320 | -1084.68 |
| PMT | FV | P/Y | C/Y |
|---|---|---|---|
| 35 | 920.87 | 2 | 2 |
The bond market price dropped significantly because of the 3% rise in the market rate over the seven-year time period. Thus, the investor does not realize the original yield to maturity of 6% (the market rate), and in fact the investor’s yield has dropped to 4.6003% compounded semi-annually.
In the opening discussions to Sections 14.1 and 14.2, you had invested in 10 Government of Canada $5,000 face value bonds with a 5% coupon and 20 years remaining to maturity, paying $4,699.02 each when prevailing bond rates were 5.5%. You notice today, 10 years later, that prevailing bond rates have dropped to 3.35%. What investor’s yield would you realize if you sold your bonds today?
Solution
You need to calculate the yield for just one of the 10 bonds since, of course, the yield is the same across all bonds. The investor’s yield represents the nominal rate of interest on the bond during the time you own the bond, or \(IY\).
What You Already Know
Step 1:
The timeline for purchase and sale of the bond appears below.
Coupon Interest Payment: \(CPN\) = 5%, \(CY\) = 2, Face Value = $5,000
Purchase of Bond: \(PV\) = $4,699.02
Sale of Bond: \(FV\) = $5,000, \(IY\) = 3.35%, \(CY\) = 2, \(PMT_{BOND}\) = Formula 14.2, \(PY\) = 2, Years Remaining = 10
Purchase/Sale of Bond: \(PV\) = $4,699.02, \(FV\) = Sale Price, \(CY\) = 2, \(PMT_{BOND}\) = Formula 14.2, \(PY\) = 2, Years Held = 10
How You Will Get There
Step 2:
Apply Formula 14.2 to determine the periodic bond interest payment.
Step 3:
Determine the bond purchase price. It is known at $4,699.02 and does not need to be calculated. This is the date price for step 5.
Step 4:
Determine the bond selling price by applying Formulas 9.1, 11.1, and 14.3. This is the future value (\(FV\)) for step 5.
Step 5:
Apply Formulas 11.1, 14.3, and 9.1 to determine the investor’s yield (\(IY\)). Solve Formulas 14.3 and 9.1 using the calculator.

Perform
Step 2:
\[PMT_{BOND}=\$ 5,000 \times \dfrac{0.05}{2}=\$ 125 \nonumber \]
Step 4:
\(i=3.35 \% / 2=1.675 \% ; N=2 \times 10=20\) (compounds and payments)
\[\text { Date Price }=\dfrac{\$ 5,000}{(1+0.01675)^{20}}+\$ 125\left[\dfrac{1-\left[\dfrac{1}{1+0.01675}\right]^{20}}{0.01675}\right]=\$ 5,696.14 \nonumber \]
Step 5:
\(N=2 \times 10=20 \) (compounds and payments)
\[\$ 4,699.02=\dfrac{\$ 5,696.14}{(1+i)^{20}}+\$ 125\left[\dfrac{1-\left[\dfrac{1}{1+i}\right]^{20}}{i}\right] \quad i=\dfrac{IY}{2} \nonumber \]
Calculator output \(=IY=6.8338 \%\)
Calculator Instructions
| Step | Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| 4 | END | 20 | 3.35 | Answer: 5,696.138252 | 125 | 5000 | 2 | 2 |
| 5 | \(\surd\) | \(\surd\) | Answer: 6.833820 | -4,699.02 | \(\surd\) | 5696.14 | \(\surd\) | \(\surd\) |
The bond market price increased significantly over the 10-year time period because the market rate dropped from 5.5% to 3.35%. Thus, the investor realizes more than the original yield to maturity of 5.5% (the market rate), and in fact the investor’s yield has risen to 6.8338% compounded semi-annually.


