Skip to main content
Mathematics LibreTexts

4.8: Graphing Functions (without using Calculus)

  1. Last updated
  2. Save as PDF
  • Page ID
    45170

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    There are some basic functions, called toolkit functions, that students should recognize by their function definition and their graph. For each of these functions, \(x\) is the input variable, and \(f(x)\) is the output variable. The following graphics are from the OER textbook Business Calculus by Calaway, Hoffman and Lippman, 2013 and are used with permission (Creative Commons Attribution 3.0 United States License).

    clipboard_ede6064ea442fb834e0fa0c313c7609ed.png
    Figure 4.8.1
    clipboard_eea23b266c3a3212da287a7aaf8144a98.png
    Figure 4.8.2

    Unlike a traditional STEM Calculus I course, this Calculus for Business and Social Sciences course does not teach graphing functions by using function transformations.

    Students in this class are expected to make a table of solutions and graph the function. Students will also learn how to graph functions using Calculus!

    Example 4.8.1

    Graph the following functions:

    1. \(f(x) = \sqrt[3]{x}\)
    2. \(f(x) = \dfrac{1 }{x^2 − 3}\)
    Solution
    1. Make a table of solutions and define the domain of the function.
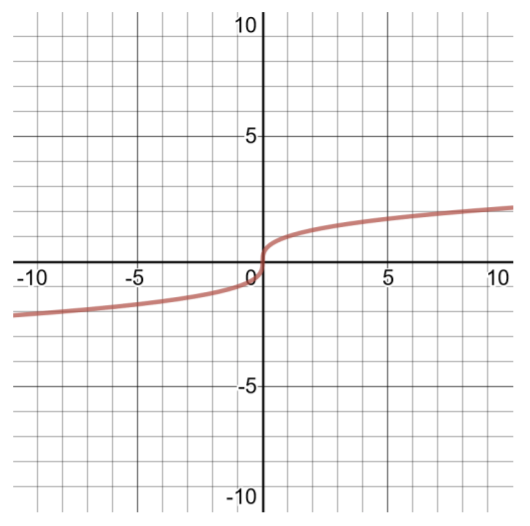
    clipboard_ed261280c100a11252bb366ad17622060.png
    Figure 4.8.3
    Table of Solutions for \(f(x) =\sqrt[3]{x}\) Domain \((−\infty , \infty )\)
    \(x\) \(f(x)\)
    -8 -2
    -1 -1
    0 0
    1 1
    8 2
    1. Make a table of solutions and define the domain of the function. To identify the domain of this rational function, pay attention to the denominator. The denominator cannot equal 0. Set the denominator = 0 to solve for x and find the values that will not be allowed for x.

    \(\begin{aligned} f(x) &= \dfrac{1 }{x^2 − 3}\\ 0 &= x^2 − 3 \\3 &= x^2 \\ \pm \sqrt{3} &=\sqrt{x^2} \\ \pm \sqrt{3}& = x \end{aligned}\)

    These numbers need to be excluded from the domain of this function \(−\sqrt{3}\) (about −1.732)) and \(\sqrt{3}\) (about 1.732)).

    To correctly graph this function, it’s important to examine the behavior around these numbers that are excluded from the domain. Thus, the reason for so many ordered pairs in the table of solutions. Think of it like this: start with a domain of \((−\infty , \infty )\), but must remove any numbers that will cause problems (like in this case, numbers that will cause the denominator of the function to be 0, because division by 0 is undefined). Graphing functions like this by hand is very tedious, but it’s an important skill for a student to have to succeed in Calculus for Business and Social Sciences.

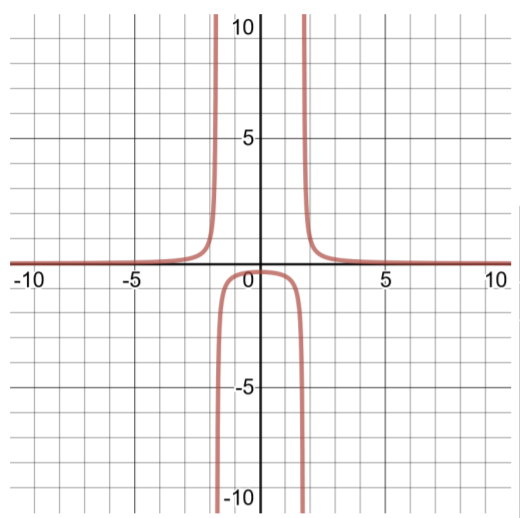
    clipboard_eb32340651fecc98bbbbf37f952e83529.png
    Figure 4.8.4
    Table of Solutions for \(f(x) = \sqrt[3]{ x}\) Domain \((−\infty , \infty )\)
    \(x\) \(f(x)\)
    -4 0.077
    -3 0.167
    -2 1
    -1.5 -1.333
    -1 -0.5
    -0.5 -0.364
    0 0
    0.5 -0.364
    1 -0.5
    1.5 -1.333
    2 1
    3 0.167
    4 0.077

    Practice Problems: Graph the following functions, paying attention to the domain of the function.

    1. \(f(x) = 2x^3\)
    2. \(f(x) = \dfrac{1 }{2x^2}\)
    3. \(f(x) = 4 \vert x − 2 \vert\)
    4. \(f(x) = \dfrac{1 }{3} x − 12 \)
    5. \(f(x) = \dfrac{1 }{x − 7}\)
    6. \(f(x) = 3\sqrt{2x^3 + 1}\)

    This page titled 4.8: Graphing Functions (without using Calculus) is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Victoria Dominguez, Cristian Martinez, & Sanaa Saykali (ASCCC Open Educational Resources Initiative) .