10.2: Solving and Graphing Inequalities, and Writing Answers in Interval Notation

Last updated
Save as PDF

Page ID: 45212

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

To solve and graph inequalities:

Solve the inequality using the Properties of Inequalities from the previous section.
Graph the solution set on a number line.
Write the solution set in interval notation.

Example 10.2.1

Solve the inequality, graph the solution set on a number line and show the solution set in interval notation:

$−1 ≤ 2x − 5 < 7$
$x^2 + 7x + 10 < 0$
$−6 < x − 2 < 4$

Solution

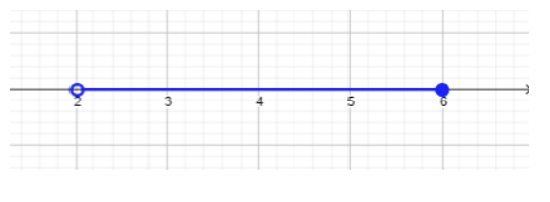
$\begin{array} &&−1 ≤ 2x − 5 < 7 &\text{Example problem} \\ &−1 + 5 ≤ 2x − 5 + 5 < 7 + 5 &\text{The goal is to isolate the variable \(x$, so start by adding $5$ to all three regions in the inequality.} \\ &4 ≤ 2x < 12 &\text{Simplify.} \\ &\dfrac{4}{2} ≤ 2x^2 < \dfrac{4}{2} &\text{Divide all by $2$ to isolate the variable $x$.} \\ &2 ≤ x < 6 &\text{Final answer written in inequality/solution set form.} \\ &[2, 6) &\text{Final answer written in interval notation (see section on Interval Notation for more details)} \end{array} \)

$clipboard_efc0262004238b3445893f014c353f830.png$

$\begin{array} &&x^2 + 7x + 10 < 0 &\text{Example problem} \\ &(x + 5)(x + 2) < 0 &\text{Factor the polynomial.} \\ &(x + 5)(x + 2) < 0 &\text{The product must be less than \(0$, which means that if $(x + 5) > 0$, then $(x + 2) < 0$. Similarly, if $(x + 5) < 0$, then $(x + 2) > 0$.} \\ &(x + 5) > 0 ∪ (x + 2) < 0 &\text{Find the intersection of each of these inequalities.} \\ &x > −5 ∪ x < −2 &\text{Find the intersection of each of these inequalities.} \end{array}\)

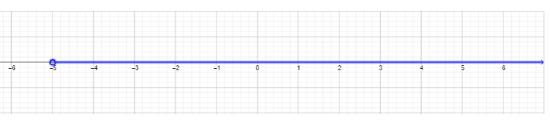
$\begin{array} &&\;\;\;−5 < x < −2 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\text{Final answer written in inequality/solution set form.} \\ &\;\;\;(−5, −2) \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\text{Final answer written in interval notation (see section on Interval Notation for more details).} \end{array}$

$\begin{array}&&−6 < x − 2 ≤ 4 &\text{Example problem} \\ &−6 + 2 < x − 2 + 2 ≤ 4 + 2 &\text{The goal is to isolate the variable \(x$, so start by adding $2$ to all three regions in the inequality.} \\ &−4 < x ≤ 6 &\text{Final answer written in inequality/solution set form.} \\ &(−4, 6] &\text{Final answer written in interval notation (see section on Interval Notation for more details).} \end{array}\)

$clipboard_e61db0750eee74347f74804dbd4b7221a.png$

Exercise 10.2.1

Solve the inequalities, graph the solution sets on a number line and show the solution sets in interval notation:

$0 ≤ x + 1 ≤ 4$
$0 < 2(x − 1) ≤ 4$
$6 < 2(x − 1) < 12$
$x^2 − 6x − 16 < 0$
$2x^2 − x − 15 > 0$