1.3: Understanding Venn Diagrams

Last updated
Save as PDF

Page ID: 129497

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In a residence, a cat is looking at tools, an instruction booklet for assembly, and pieces of furniture laid out on the floor. — Figure 1.6: When assembling furniture, instructions with images are easier to follow, just like how set relationships are easier to understand when depicted graphically. (credit: "Time to assemble more Ikea furniture!" by Rod Herrea/Flickr, CC BY 2.0)

Learning Objectives

After completing this section, you should be able to:

Utilize a universal set with two sets to interpret a Venn diagram.
Utilize a universal set with two sets to create a Venn diagram.
Determine the complement of a set.

Have you ever ordered a new dresser or bookcase that required assembly? When your package arrives you excitedly open it and spread out the pieces. Then you check the assembly guide and verify that you have all the parts required to assemble your new dresser. Now, the work begins. Luckily for you, the assembly guide includes step-by-step instructions with images that show you how to put together your product. If you are really lucky, the manufacturer may even provide a URL or QR code connecting you to an online video that demonstrates the complete assembly process. We can likely all agree that assembly instructions are much easier to follow when they include images or videos, rather than just written directions. The same goes for the relationships between sets.

Interpreting Venn Diagrams

Venn diagrams are the graphical tools or pictures that we use to visualize and understand relationships between sets. Venn diagrams are named after the mathematician John Venn, who first popularized their use in the 1880s. When we use a Venn diagram to visualize the relationships between sets, the entire set of data under consideration is drawn as a rectangle, and subsets of this set are drawn as circles completely contained within the rectangle. The entire set of data under consideration is known as the universal set.

Consider the statement: All trees are plants. This statement expresses the relationship between the set of all plants and the set of all trees. Because every tree is a plant, the set of trees is a subset of the set of plants. To represent this relationship using a Venn diagram, the set of plants will be our universal set and the set of trees will be the subset. Recall that this relationship is expressed symbolically as: $Trees \subset Plants .$ To create a Venn diagram, first we draw a rectangle and label the universal set “ $U = Plants .$ ” Then we draw a circle within the universal set and label it with the word “Trees.”

A single-set Venn diagram is shaded. Outside the set, it is labeled as 'Trees.' Outside the Venn diagram, 'U equals Plants' is labeled. — Figure 1.7:

This section will introduce how to interpret and construct Venn diagrams. In future sections, as we expand our knowledge of relationships between sets, we will also develop our knowledge and use of Venn diagrams to explore how multiple sets can be combined to form new sets.

Example 1.18: Interpreting the Relationship between Sets in a Venn Diagram

Write the relationship between the sets in the following Venn diagram, in words and symbolically.

A single-set Venn diagram is shaded. Outside the set, it is labeled as 'T equals Terriers.' Outside the Venn diagram, 'Parallelograms' is labeled. — Figure 1.8:

Answer: The set of terriers is a subset of the universal set of dogs. In other words, the Venn diagram depicts the relationship that all terriers are dogs. This is expressed symbolically as $T \subset U .$

Your Turn 1.18

Write the relationship between the sets in the following Venn diagram, in words and symbolically.

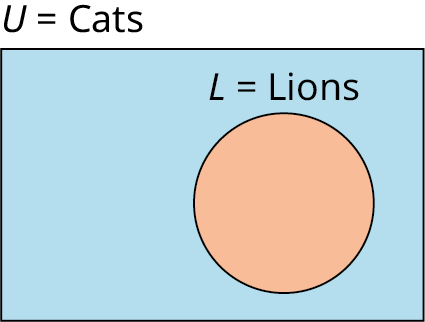
A single-set Venn diagram is shaded. Outside the set, it is labeled as 'L equals Lions.' Outside the Venn diagram, 'Parallelograms' is labeled. — Figure 1.9

So far, the only relationship we have been considering between two sets is the subset relationship, but sets can be related in other ways. Lions and tigers are both different types of cats, but no lions are tigers, and no tigers are lions. Because the set of all lions and the set of all tigers do not have any members in common, we call these two sets disjoint sets, or non-overlapping sets.

Two sets $A$ and $B$ are disjoint sets if they do not share any elements in common. That is, if $a$ is a member of set $A$ , then $a$ is not a member of set $B$ . If $b$ is a member of set $B$ , then $b$ is not a member of set $A$ . To represent the relationship between the set of all cats and the sets of lions and tigers using a Venn diagram, we draw the universal set of cats as a rectangle and then draw a circle for the set of lions and a separate circle for the set of tigers within the rectangle, ensuring that the two circles representing the set of lions and the set of tigers do not touch or overlap in any way.

A two-set Venn diagram not intersecting one another is given. Outside the Venn diagram, 'U equals Cats' is labeled. The first set is labeled T equals tigers while the second set is labeled L equals lions. — Figure 1.10:

Example 1.19: Describing the Relationship between Sets

Describe the relationship between the sets in the following Venn diagram.

A two-set Venn diagram not intersecting one another is given. Outside the Venn diagram, 'U equals 2D Figures' is labeled. The first set is labeled T equals Triangles while the second set is labeled S equals Squares. — Figure 1.11:

Answer: The set of triangles and the set of squares are two disjoint subsets of the universal set of two-dimensional figures. The set of triangles does not share any elements in common with the set of squares. No triangles are squares and no squares are triangles, but both squares and triangles are 2D figures.

Your Turn 1.19

Describe the relationship between the sets in the following Venn diagram.

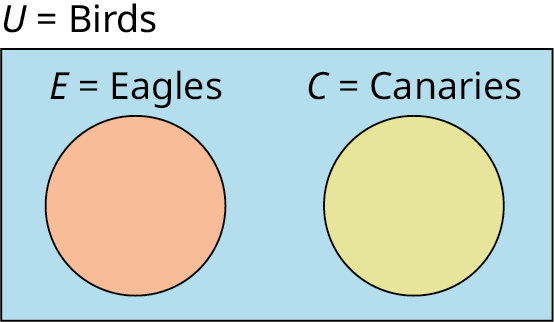
A two-set Venn diagram not intersecting one another is given. Outside the Venn diagram, 'U equals Birds' is labeled. The first set is labeled E equals Eagles while the second set is labeled C equals the Canaries. — Figure 1.12

Creating Venn Diagrams

The main purpose of a Venn diagram is to help you visualize the relationship between sets. As such, it is necessary to be able to draw Venn diagrams from a written or symbolic description of the relationship between sets.

Procedure

To create a Venn diagram:

Draw a rectangle to represent the universal set, and label it $U = set$ nameU=set name.
Draw a circle within the rectangle to represent a subset of the universal set and label it with the set name.

Checkpoint

If there are multiple disjoint subsets of the universal set, their separate circles should not touch or overlap.

Example 1.20: Drawing a Venn Diagram to Represent the Relationship Between Two Sets

Draw a Venn diagram to represent the relationship between each of the sets.

All rectangles are parallelograms.
All women are people.

Answer

The set of rectangles is a subset of the set of parallelograms.
First, draw a rectangle to represent the universal set and label it with $U =$ ParallelogramsU=Parallelograms, then draw a circle completely within the rectangle, and label it with the name of the set it represents, $R =$ RectanglesR=Rectangles.

A single-set Venn diagram is shaded. Outside the set, it is labeled 'R equals Rectangles.' Outside the Venn diagram shows, 'U equals Parallelograms.' — Figure 1.13:

In this example, both letters and names are used to represent the sets involved, but this is not necessary. You may use either letters or names alone, as long as the relationship is clearly depicted in the diagram, as shown below.

A single-set Venn diagram is shaded. Outside the set, it is labeled as 'Rectangles.' Outside the Venn diagram, 'Parallelograms' is labeled. — Figure 1.14:

A single-set Venn diagram is shaded. Outside the set, it is labeled as 'R.' Outside the Venn diagram, 'U' is labeled. — Figure 1.15:

The universal set is the set of people, and the set of all women is a subset of the set of people.

A single-set Venn diagram is shaded. Outside the set, it is labeled as 'Women.' Outside the Venn diagram, 'People' is labeled. — Figure 1.16:

Your Turn 1.20

Draw a Venn diagram to represent the relationship between each of the sets. All natural numbers are integers.

$A \subset U$. Draw a Venn diagram to represent this relationship.

Example 1.21: Drawing a Venn Diagram to Represent the Relationship Between Three Sets

All bicycles and all cars have wheels, but no bicycle is a car. Draw a Venn diagram to represent this relationship.

Answer

Step 1: The set of bicycles and the set of cars are both subsets of the set of things with wheels. The universal set is the set of things with wheels, so we first draw a rectangle and label it with $U = Things with$ WheelsU=Things with Wheels.

Step 2: Because the set of bicycles and the set of cars do not share any elements in common, these two sets are disjoint and must be drawn as two circles that do not touch or overlap with the universal set.

A two-set Venn diagram not intersecting one another is given. Outside the Venn diagram, 'U equals Things with Wheels' is labeled. The first set is labeled Bicycles while the second set is labeled Cars. — Figure 1.17:

Your Turn 1.21

Airplanes and birds can fly, but no birds are airplanes. Draw a Venn diagram to represent this relationship.

The Complement of a Set

Recall that if set $A$ is a proper subset of set $U$ , the universal set (written symbolically as $A \subset U$ ), then there is at least one element in set $U$ that is not in set $A$ . The set of all the elements in the universal set $U$ that are not in the subset $A$ is called the complement of set $A$ , $A'$ . In set builder notation this is written symbolically as: $A' = {x \in U | x \notin A} .$ The symbol $\in$ is used to represent the phrase, “is a member of,” and the symbol $\notin$ is used to represent the phrase, “is not a member of.” In the Venn diagram below, the complement of set $A$ is the region that lies outside the circle and inside the rectangle. The universal set $U$ includes all of the elements in set $A$ and all of the elements in the complement of set $A$ , and nothing else.

A single-set Venn diagram is shaded. Outside the set, it is labeled as 'A.' Outside the Venn diagram, 'U' is labeled. — Figure 1.18:

Consider the set of digit numbers. Let this be our universal set, $U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} .$ Now, let set $A$ be the subset of $U$ consisting of all the prime numbers in set $U$ , $A = {2, 3, 5, 7} .$ The complement of set $A$ is $A' = {0, 1, 4, 6, 8, 9} .$ The following Venn diagram represents this relationship graphically.

A single-set Venn diagram is labeled 'A equals (2, 3, 5, 7).' — Figure 1.19:

Example 1.22: Finding the Complement of a Set

For both of the questions below, $A$ is a proper subset of $U$.

1. Given the universal set $U=\{$ Billie Eilish, Donald Glover, Bruno Mars, Adele, Ed Sheeran\} and set $A=\{$ Donald Glover, Bruno Mars, Ed Sheeran $\}$, find $A^{\prime}$.

2. Given the universal set $U=\{\mathrm{d} \mid \mathrm{d}$ is a $\operatorname{dog}\}$ and $B=\{\mathrm{b} \in \mathrm{U} \mid \mathrm{b}$ is a beagle $\}$, find $B^{\prime}$.

Answer

1. The complement of set $A$ is the set of all elements in the universal set $U$ that are not in set $A$. $A^{\prime}=\{$ Billie Eilish, Adele $\}$.

2. The complement of set $B$ is the set of all dogs that are not beagles. All members of set $B^{\prime}$ are in the universal set because they are dogs, but they are not in set $B$, because they are not beagles. This relationship can be expressed in set build notation as follows:
$B^{\prime}=\{$ All dogs that are not beagles. $\}, B^{\prime}=\{d \in U \mid d$ is not a beagle. $\}$, or $B^{\prime}=\{d \in U \mid d \notin B\}$.

Your Turn 1.22

For both of the questions below, $A$ is a proper subset of $U$. 1. Given the universal set $U=\{$ red, orange, yellow, green, blue, indigo, violet $\}$ and set $A=\{$ yellow, red, blue $\}$, find $A^{\prime}$. 2. Given the universal set $U=\{c \mid c$ is a cat $\}$ and set $A=\{c \in U \mid c$ is not a lion $\}$, find $A^{\prime}$.

Check Your Understanding

A Venn diagram is a graphical representation of the _________ between sets.

In a Venn diagram, the set of all data under consideration, the _________ set, is drawn as a rectangle.

Two sets that do not share any elements in common are _________ sets.

The _________ of a subset $A$ or the universal set, $U$, is the set of all members of $U$ that are not in $A$.

The sets $A$ and $A^{\prime}$ are \_________ subsets of the universal set.

Section 1.3 Exercises

For the following exercises, interpret each Venn diagram and describe the relationship between the sets, symbolically and in words.

$A single-set Venn diagram is shaded. Outside the set, it is labeled as 'T equals Team sports.' Outside the Venn diagram, 'U equals Sports' is labeled.$

$A single-set Venn diagram is shaded. Outside the set, it is labeled as 'A equals Apples.' Outside the Venn diagram, 'U equals Fruit' is labeled.$

$A single-set Venn diagram is shaded. Outside the set is labeled 'P equals Pencils.' Outside the Venn diagram, 'U equals Writing Utensils' is labeled.$

$A single-set Venn diagram is labeled 'B equals Board Games'. Outside the Venn diagram, it is labeled as 'U equals Games.'$

$A two-set Venn diagram not intersecting one another is given. Outside the Venn diagram, 'U equals Writing Utensils' is labeled.$

$A two-set Venn diagram not intersecting one another is given. Outside the Venn diagram, 'U equals Fruit' is labeled.$

$A two-set Venn diagram not intersecting one another is given. Outside the Venn diagram, it is labeled as 'U equals Writing Games.' The first set is labeled A equals Card games while the second set is labeled B equals Video Games.$

$A two-set Venn diagram not intersecting one another is given. Outside the Venn diagram, it is labeled as 'U equals Investments.' The first set is labeled A equals Stocks while the second set is labeled B equals Bonds.$

For the following exercises, create a Venn diagram to represent the relationships between the sets.

9. All birds have wings.

10. All cats are animals.

11. All almonds are nuts, and all pecans are nuts, but no almonds are pecans.

12. All rectangles are quadrilaterals, and all trapezoids are quadrilaterals, but no rectangles are trapezoids.

13. Lizards $\subset$ Reptiles.

14. Ladybugs $\subset$ Insects.

15. Ladybugs $\subset$ Insects and Ants $\subset$ Insects, but no Ants are Ladybugs.

16. Lizards $\subset$ Reptiles and Snakes $\subset$ Reptiles, but no Lizards are Snakes.

17. $A$ and $B$ are disjoint subsets of $U$.

18. $C$ and $D$ are disjoint subsets of $U$.

19. $T$ is a subset of $U$.

20. $S$ is a subset of $U$.

21. $J=$ Jazz, $M=$ Music, and $J \subset M$.

22. $R=$ Reggae, $M=$ Music, and $R \subset M$.

23. $J=$ Jazz, $R=$ Reggae, and $M=$ Music are sets with the following relationships: $J \subset M, R \subset M$, and $R$ is disjoint from $J$.

24. $J=$ Jazz, $B=$ Bebop, and $M=$ Music are sets with the following relationships: $J \subset M$ and $B \subset J$.

For the following exercises, the universal set is the set of single digit numbers, $U=\{0,1,2,3,4,5,6,7,8,9\}$. Find the complement of each subset of $U$.
25. $A=\{6,7,8\}$

26. $A=\{0,2,4,6,8\}$

27. $A=\{ \}$

28. $A=\{0,1,4,6,8,9\}$

29. $A=\{0,1,2,3,4,5,6,7,8,9\}$

30. $A=\{0,1,3,4,5,6,7,9\}$

31. $A=\{1,2,3,4,5,6,7,8,9\}$

32. $A=\{0,3,6,9\}$

For the following exercises, the universal set is $U=$ \{Bashful, Doc, Dopey, Grumpy, Happy, Sleepy, Sneezy\}. Find the complement of each subset of $U$.

33. $A=\{$ Happy, Bashful, Grumpy\}

34. $A=\{$ Sleepy, Sneezy $\}$

35. $A=\{\mathrm{Doc}\}$

36. $A=\{$ Doc, Dopey $\}$

37. $A=\emptyset$

38. $A=\{$ Doc, Grumpy, Happy, Sleepy, Bashful, Sneezy, Dopey\}

For the following exercises, the universal set is $U=\mathbb{N}=\{1,2,3, \ldots\}$. Find the complement of each subset of $U$.

39. $A=\{1,2,3,4,5\}$

40. $A=\{1,3,5, \ldots\}$

41. $A=\{1\}$

42. $A=\{4,5,6, \ldots\}$

For the following exercises, use the Venn diagram to determine the members of the complement of set $A, A^{\prime}$.

$A single-set Venn diagram is labeled 'A equals (2, 3, 4, 9).' Outside the Venn diagram, the union of the Venn diagram is marked 'U equals (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).'$

44.

$A single-set Venn diagram is labeled 'A equals (2, 3, 4, 9).' Outside the Venn diagram, the union of the Venn diagram is marked 'U equals (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).'$

45.

$A single-set Venn diagram is labeled A equals (n, e, t). Outside the Venn diagram, the union of the Venn diagram is marked 'U equals (l, i, s, t, e, n).'$

46.

$A single-set Venn diagram is labeled 'A equals (l, i, n, e, s).' Outside the Venn diagram, the union of the Venn diagram is marked 'U equals (l, i, s, t, e, n).'$

Search

Text Color

Text Size

Margin Size

Font Type

Example 1.18: Interpreting the Relationship between Sets in a Venn Diagram

Your Turn 1.18

Example 1.19: Describing the Relationship between Sets

Your Turn 1.19

Checkpoint

Example 1.20: Drawing a Venn Diagram to Represent the Relationship Between Two Sets

Your Turn 1.20

Example 1.21: Drawing a Venn Diagram to Represent the Relationship Between Three Sets

Your Turn 1.21

Example 1.22: Finding the Complement of a Set

Your Turn 1.22