10.8: Right Triangle Trigonometry

Figure $\PageIndex{1}$: In the lower left corner of the fresco The School of Athens by Raphael, the figure in white writing in the book represents Pythagoras. Alongside him, to the right, the figure with the long, light-brown hair is said to depict Archimedes. (credit: modification of work “School of Athens” by Raphael (1483–1520), Vatican Museums/Wikimedia, Public Domain)

Learning Objectives

1. Apply the Pythagorean Theorem to find the missing sides of a right triangle.
2. 2. Apply the $30^{\circ}-60^{\circ}-90^{\circ}$ and $45^{\circ}-45^{\circ}-90^{\circ}$ right triangle relationships to find the missing sides of a triangle.
3. Apply trigonometric ratios to find missing parts of a right triangle.
4. Solve application problems involving trigonometric ratios.

This is another excerpt from Raphael’s The School of Athens. The man writing in the book represents Pythagoras, the namesake of one of the most widely used formulas in geometry, engineering, architecture, and many other fields, the Pythagorean Theorem. However, there is evidence that the theorem was known as early as 1900–1100 BC by the Babylonians. The Pythagorean Theorem is a formula used for finding the lengths of the sides of right triangles.

Born in Greece, Pythagoras lived from 569–500 BC. He initiated a cult-like group called the Pythagoreans, which was a secret society composed of mathematicians, philosophers, and musicians. Pythagoras believed that everything in the world could be explained through numbers. Besides the Pythagorean Theorem, Pythagoras and his followers are credited with the discovery of irrational numbers, the musical scale, the relationship between music and mathematics, and many other concepts that left an immeasurable influence on future mathematicians and scientists.

The focus of this section is on right triangles. We will look at how the Pythagorean Theorem is used to find the unknown sides of a right triangle, and we will also study the special triangles, those with set ratios between the lengths of sides. By ratios we mean the relationship of one side to another side. When you think about ratios, you should think about fractions. A fraction is a ratio, the ratio of the numerator to the denominator. Finally, we will preview trigonometry. We will learn about the basic trigonometric functions, sine, cosine and tangent, and how they are used to find not only unknown sides but unknown angles, as well, with little information.

Pythagorean Theorem

The Pythagorean Theorem is used to find unknown sides of right triangles. The theorem states that the sum of the squares of the two legs of a right triangle equals the square of the hypotenuse (the longest side of the right triangle).

FORMULA

The Pythagorean Theorem states

$$a^2+b^2=c^2 \nonumber$$

where $a$ and $b$ are two sides (legs) of a right triangle and $c$ is the hypotenuse, as shown in Figure $\PageIndex{2}$

Figure $\PageIndex{2}$: Pythagorean Right Triangle

For example, given that side $a=6,$ and side $b=8,$ we can find the measure of side $c$ using the Pythagorean Theorem. Thus,

$$\begin{aligned} a^2+b^2 & =c^2 \\ (6)^2+(8)^2 & =c^2 \\ 36+64 & =c^2 \\ 100 & =c^2 \\ \sqrt{100} & =\sqrt{c^2} \\ 10 & =c \end{aligned} \nonumber$$

Example $\PageIndex{1}$: Using the Pythagorean Theorem

Find the length of the missing side of the triangle (Figure $\PageIndex{3}$ ).

Figure $\PageIndex{3}$

Answer

Using the Pythagorean Theorem, we have

\[\begin{aligned}
(6)^2+b^2 & =(14)^2 \
36+b^2 & =196 \
b^2 & =196-36 \
b^2 & =160 \
b & = \pm \sqrt{160} \
& =4 \sqrt{10}=12.65
\end{aligned \nonumber \]

When we take the square root of a number, the answer is usually both the positive and negative root. However, lengths cannot be negative, which is why we only consider the positive root.
$$\begin{array}{c}\hfill \end{array}$$

Your Turn $\PageIndex{1}$

Use the Pythagorean Theorem to find the missing side of the right triangle shown.

Figure $\PageIndex{4}$

Distance

The applications of the Pythagorean Theorem are countless, but one especially useful application is that of distance. In fact, the distance formula stems directly from the theorem. It works like this:

In Figure

$$\begin{aligned} d & =\sqrt{(3-(-3))^2+(2-(-1))^2} \\ & =\sqrt{(6)^2+(3)^2}=\sqrt{36+9} \\ & =\sqrt{45}=3 \sqrt{5}=6.7 \end{aligned} \nonumber$$

Thus, $d=c$, the hypotenuse, in the Pythagorean Theorem.

Figure $\PageIndex{5}$ : Distance

Example $\PageIndex{2}$: Calculating Distance Using the Distance Formula

You live on the corner of First Street and Maple Avenue, and work at Star Enterprises on Tenth Street and Elm Drive (Figure $\PageIndex{6}$ ). You want to calculate how far you walk to work every day and how it compares to the actual distance (as the crow flies). Each block measures 200 ft by 200 ft.

Figure $\PageIndex{6}$

Answer

You travel 7 blocks south and 9 blocks west. If each block measures 200 ft by 200 ft , then $9(200)+7(200)=1,800 \mathrm{ft}+1,400 \mathrm{ft}=3,200 \mathrm{ft}$.

As the crow flies, use the distance formula. We have

$$\begin{aligned} d & =\sqrt{(1,800-0)^2+(1,400-0)^2} \\ & =\sqrt{3,240,000+1,960,000} \\ & =\sqrt{5,200,000} \\ & =2280.4 \mathrm{ft} \end{aligned} \nonumber$$
$$\begin{array}{c}\hfill \end{array}$$

Your Turn $\PageIndex{2}$

How far is it to your workplace (as the crow flies) if the blocks in the previous example measure 100 ft by 100 ft?

Example $\PageIndex{3}$: Calculating Distance with the Pythagorean Theorem

The city has specific building codes for wheelchair ramps. Every vertical rise of 1 in requires that the horizontal length be 12 inches. You are constructing a ramp at your business. The plan is to make the ramp 130 inches in horizontal length and the slanted distance will measure approximately 132.4 inches (Figure $\PageIndex{7}$). What should the vertical height be?

Figure $\PageIndex{7}$

Answer

The Pythagorean Theorem states that the horizontal length of the base of the ramp, side a, is 130 in. The length of c, or the length of the hypotenuse, is

The Pythagorean Theorem states that the horizontal length of the base of the ramp, side $a$, is 130 in . The length of $c$, or the length of the hypotenuse, is 132.4 in . The length of the height of the triangle is side $b$.

Then, by the Pythagorean Theorem, we have:

$$\begin{aligned} a^2+b^2 & =c^2 \\ (130)^2+b^2 & =(132.4)^2 \\ 16,900+b^2 & =17,529.76 \\ b^2 & =17,529.76-16,900 \\ b^2 & =629.8 \\ b & =\sqrt{629.8}=25 \end{aligned} \nonumber$$

If you construct the ramp with a 25 in vertical rise, will it fulfill the building code? If not, what will have to change?

The building code states 12 in of horizontal length for each 1 in of vertical rise. The vertical rise is 25 in, which means that the horizontal length has to be $12(25)=300 \mathrm{in}$. So, no, this will not pass the code. If you must keep the vertical rise at 25 in , what will the other dimensions have to be? Since we need a minimum of 300 in for the horizontal length:

$$\begin{aligned} (300)^2+(25)^2 & =c^2 \\ 90,625 & =c^2 \\ \sqrt{90,625} & =c=301 \mathrm{in} \end{aligned} \nonumber$$
$$\begin{array}{c}\hfill \end{array}$$

The new ramp will look like Figure 10.185.

Figure $\PageIndex{8}$

Your Turn $\PageIndex{3}$

If 10 in is the maximum possible vertical rise as shown in the figure, how long would the ramp have to be to pass the building code rule of 12 horizontal inches to 1 vertical inch?

Figure $\PageIndex{9}$

${30}^{\circ }\text{-}{60}^{\circ }\text{-}{90}^{\circ }$ Triangles

In geometry, as in all fields of mathematics, there are always special rules for special circumstances. An example is the perfect square rule in algebra. When expanding an expression like $(2 x+5 y)^2$, we do not have to expand it the long way:

$$\begin{aligned} (2 x+5 y)^2 & =(2 x+5 y)(2 x+5 y) \\ & =(2 x)^2+10 x y+10 x y+(5 y)^2 \\ & =4 x^2+20 x y+25 y^2 \end{aligned} \nonumber$$

If we know the perfect square formula, given as

$$(a+b)^2=a^2+2 a b+b^2 \nonumber$$

we can skip the middle step and just start writing down the answer. This may seem trivial with problems like $(a+b)^2$. However, what if you have a problem like $(2 \sqrt{3}+3 \sqrt[3]{31.8 c})^2$ ? That is a different story. Nevertheless, we use the same perfect square formula. The same idea applies in geometry. There are special formulas and procedures to apply in certain types of problems. What is needed is to remember the formula and remember the kind of problems that fit. Sometimes we believe that because a formula is labeled special, we will rarely have use for it. That assumption is incorrect. So, let us identify the $30^{\circ}-60^{\circ}-90^{\circ}$ triangle and find out why it is special. See Figure $\PageIndex{10}$.

Figure $\PageIndex{10}$: The $30^{\circ }\text{-}60^{\circ }\text{-}90^{\circ }$

We see that the shortest side is opposite the smallest angle, and the longest side, the hypotenuse, will always be opposite the right angle. There is a set ratio of one side to another side for the $30^{\circ}-60^{\circ}-90^{\circ}$ triangle given as $1: \sqrt{3}: 2$, or $x: x \sqrt{3}: 2 x$. Thus, you only need to know the length of one side to find the other two sides in a $30^{\circ}-60^{\circ}-90^{\circ}$ triangle.

Example $\PageIndex{4}$: Finding Missing Lengths in a $30^{\circ }\text{-}60^{\circ }\text{-}90^{\circ }$ Triangle

Find the measures of the missing lengths of the triangle (Figure $\PageIndex{11}$).

Figure $\PageIndex{11}$

Answer

We can see that this is a $30^{\circ}-60^{\circ}-90^{\circ}$ triangle because we have a right angle and a $30^{\circ}$ angle. The remaining angle, therefore, must equal $60^{\circ}$. Because this is a special triangle, we have the ratios of the sides to help us identify the missing lengths. Side $a$ is the shortest side, as it is opposite the smallest angle $30^{\circ}$, and we can substitute $a=x$. The ratios are $x: x \sqrt{3}: 2 x$. We have the hypotenuse equaling 10 , which corresponds to side $c$, and side $c$ is equal to $2 x$. Now, we must solve for $x$ :

$$\begin{aligned} 2 x & =10 \\ x & =5 \end{aligned} \nonumber$$

Side $b$ is equal to $x \sqrt{3}$ or $5 \sqrt{3}$. The lengths are $5,5 \sqrt{3}, 10$.$\mathrm{}$

Your Turn $\PageIndex{4}$

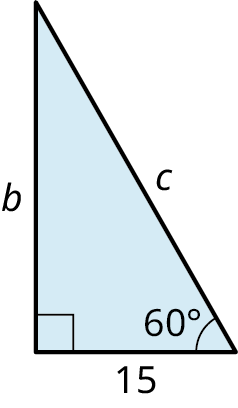
Find the lengths of the missing sides in the given figure.

Figure $\PageIndex{12}$

Example $\PageIndex{5}$: Applying $30^{\circ }\text{-}60^{\circ }\text{-}90^{\circ }$ Triangle to the Real World

A city worker leans a 40-foot ladder up against a building at a $30^{\circ}$ angle to the ground (Figure $\PageIndex{13}$). How far up the building does the ladder reach?

Figure $\PageIndex{13}$

Answer

We have a $30^{\circ}-60^{\circ}-90^{\circ}$ triangle, and the hypotenuse is 40 ft . This length is equal to $2 x$, where $x$ is the shortest side. If $2 x=40$, then $x=20$. The ladder is leaning on the wall 20 ft up from the ground.

Your Turn $\PageIndex{5}$

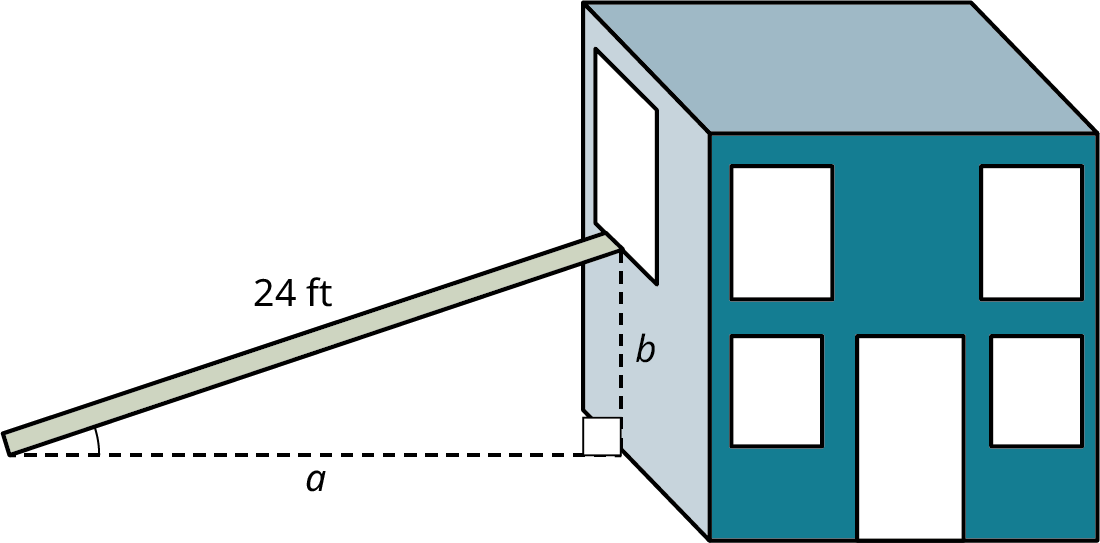
You want to repair a window on the second floor of your home. If you place the ladder at a ${30^ \circ }$ angle to the ground, the ladder just about reaches the window. How far from the wall should you place the ladder? How far up will the ladder reach? Make a sketch as an aid.

Figure $\PageIndex{14}$

$45^{\circ }\text{-}45^{\circ }\text{-}90^{\circ }$ Triangles

The $45^{\circ}-45^{\circ}-90^{\circ}$ triangle is another special triangle such that with the measure of one side we can find the measures of all the sides. The two angles adjacent to the $90^{\circ}$ angle are equal, and each measures $45^{\circ}$. If two angles are equal, so are their opposite sides. The ratio among sides is $1: 1: \sqrt{2}$, or $x: x: x \sqrt{2}$, as shown in Figure $\PageIndex{15}$.

Figure $\PageIndex{15}$: $45^{\circ }\text{-}45^{\circ }\text{-}90^{\circ }$ Triangles

Example $\PageIndex{6}$: Finding Missing Lengths of a $45^{\circ }\text{-}45^{\circ }\text{-}90^{\circ }$ Triangle

Find the measures of the unknown sides in the triangle (Figure 10.193).

Figure $\PageIndex{16}$

Answer

Because we have a $45^{\circ}-45^{\circ}-90^{\circ}$ triangle, we know that the two legs are equal in length and the hypotenuse is a product of one of the legs and $\sqrt{2}$. One leg measures 3 , so the other leg, $a$, measures 3 . Remember the ratio of $x: x: x \sqrt{2}$. Then, the hypotenuse, $c$, equals $3 \sqrt{2}$.$$

Your Turn $\PageIndex{6}$

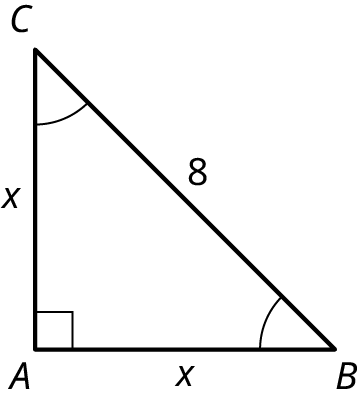
Find the measures of the unknown sides in the given figure.

Figure $\PageIndex{17}$

Trigonometry Functions

Trigonometry developed around 200 BC from a need to determine distances and to calculate the measures of angles in the fields of astronomy and surveying. Trigonometry is about the relationships (or ratios) of angle measurements to side lengths in primarily right triangles. However, trigonometry is useful in calculating missing side lengths and angles in other triangles and many applications.

Checkpoint

NOTE: You will need either a scientific calculator or a graphing calculator for this section. It must have the capability to calculate trigonometric functions and express angles in degrees.

Trigonometry is based on three functions. We title these functions using the following abbreviations:
- $\sin =\operatorname{sine}$
- $\cos =$ cosine
- $\tan =$ tangent

Letting $r=\sqrt{x^2+y^2}$, which is the hypotenuse of a right triangle, we have Table 10.1. The functions are given in terms of $x, y$, and $r$, and in terms of sides relative to the angle, like opposite, adjacent, and the hypotenuse.

Table $\PageIndex{1}$ Trigonometric Ratios

$$\begin{array}{l|l|l} \sin \theta=\frac{y}{r}=\frac{o p p}{h y p} & \cos \theta=\frac{x}{r}=\frac{a d j}{h y p} & \tan \theta=\frac{y}{x}=\frac{o p p}{a d j} \end{array} \nonumber$$

We will be applying the sine function, cosine function, and tangent function to find side lengths and angle measurements for triangles we cannot solve using any of the techniques we have studied to this point. In Figure $\PageIndex{18}$, we have an illustration mainly to identify $r$ and the sides labeled $x$ and $y$.

Figure $\PageIndex{18}$: Angle θθ

An angle $\theta$ sweeps out in a counterclockwise direction from the positive $x$-axis and stops when the angle reaches the desired measurement. That ray extending from the origin that marks $\theta^{\circ}$ is called the terminal side because that is where the angle terminates. Regardless of the information given in the triangle, we can find all missing sides and angles using the trigonometric functions. For example, in Figure $\PageIndex{19}$, we will solve for the missing sides.

Figure $\PageIndex{19}$: Solving for Missing Sides

Let’s use the trigonometric functions to find the sides $x$ and $y$. As long as your calculator mode is set to degrees, you do not have to enter the degree symbol. First, let’s solve for $y$.

We have $\sin \theta=\dfrac{y}{r}$, and $\theta=60^{\circ}$. Then,

$$\begin{aligned} \sin 60^{\circ} & =\dfrac{y}{2} \\ 2 \sin 60^{\circ} & =y \\ 1.732 & =y \\ \sqrt{3} & =y \end{aligned} \nonumber$$

Next, let's find $x$. This is the cosine function. We have $\cos \theta=\dfrac{x}{r}$. Then,

$$\begin{aligned} \cos 60^{\circ} & =\dfrac{x}{2} \\ 2 \cos 60^{\circ} & =x \\ & =1 \end{aligned} \nonumber$$

Now we have all sides, $1, \sqrt{3}, 2$. You can also check the sides using the $30^{\circ}-60^{\circ}-90^{\circ}$ ratio of $1: \sqrt{3}: 2$. Table 10.2 is a list of common angles, which you should find helpful. Table 10.2 is a list of common angles, which you should find helpful.

Table 10.2 Common Angles

$\sin 0^{\circ}=0$	$\cos 0^{\circ}=1$
$\sin 30^{\circ}=\dfrac{1}{2}$	$\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$
$\sin 45^{\circ}=\dfrac{\sqrt{2}}{2}$	$\cos 45^{\circ}=\dfrac{\sqrt{2}}{2}$
$\sin 60^{\circ}=\dfrac{\sqrt{3}}{2}$	$\cos 60^{\circ}=\dfrac{1}{2}$
$\sin 90^{\circ}=1$	$\cos 90^{\circ}=0$

Example $\PageIndex{7}$: Using Trigonometric Functions

Find the lengths of the missing sides for the triangle (Figure $\PageIndex{20}$).

Figure $\PageIndex{20}$

Answer

We have a $55^{\circ}$ angle, and the length of the triangle on the $x$-axis is 6 units.

Step 1: To find the length of $r$, we can use the cosine function, as $\cos \theta=\frac{x}{r}$. We manipulate this equation a bit to solve for $r$ :

$$\begin{aligned} \cos \left(55^{\circ}\right) & =\frac{6}{r} \\ r \cos \left(55^{\circ}\right) & =6 \\ r & =\frac{6}{\cos \left(55^{\circ}\right)} \\ r & =\frac{6}{0.5736}=10.46 \end{aligned} \nonumber$$

Step 2: We can use the Pythagorean Theorem to find the length of $y$. Prove that your answers are correct by using other trigonometric ratios:

$$\begin{aligned} 6^2+y^2 & =10.46^2 \\ y^2 & =109.4-36 \\ y & =8.57 \end{aligned} \nonumber$$

Step 3: Now that we have $y$, we can use the sine function to prove that $r$ is correct. We have $\sin \theta=\frac{y}{r}$.

$$\begin{aligned} \sin \left(55^{\circ}\right) & =\frac{8.57}{r} \\ r \sin \left(55^{\circ}\right) & =8.57 \\ r & =\frac{8.57}{\sin \left(55^{\circ}\right)} \\ & =\frac{8.57}{0.819}=10.46 \end{aligned} \nonumber$$
$$\begin{array}{c}\mathrm{}\hfill \end{array}$$

Your Turn $\PageIndex{7}$

Find the lengths of the missing sides in the given figure.

Figure $\PageIndex{21}$

To find angle measurements when we have two side measurements, we use the inverse trigonometric functions symbolized as $\sin ^{-1}, \cos ^{-1}$, or $\tan ^{-1}$. The -1 looks like an exponent, but it means inverse. For example, in the previous example, we had $x=6$ and $r=10.46$. To find what angle has these values, enter the values for the inverse cosine function $\cos ^{-1}\left(\frac{x}{r}\right)$ in your calculator:

$$\cos ^{-1}\left(\frac{6}{10.46}\right)=55^{\circ} \nonumber$$

You can also use the inverse sine function and enter the values of $\sin ^{-1}\left(\frac{y}{r}\right)$ in your calculator given $y=8.57$ and $r=10.46$. We have

$$\sin ^{-1}\left(\frac{8.57}{10.46}\right)=55^{\circ} \nonumber$$

Finally, we can also use the inverse tangent function. Recall $\tan \theta=\frac{y}{x}$. We have

$$\tan ^{-1}\left(\frac{8.57}{6}\right)=55^{\circ} \nonumber$$

$$$$

Example $\PageIndex{8}$: Solving for Lengths in a Right Triangle

Solve for the lengths of a right triangle in which $\theta=30^{\circ}$ and $r=6$ (Figure $\PageIndex{22}$).

Figure $\PageIndex{22}$

Answer

Step 1: To find side $a$, we use the sine function:

$$\begin{aligned} \sin 30^{\circ} & =\frac{a}{6} \\ 6 \sin 30^{\circ} & =a=3 \end{aligned} \nonumber$$

Step 2: To find $b$, we use the cosine function:

$$\begin{aligned} \cos 30^{\circ} & =\frac{b}{6} \\ 6 \cos 30^{\circ} & =b=5.196 \end{aligned} \nonumber$$

Step 3: Since this is a $30^{\circ}-60^{\circ}-90^{\circ}$ triangle and side $b$ should equal $x \sqrt{3}$, if we input 3 for $x$, we have $b=3 \sqrt{3}$. Put this in your calculator and you will get $3 \sqrt{3}=5.196$.

$\mathrm{}$

Your Turn $\PageIndex{8}$

Find the missing side and angles in the figure shown.

Figure $\PageIndex{23}$

Example $\PageIndex{9}$: Finding Altitude

A small plane takes off from an airport at an angle of $31.3^{\circ}$ to the ground. About two-thirds of a mile $(3,520 \mathrm{ft})$ from the airport is an 1,100-ft peak in the flight path of the plane (Figure \(\PageIndex{24}\)). If the plane continues that angle of ascent, find its altitude when it is above the peak, and how far it will be above the peak.

Figure $\PageIndex{24}$

Answer

To solve this problem, we use the tangent function:

$$\begin{aligned} \tan 31.3^{\circ} & =\frac{x}{3,520} \\ 3,520 \tan 31.3^{\circ} & =2,140 \end{aligned} \nonumber$$

The plane's altitude when passing over the peak is $2,140 \mathrm{ft}$, and it is $1,040 \mathrm{ft}$ above the peak.

Your Turn $\PageIndex{9}$

Suppose that the plane takes off at a ${23^ \circ }$ angle, and 1 mile from the airport is a 1,500-foot peak. At what altitude will the plane pass over the peak?

Example $\PageIndex{10}$: Finding Unknown Sides and Angles

Suppose you have two known sides, but do not know the measure of any angles except for the right angle (Figure $\PageIndex{25}$)). Find the measure of the unknown angles and the third side.

Figure $\PageIndex{25}$

Answer

Step 1: We can find the third side using the Pythagorean Theorem:

$$\begin{aligned} 6^2+4^2 & =c^2 \\ 52 & =c^2 \\ 2 \sqrt{13} & =c \end{aligned} \nonumber$$

Now, we have all three sides.

Step 2: To find $\theta$, we will first find $\sin \theta$.

$$\begin{aligned} \sin \theta & =\frac{o p p}{h y p} \\ & =\frac{4}{2 \sqrt{13}} \\ & =\frac{2}{\sqrt{13}} \end{aligned} \nonumber$$

The angle $\theta$ is the angle whose sine is $\frac{2}{\sqrt{13}}$.

Step 3: To find $\theta$, we use the inverse sine function:

$$\begin{aligned} \theta & =\sin ^{-1}\left(\frac{2}{\sqrt{13}}\right) \\ & =33.7^{\circ} \end{aligned} \nonumber$$

Step 4: To find the last angle, we just subtract: $180^{\circ}-90^{\circ}-33.7^{\circ}=56.3^{\circ}$.

Your Turn $\PageIndex{10}$

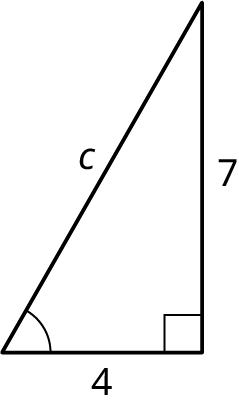
You know the lengths of two sides and the right angle as shown in the figure. Find the length of the third side and the other angles.

Figure $\PageIndex{26}$

Angle of Elevation and Angle of Depression

Other problems that involve trigonometric functions include calculating the angle of elevation and the angle of depression. These are very common applications in everyday life. The angle of elevation is the angle formed by a horizontal line and the line of sight from an observer to some object at a higher level. The angle of depression is the angle formed by a horizontal line and the line of sight from an observer to an object at a lower level.

Example $\PageIndex{11}$: Finding the Angle of Elevation

A guy wire of length 110 meters runs from the top of an antenna to the ground (Figure $\PageIndex{27}$). If the angle of elevation of an observer to the top of the antenna is ${43}^{\circ },$ how high is the antenna?

Figure \(\PageIndex{27}\)

Answer

We are looking for the height of the tower. This corresponds to the $y$-value, so we will use the sine function:

$$\begin{aligned} \sin 43^{\circ} & =\frac{y}{110} \\ 110 \sin 43^{\circ} & =y \\ 75 & =y \end{aligned} \nonumber$$
$$\begin{array}{c}\hfill \end{array}$$

The tower is 75 m high.

Your Turn $\PageIndex{11}$

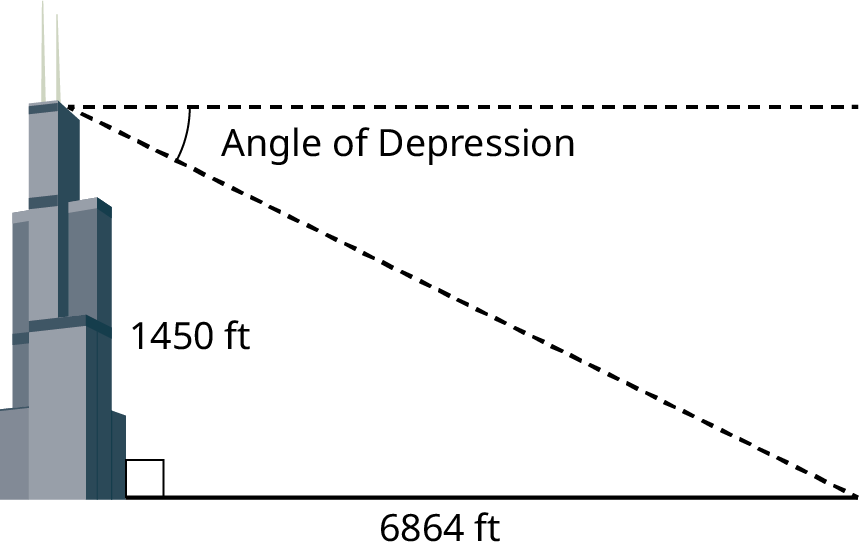
You travel to Chicago and visit the observation deck at Willis Tower, 1,450 ft above ground. You can see the Magnificent Mile to the northeast 6,864 ft away. What is the angle of depression from the observation deck to the Magnificent Mile?

Figure \(\PageIndex{28}\)

Example $\PageIndex{12}$: Finding Angle of Elevation

You are sitting on the grass flying a kite on a 50-foot string (Figure \(\PageIndex{29}\)). The angle of elevation is ${60}^{\circ }.$ How high above the ground is the kite?

Figure \(\PageIndex{29}\)

Answer

We can solve this using the sine function, $\sin \theta=\frac{o p p}{h y p}$.

$$\begin{aligned} \sin 60^{\circ} & =\frac{x}{50} \\ 50 \sin 60^{\circ} & =x \\ & =43.3 \mathrm{ft} \end{aligned} \nonumber$$
$$\begin{array}{c}\hfill \end{array}$$

Your Turn $\PageIndex{12}$

You are flying a kite on a 60-foot string. The angle of elevation from the ground to the kite is ${50^ \circ}$. How high above the ground is the kite?

Figure \(\PageIndex{30}\)

People in Mathematics: Pythagoras and the Pythagoreans

The Pythagorean Theorem is so widely used that most people assume that Pythagoras (570–490 BC) discovered it. The philosopher and mathematician uncovered evidence of the right triangle concepts in the teachings of the Babylonians dating around 1900 BC. However, it was Pythagoras who found countless applications of the theorem leading to advances in geometry, architecture, astronomy, and engineering.

Among his accolades, Pythagoras founded a school for the study of mathematics and music. Students were called the Pythagoreans, and the school’s teachings could be classified as a religious indoctrination just as much as an academic experience. Pythagoras believed that spirituality and science coexist, that the intellectual mind is superior to the senses, and that intuition should be honored over observation.

Pythagoras was convinced that the universe could be defined by numbers, and that the natural world was based on mathematics. His primary belief was All is Number. He even attributed certain qualities to certain numbers, such as the number 8 represented justice and the number 7 represented wisdom. There was a quasi-mythology that surrounded Pythagoras. His followers thought that he was more of a spiritual being, a sort of mystic that was all-knowing and could travel through time and space. Some believed that Pythagoras had mystical powers, although these beliefs were never substantiated.

Pythagoras and his followers contributed more ideas to the field of mathematics, music, and astronomy besides the Pythagorean Theorem. The Pythagoreans are credited with the discovery of irrational numbers and of proving that the morning star was the planet Venus and not a star at all. They are also credited with the discovery of the musical scale and that different strings made different sounds based on their length. Some other concepts attributed to the Pythagoreans include the properties relating to triangles other than the right triangle, one of which is that the sum of the interior angles of a triangle equals ${180}^{\circ }.$ These geometric principles, proposed by the Pythagoreans, were proven 200 years later by Euclid.

Who Knew?: A Visualization of the Pythagorean Theorem

In Figure 10.208, which is one of the more popular visualizations of the Pythagorean Theorem, we see that square $a$ is attached to side $a$; square $b$ is attached to side $b$; and the largest square, square $c$, is attached to side $c$. Side $a$ measures 3 cm in length, side $b$ measures 4 cm in length, and side $c$ measures 5 cm in length. By definition, the area of square $a$ measures 9 square units, the area of square $b$ measures 16 square units, and the area of square $c$ measures 25 square units. Substitute the values given for the areas of the three squares into the Pythagorean Theorem and we have

$$\begin{aligned} a^2+b^2 & =c^2 \\ 3^2+4^2 & =5^2 \\ 9+16 & =25 \end{aligned} \nonumber$$

Thus, the sum of the squares of the two legs of a right triangle is equal to the square of the hypotenuse, as stated in the Pythagorean Theorem.

Figure \(\PageIndex{31}\)

Check Your Understanding

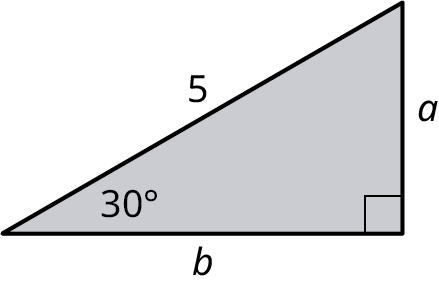
1. Find the lengths of the unknown sides of the ${30^ \circ } {\text{-}} {60^ \circ } {\text{-}} {90^ \circ }$ triangle shown..

2. Find the missing lengths of the ${45^ \circ } {\text{-}} {45^ \circ } {\text{-}} {90^ \circ }$ triangle shown.

3. Use the Pythagorean theorem to find the missing length in the triangle shown.

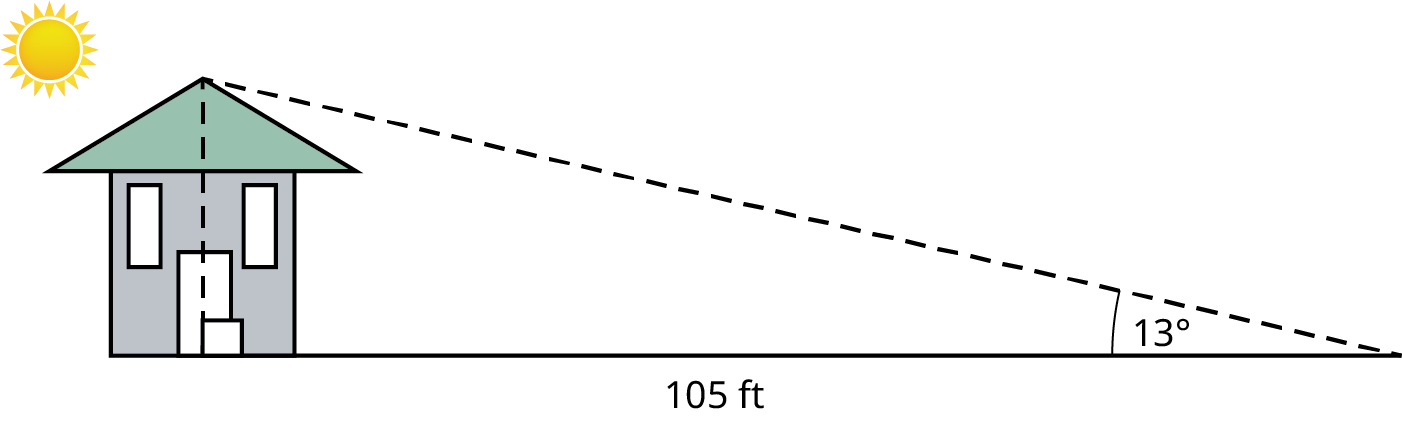
4. The sun casts a shadow over the roof of a house that ends 105 ft from the front door as shown in the figure. How high is the house to the tip of the roof?

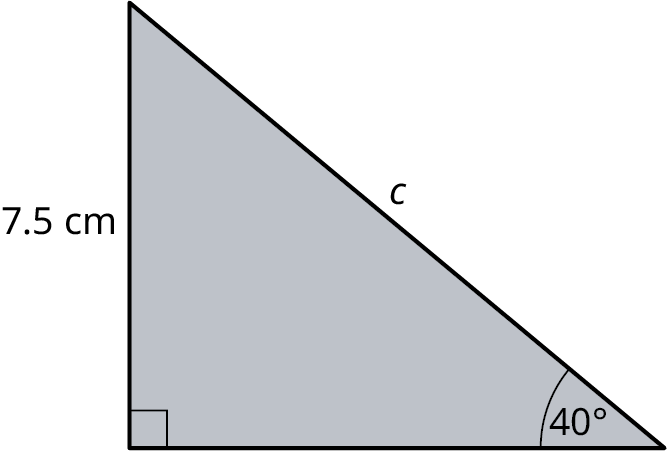
5. Find the measure of side $c$ in the given figure.

6. Find the measure of side $x$ in the given figure.