Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

15.11: Chapter 12

Last updated

Jan 2, 2025
Save as PDF
- 15.10: Chapter 11
- 15.12: Chapter 13

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Your Turn

12.1

1. The vertices are p, q, r, s, and t. The edges are pq, pr, pt, qr, qs, qt, rs, and st.

12.2

1. The pairs that are not adjacent are p and s, p and t, and r and t.

12.3

1. Vertex q

12.4

A graph represents common boundaries between regions of Oahu. The five vertices are L, N, W, C, and S. Edges connect L with N and C. Edges connect N with W and C. Edges connect W with C and S. An edge connects S with C. — Graph Representing Common Boundaries Between Regions of Oahu

12.5

1. The objects that are represented with vertices are poker players. An edge between a pair of vertices would indicate the two players competed against each other at table. This is best represented as a graph because players from the same table never meet a second time. Also, a player cannot compete against themself; so, there is no need for a loop.

12.6

1. Graph E, 34

2. Graph D, 18

3. higher

12.7

1. 3

2. Answers may vary. Two possible graphs are shown.
Graph 1:

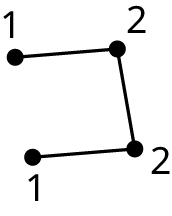
$One graph labeled graph 1. The graph has four vertices labeled 1, 2, 2, and 1. The edges connect 1 2, 2 2, and 2 1.$
Graph 2:

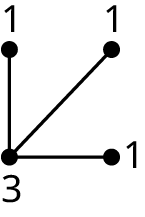
$One graph labeled graph 2. The graph has four vertices labeled 1, 3, 1, and 1. The edges connect 1 3, 3 1, and 3 1.$

12.8

1. 124,750 introductions

12.9

$Graph F has four vertices: V, W, X, and Z. The edges connect X W, X V, V W, X Z, and W Z.$

12.10

1. Triangle: (a, b, e or a, d, e)
Quadrilateral: (b, c, d, e or a, b, e, d)
Pentagon: (a, b, c, d, e)

12.11

1. (B, D, C, E, F)

12.12

1. 186

12.13

1. Graph C₁ has 6 edges, but Graph C₂ has 8.
Graph C₁ has 4 vertices and Graph C₂ has 5.
Graph C₁ has no vertex of degree 4, but Graph C₂ has one vertex of degree 4.
They do not have the same cycles. For example, Graph C₂ has a pentagon cycle, but Graph C₁ does not.

12.14

1. Answers may vary.

The total number of vertices in each graph is different. The Diamonds graph has 17 vertices while Dots graph has only 16.
The degrees of vertices differ. The Diamonds graph has vertices of degrees 4 while the Dots graph does not.
The graphs have different sizes of cyclic subgraphs. The Diamonds graph has 4 squares (4-cycles), while the Dots graph has 3 squares. Also, the Dots graph has 8-cycles while the Diamonds graph does not.

12.15

1. Answers may vary. There are four possible isomorphisms:

a − q, d − s, c − p, and b − r.
a − p, d − s, c − q, and b − r.
a − q, d − r, c − p, and b − s.
a − p, d − r, c − q, and b − s.

12.16

1. Caden is correct because Graph E could be untangled so that d is to the left of c and the edges bc and ad are no longer crossed. Maubi is incorrect because (a, b, c, d) is a quadrilateral in Graph E. Javier is incorrect because the portion of the graph he highlighted does not have 3 vertices and is not a triangle.

12.17

$The complement of graph H is displayed. The vertices are A, B, C, D, and E. The edges connect B E, B D, and E C.$

12.18

1. The degrees are 0. There are no adjacent vertices in Graph N since all vertices are adjacent in Graph M.

12.19

1. c Only C → V → G → B → B is a walk.

12.20

1. walk, path, and trail

2. walk and a trail, but not a path

3. none of these

12.21

1. To fly from Palm Beach to any other city, you must take the flight from PBI to TPA. To return, you must take the flight from TPA to PBI. This means that the graph of any itinerary that begins and ends at PBI covers the same edge twice and is not a circuit.

2. The degree of PBI is 1 meaning that there is only one edge connecting PBI to other parts of the graph.

12.22

1. Yes. The chromatic number is 4 or less.

2. 3

3. 3 or 4

4. Graphs 1 and 3

5. Answers may vary. Here is an example of a 3-coloring:

$A graph with seven vertices. It has 2 vertices in red, 3 vertices in blue, and 2 vertices in purple. Edges from the first red vertex lead to two blue vertices and two purple vertices. The first purple and the first blue vertices are connected by an edge. The second purple and the second blue vertices are connected by an edge. The second purple connects with the second red and third blue via edges. The second red and third blue are connected via an edge.$

12.23

1. The chromatic number is 3. Here is a 3-coloring of the graph:

$A graph represents common boundaries between regions of Oahu. The five vertices are L, N, W, C, and S. L and W are in purple. N and S are in blue. C is in red. Edges from L connect with N and C. Edges from N connect with W and C. Edges from W connect with C and S. An edge from S connects with S.$

12.24

1. Graphs G, H, and I are connected; so, they each have a single component with the vertices {a, b, c, d}. Graph F is disconnected with two components, {a, c, d} and {b}. Graph J is disconnected with two components, {a, d} and {b, c}. Graph K is disconnected with three components, {a}, {b, d}, and {c}.

12.25

1. Each pair of vertices would be connected by a path that was at most 6 edges long. So, the graph would be connected.

12.26

1. The multigraph of the neighborhood is shown:

$A graph of a neighborhood has 16 vertices arranged in 4 rows and 4 columns. The vertices are connected to form 9 squares. On each side, a curved edge connects the center two vertices.$

2. Yes, the graph is connected. It has only one component.

3. There are four corner vertices of degree 2 and the remaining twelve vertices are all degree 4.

4. Yes

5. Yes, an Eulerian graph has an Euler circuit; so, it is possible.

12.27

1. Graph X does not have an Euler circuit because it is disconnected.

2. a → b → g → d → f → c → g → e → a

12.28

$Graph Z has four vertices: a, b, c, and d. The edges connect a b, b d, d c, and c a. A double edge connects a to d.$

12.29

1. Yes.

2. No. It doesn’t cover every edge.

3. No. It is not a walk, because the vertices b and e are not adjacent.

12.30

1. In a complete graph with three or more vertices, any three vertices form a triangle which is a cycle. Any edge in a graph that is part of a cycle cannot be a bridge so, there are no bridges in a complete graph. Also, any edge that is part of a triangle cannot be a local bridge because the removal of any edge of a triangle will leave a path of only two edges between the vertices of that edge. So, there are no bridges or local bridges in a complete graph.

12.31

1. m

2. qn, qt; qn bridge

3. rs, st, tq, qn

4. nm, np; nm,, bridge

5. om, mp, pn, nm

6. s → q → r → s → t → q → n → o → m → p → n → m

12.32

1. The graph has Euler trails. They must begin and end at vertices u and v. An example is
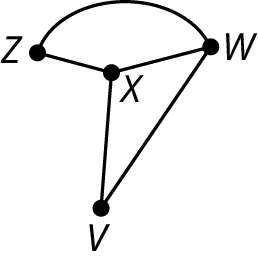
v → w → x → u → z → y → w → u

12.33

1. both

12.34

$n! = 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720$ and

$\left( {n - 1} \right)! = (6 - 1)! = 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120$

12.35

$5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120$

12.36

1. 120

12.37

1. 26

12.38

1. No

2. No

3. Yes

12.39

1. C → A → B → F → D → E

12.40

1. p → m → o → n → q → t → s → r

2. none

3. none

12.41

1. Hamilton path

2. Euler trail

3. neither

12.42

1. brute force algorithm

12.43

V → W → X → Y → Z → V
V → W → X → Z → Y → V
V → W → Y → X → Z → V
V → W → Y → Z → X → V
V → W → Z → X → Y → V
V → W → Z → Y → X → V
V → X → W → Y → Z → V
V → X → W → Z → Y → V
V → X → Y → W → Z → V
V → X → Y → Z → W → V (reverse of 6)
V → X → Z → W → Y → V
V → X → Z → Y → W → V (reverse of 4)
V → Y → X → W → Z → V
V → Y → X → Z → W → V (reverse of 5)
V → Y → W → X → Z → V
V → Y → W → Z → X → V (reverse of 11)
V → Y → Z → X → W → V (reverse of 2)
V → Y → Z → W → X → V (reverse of 8)
V → Z → X → Y → W → V (reverse of 3)
V → Z → X → W → Y → V (reverse of 15)
V → Z → Y → X → W → V (reverse of 1)
V → Z → Y → W → X → V (reverse of 7)
V → Z → W → X → Y → V (reverse of 13)
V → Z → W → Y → X → V (reverse of 9)

12.44

1. The officer should travel from Travis Air Force Base to Beal Air Force Base, to Edwards Air Force Base, to Los Angeles Air Force Base, and return to Travis.

12.45

1. D → B → E → A → C → F → D; 550 min or 9 hrs 10 min.

12.46

1. The star topology is a tree, and the tree topology is a tree. The ring topology and the mesh topology are not trees because they contain cycles.

12.47

1. star topology

2. tree topology

3. none

12.48

1. Vertices k, l, and m are in one component, and vertices g, h, i, and j are in the other.

2. There are 6 vertices and 5 edges, which confirms Graph I is a tree, because the number of edges is one less than the number of vertices.

3. a quadrilateral

12.49

1. a True

2. b False

3. a True

4. a True

12.50

1. Answers may vary. Here are three possible spanning trees of Graph J:

$Three graphs. Each graph has 6 vertices and 5 edges.$

12.51

1. The three edges must include one edge from list A and one pair of edges from list B.
List A: be, eh, hi, gi, bg
List B: ac and ad, ac and af, ac and cd, ac and cf, ad and af, ad and cd, ad and cf, af and cd, af and cf, or cd and cf.

12.52

1. There are two possible minimum spanning trees, each with a total weight of 174:

$Two weighted graphs. The vertices in each graph are as follows: U, V, W, X, and Y. The edges in the first graph are as follows. U W, 37. W X, 45. W V, 68. V Y, 24. The edges in the second graph are as follows. U W, 37. W X, 45. X Y, 68. Y V, 24.$

Check Your Understanding

1. a True

2. b False

3. a True

4. b False

5. b False

6. b False

7. a True

8. b False

9. a True

10. b

11. a True

12. The sum of the degrees is always double the number of edges, which means it has to be an even number, but 13 is odd.

13. Yes. If n is the number of vertices in a complete graph, the number of edges is \(\frac

UndefinedNameError: reference to undefined name 'n' (click for details)

Callstack:
    at (Bookshelves/Applied_Mathematics/Contemporary_Mathematics_(OpenStax)/15:_Answer_Key/15.11:_Chapter_12), /content/body/div/div/div[53]/div/div[13]/span, line 1, column 1

{2} = \frac{n}{2}(n - 1)\) which is half the number of vertices times one less than the number of vertices.

14. always true

15. never true

16. sometimes true

17. never true

18. always true

19. sometimes true

20. sometimes true

21. never true

22. sometimes true

23. always true

24. always true

25. sometimes true

26. always true

27. sometimes true

28. always true

29. always true

30. sometimes true

31. always true

32. sometimes true

33. always true

34. always true

35. has no repeated egdes

36. is closed

37. has no repeated vertices

38. has no repeated edges

39.

$n$

40. at least

51. edge

52. Fleury’s

53. circuit, trail

54. components

55. local bridge

56. bridge

57. vertex

58. complete

59. is

60. is

61. is not

62. is

63. is

64. is not

65. is not

66. is not

67. different from

68. the same as

69. different from

70. different from

71. b False

72. b False

73. b False

74. a True

75. a True

76. b False

77. b False

78. b False

79. a True

80. b False

81. b False

82. a True

83. a True

84. b False

85. b False

86. a True

87. a True

88. a True

89. a True

90. b False

91. b False

92. a True

93. a True

94. a True

Your Turn

Check Your Understanding

Support Center

How can we help?