4.1.1: Simplifying Ratios and Rates

Learning Objectives

• Write ratios and rates as fractions in simplest form.
• Find unit rates.
• Find unit prices.

Introduction

Ratios are used to compare amounts or quantities or describe a relationship between two amounts or quantities. For example, a ratio might be used to describe the cost of a month’s rent as compared to the income earned in one month. You may also use a ratio to compare the number of elephants to the total number of animals in a zoo, or the amount of calories per serving in two different brands of ice cream.

Rates are a special type of ratio used to describe a relationship between different units of measure, such as speed, wages, or prices. A car can be described as traveling 60 miles per hour; a landscaper might earn $35 per lawn mowed; gas may be sold at $3 per gallon.

Ratios

Ratios compare quantities using division. This means that you can set up a ratio between two quantities as a division expression between those same two quantities.

Here is an example. If you have a platter containing 10 sugar cookies and 20 chocolate chip cookies, you can compare the cookies using a ratio.

The ratio of sugar cookies to chocolate chip cookies is:

\(\ \frac{\text { sugar cookies }}{\text { chocolate chip cookies }}=\frac{10}{20}\)

The ratio of chocolate chip cookies to sugar cookies is:

\(\ \frac{\text { chocolate chip cookies }}{\text { sugar cookies }}=\frac{20}{10}\)

You can write the ratio using words, a fraction, and also using a colon as shown below.

\(\ \begin{array}{c}
\text { ratio of } {\color{red}\text{sugar cookies to}}\\
\color{blue}\text{chocolate chip cookies}\\
{\color{red} 10} \text{ to } \color{blue}20\\
\frac{\color{red}10}{\color{blue}20}\\
{\color{red}10}:\color{blue}20
\end{array}\)

Some people think about this ratio as: “For every 10 sugar cookies I have, I have 20 chocolate chip cookies.”

You can also simplify the ratio just as you simplify a fraction.

\(\ \frac{10}{20}=\frac{10 \div 10}{20 \div 10}=\frac{1}{2}\)

So we can also say that:

\(\ \begin{array}{c}
\text { ratio of } {\color{red}\text{sugar cookies to}}\\
\color{blue}\text{chocolate chip cookies}\\
{\color{red} 1} \text{ to } \color{blue}2\\
\frac{\color{red}1}{\color{blue}2}\\
{\color{red}1}:\color{blue}2
\end{array}\)

How to Write a Ratio

A ratio can be written in three different ways:

• with the word “to”: 3 to 4
• as a fraction: \(\ \frac{3}{4}\)
• with a colon: 3:4

A ratio is simplified if it is equivalent to a fraction that has been simplified.

Below are two more examples that illustrate how to compare quantities using a ratio, and how to express the ratio in simplified form.

Example

A basketball player takes 50 jump shots during a practice. She makes 28 of them. What is the ratio of shots made to shots taken? Simplify the ratio.

Solution

\(\ \frac{\text { shots made }}{\text { shots taken }}\)	Identify the relationship.
\(\ \frac{28}{50}\)	Express the two quantities in fraction form.
\(\ \frac{28 \div 2}{50 \div 2}=\frac{14}{25}\)	Simplify the fraction to express the ratio in simplest form.
\(\ \begin{array}{r} 14: 25 \\ 14 \text { to } 25 \end{array}\)	Consider the two other ways to write a ratio. You’ll want to express your answer in a particular format if required.

The ratio of shots made to shots taken is \(\ \frac{14}{25}\), 14:15, or 14 to 15.

Often, one quantity in the ratio is greater than the second quantity. You do not have to write the ratio so that the lesser quantity comes first; the important thing is to keep the relationship consistent.

Example

Paul is comparing the amount of calories in a large order of French fries from his two favorite fast food restaurants. Fast Foodz advertises that an order of fries has 450 calories, and Beef Stop states that its fries have 300 calories. Write a ratio that represents the amount of calories in the Fast Foodz fries compared to the calories in Beef Stop fries.

Solution

\(\ \frac{\text { calories in Fast Foodz fries }}{\text { calories in Beef Stop fries }}\)	Identify the relationship.
\(\ \frac{450}{300}\)	Write a ratio comparing calories.
\(\ \frac{450 \div 150}{300 \div 150}=\frac{3}{2}\)	Simplify the ratio. 450 and 300 have a common factor of 150.

The ratio of calories in Fast Foodz fries to Beef Stop fries is \frac{3}{2}, 3:2, or 3 to 2.

Ratios can compare a part to a part or a part to a whole. Consider the example below that describes guests at a party.

Example

Luisa invites a group of friends to a party. Including Luisa, there are a total of 22 people, 10 of whom are women.

Which is greater: the ratio of women to men at the party, or the ratio of women to the total number of people present?

Solution

\(\ \frac{\text { number of women }}{\text { number of men }}\)	Identify the first relationship.
\(\ \frac{10}{12}\)	Write a ratio comparing women to men. Since there are 22 people and 10 are women, 12 must be men.
\(\ \frac{10 \div 2}{12 \div 2}=\frac{5}{6}\)	Simplify the ratio. 10 and 12 have a common factor of 2; the ratio of women to men at the party is \(\ \frac{5}{6}\).
\(\ \frac{\text { number of women }}{\text { number of people }}\)	Identify the next relationship.
\(\ \frac{10}{22}\)	Write a ratio comparing the number of women to the total number of people at the party.
\(\ \frac{10 \div 2}{22 \div 2}=\frac{5}{11}\)	Simplify the ratio. 10 and 22 have a common factor of 2.
\(\ \begin{array}{l} \frac{5 \cdot 11}{6 \cdot 11}=\frac{55}{66} \\ \frac{5 \cdot 6}{11 \cdot 6}=\frac{30}{66} \end{array}\)	Rewrite each fraction with a common denominator, 66.
\(\ \frac{5}{6}>\frac{5}{11}\)	Since \(\ \frac{55}{66}>\frac{30}{66}\).

The ratio of women to men at the party, \(\ \frac{5}{6}\), is greater than the ratio of women to the total number of people, \(\ \frac{5}{11}\).

Exercise

A poll at Forrester University found that 4,000 out of 6,000 students are unmarried. Find the ratio of unmarried to married students. Express as a simplified ratio.

1. 3 to 2
2. 1 to 3
3. 2 to 1
4. 2 to 3

Answer

1. Incorrect. The ratio 3 to 2 compares the total number of students to the number of unmarried students. The correct answer is 2 to 1.
2. Incorrect. The ratio 1 to 3 compares the number of married students to the total number of students. The correct answer is 2 to 1.
3. Correct. If 4,000 students out of 6,000 are unmarried, then 2,000 must be married. The ratio of unmarried to married students can be represented as 4,000 to 2,000, or simply 2 to 1.
4. Incorrect. The ratio 2 to 3 compares the number of unmarried students to the total number of students. The correct answer is 2 to 1.

Rates

A rate is a ratio that compares two different quantities that have different units of measure. A rate is a comparison that provides information such as dollars per hour, feet per second, miles per hour, and dollars per quart, for example. The word “per” usually indicates you are dealing with a rate. Rates can be written using words, using a colon, or as a fraction. It is important that you know which quantities are being compared.

For example, an employer wants to rent 6 buses to transport a group of 300 people on a company outing. The rate to describe the relationship can be written using words, using a colon, or as a fraction; and you must include the units.

\(\ \begin{array}{c}
\text{six buses per }300 \text{ people}\\
6 \text{ buses : }300 \text{ people}\\
\frac{6 \text{ buses}}{300 \text{ people}}
\end{array}\)

As with ratios, this rate can be expressed in simplest form by simplifying the fraction.

\(\ \frac{6 \text { buses}{\div6 }}{300 \text { people}{\div6 }}=\frac{1 \text { bus }}{50 \text { people }}\)

This fraction means that the rate of buses to people is 6 to 300 or, simplified, 1 bus for every 50 people.

Example

Write the rate as a simplified fraction: 8 phone lines for 36 employees.

Solution

\(\ \frac{8 \text { phone lines }}{36 \text { employees }}\)	Write as a fraction.
\(\ \frac{8 \text { phone lines}{\div4 }}{36 \text { employees}{\div4 }}=\frac{2 \text { phone lines }}{9 \text { employees }}\)	Simplify the fraction by using the common factor of 4.

The rate of phone lines for employees can be expressed as \(\ \frac{2 \text { phone lines }}{9 \text { employees }}\).

Example

Write the rate as a simplified fraction: 6 flight attendants for 200 passengers.

Solution

\(\ \frac{6 \text { flight attendants }}{200 \text { passengers }}\)	Write as a fraction.
\(\ \frac{6 \text { flight attendants}{\div2 }}{200 \text { passengers}\div2}=\frac{3 \text { flight attendants }}{100 \text { passengers }}\)	Simplify the fraction by using the common factor of 2.

The rate of flight attendants to passengers is \(\ \frac{3 \text { flight attendants }}{100 \text { passengers }}\).

Exercise

Anyla rides her bike 18 blocks in 20 minutes. Express her rate as a simplified fraction.

1. \(\ 18: 20\)
2. \(\ \begin{array}{cc}
   9 & \text { blocks } \\
   \hline 10 & \text { minutes }
   \end{array}\)
3. \(\ \frac{9 \text { minutes }}{10 \text { blocks }}\)
4. \(\ \frac{18 \text { blocks }}{20 \text { minutes }}\)

Answer

1. \(\ 18: 20\)

   Incorrect. Anyla’s trip compares quantities with different units, so it can be described as a rate. Since rates compare two quantities measured in different units of measurement, they must include their units. The correct answer is \(\ \begin{aligned}
   9 & \text { blocks } \\
   \hline 10 & \text { minutes }
   \end{aligned}\).

2. \(\ \begin{array}{cc}
   9 & \text { blocks } \\
   \hline 10 & \text { minutes }
   \end{array}\)

   Correct. Anyla’s trip compares quantities with different units (blocks and minutes), so it is a rate and can be written \(\ \begin{array}{cc}
   18 & \text { blocks } \\
   \hline 20 & \text { minutes }
   \end{array}\). This fraction can be simplified by dividing both the numerator and the denominator by 2.

3. \(\ \frac{9 \text { minutes }}{10 \text { blocks }}\)

   Incorrect. 18 blocks in 20 minutes is not equivalent to 10 blocks in 9 minutes. Check the units again in your answer. The correct answer is \(\ \begin{aligned}
   9 & \text { blocks } \\
   \hline 10 & \text { minutes }
   \end{aligned}\).

4. \(\ \frac{18 \text { blocks }}{20 \text { minutes }}\)

   Incorrect. Anyla’s trip compares quantities with different units, so it can be described as a rate. This is a correct representation and includes the units, but the fraction can be simplified. The correct answer is \(\ \begin{aligned}
   9 & \text { blocks } \\
   \hline 10 & \text { minutes }
   \end{aligned}\).

Finding Unit Rates

A unit rate compares a quantity to one unit of measure. You often see the speed at which an object is traveling in terms of its unit rate.

For example, if you wanted to describe the speed of a boy riding his bike—and you had the measurement of the distance he traveled in miles in 2 hours—you would most likely express the speed by describing the distance traveled in one hour. This is a unit rate; it gives the distance traveled per one hour. The denominator of a unit rate will always be one.

Consider the example of a car that travels 300 miles in 5 hours. To find the unit rate, you find the number of miles traveled in one hour.

\(\ \frac{300 \text { miles}{\div5 }}{5 \text { hours}{\div5 }}=\frac{60 \text { miles }}{1 \text { hour }}\)

A common way to write this unit rate is 60 miles per hour.

Example

A crowded subway train has 375 passengers distributed evenly among 5 cars. What is the unit rate of passengers per subway car?

Solution

\(\ \frac{\text { passengers }}{\text { subway cars }}\)	Identify the relationship.
\(\ \frac{375 \text { passengers }}{5 \text { subway cars }}\)	Write the rate as a fraction.
\(\ \frac{375 \text { passengers } \div 5}{5 \text { subway cars } \div 5}=\frac{75 \text { passengers }}{1 \text { subway car }}\)	Express the fraction with 1 in the denominator to find the number of passengers in one subway car.

The unit rate of the subway car is 75 riders per subway car.

Finding Unit Prices

A unit price is a unit rate that expresses the price of something. The unit price always describes the price of one unit, so that you can easily compare prices.

You may have noticed that grocery shelves are marked with the unit price (as well as the total price) of each product. This unit price makes it easy for shoppers to compare the prices of competing brands and different package sizes.

Consider the two containers of blueberries shown below. It might be difficult to decide which is the better buy just by looking at the prices; the container on the left is cheaper, but you also get fewer blueberries. A better indicator of value is the price per single ounce of blueberries for each container.

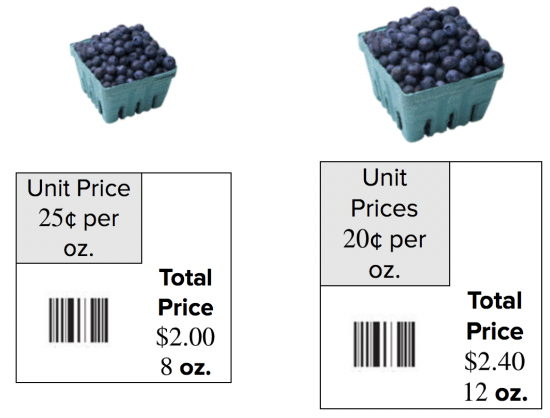
Look at the unit prices—the container on the right is actually a better deal, since the price per ounce is lower than the unit price of the container on the left. You pay more money for the larger container of blueberries, but you also get more blueberries than you would with the smaller container. Put simply, the container on the right is a better value than the container on the left.

So, how do you find the unit price?

Imagine a shopper wanted to use unit prices to compare a 3-pack of tissue for $4.98 to a single box of tissue priced at $1.60. Which is the better deal?

Find the unit price of the 3-pack: \(\ \frac{\$ 4.98}{3 \text { boxes }}\)

Since the price given is for 3 boxes, divide both the numerator and the denominator by 3 to get the price of 1 box, the unit price. The unit price is $1.66 per box.

The unit price of the 3-pack is $1.66 per box; compare this to the price of a single box at $1.60. Surprisingly, the 3-pack has a higher unit price! Purchasing the single box is the better value.

Like rates, unit prices are often described with the word “per.” Sometimes, a slanted line / is used to mean “per.” The price of the tissue might be written $1.60/box, which is read "$1.60 per box."

Example

3 pounds of sirloin tips cost $21. What is the unit price per pound?

Solution

\(\ \frac{\$ 21.00}{3 \text { pounds }}\)	Write a rate to represent the cost per number of pounds.
\(\ \frac{\$ 21.00 \div 3}{3 \text { pounds}{\div3 }}=\frac{\$ 7.00}{1 \text { pound }}\)	Express the fraction with 1 in the denominator by dividing both the numerator and the denominator by 3.

The unit price of the sirloin tips is $7.00/pound.

The following example shows how to use unit price to compare two products and determine which has the lower price.

Example

Sami is trying to decide between two brands of crackers. Which brand has the lower unit price?

Brand A: $1.12 for 8 ounces

Brand B: $1.56 for 12 ounces

Solution

Brand A
\(\ \frac{\$ 1.12}{8 \text { ounces }}\)	Write a rate to represent the cost per ounce for Brand A.
\(\ \frac{\$ 1.12 \div 8}{8 \text { ounces}{\div8 }}=\frac{\$ 0.14}{1 \text { ounce }}\)	Find the unit price of Brand A by dividing both the numerator and the denominator by 8.
Brand B
\(\ \frac{\$ 1.56}{12 \text { ounces }}\)	Write a rate to represent the cost per ounce for Brand B.
\(\ \frac{\$ 1.56 \div 12}{12 \text { ounces }{\div12 }}=\frac{\$ 0.13}{1 \text { ounce }}\)	Find the unit price of Brand B by dividing both the numerator and the denominator by 12.
\(\ \frac{\$ 0.14}{1 \text { ounce }}>\frac{\$ 0.13}{1 \text { ounce }}\)	Compare unit prices.

The unit price of Brand A crackers is 14 cents/ounce and the unit price of Brand B is 13 cents/ounce. Brand B has a lower unit price and represents the better value.

Exercise

A shopper is comparing two packages of rice at the grocery store. A 10-pound package costs $9.89 and a 2-pound package costs $1.90. Which package has the lower unit price to the nearest cent? What is its unit price?

1. The 2-pound bag has a lower unit price of $.95/pound.
2. The 10-pound bag has a lower unit price of $0.99/pound.
3. The 10-pound bag has a lower unit price of $.95/pound.
4. The 2-pound bag has a lower price of $1.89/2pound.

Answer

1. Correct. The unit price per pound for the 2-pound bag is \(\ \$ 1.90 \div 2=\$ 0.95\). The unit price per pound for the 10-pound bag is \(\ \$ 9.89 \div 10=\$ 0.989\), which rounds to $0.99.
2. Incorrect. \(\ \$ 9.89 \div 10=\$ 0.989\), which rounds to $0.99. \(\ \$ 1.90 \div 2=\$ 0.95\). The 2-pound bag has a lower unit price. The correct answer is A.
3. Incorrect. \(\ \$ 9.89 \div 10=\$ 0.989\), which rounds to $0.99. The correct answer is A.
4. Incorrect. A unit price is the price for one unit; in this case, you need to find the cost of one pound, not two pounds. The correct answer is A.

Summary

Ratios and rates are used to compare quantities and express relationships between quantities measured in the same units of measure and in different units of measure. They both can be written as a fraction, using a colon, or using the words “to” or “per”. Since rates compare two quantities measured in different units of measurement, such as dollars per hour or sick days per year, they must include their units. A unit rate or unit price is a rate that describes the rate or price for one unit of measure.