4.2.1: Understanding Proportions

Last updated
Save as PDF

Page ID: 62073

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Determine whether a proportion is true or false.
Find an unknown in a proportion.
Solve application problems using proportions.

Introduction

A true proportion is an equation that states that two ratios are equal. If you know one ratio in a proportion, you can use that information to find values in the other equivalent ratio. Using proportions can help you solve problems such as increasing a recipe to feed a larger crowd of people, creating a design with certain consistent features, or enlarging or reducing an image to scale.

For example, imagine you want to enlarge a 5-inch by 8-inch photograph to fit a wood frame that you purchased. If you want the shorter edge of the enlarged photo to measure 10 inches, how long does the photo have to be for the image to scale correctly? You can set up a proportion to determine the length of the enlarged photo.

Determining Whether a Proportion is True or False

A proportion is usually written as two equivalent fractions. For example:

$\ \frac{12 \text { inches }}{1 \text { foot }}=\frac{36 \text { inches }}{3 \text { feet }}$

Notice that the equation has a ratio on each side of the equal sign. Each ratio compares the same units, inches and feet, and the ratios are equivalent because the units are consistent, and $\ \frac{12}{1}$ is equivalent to $\ \frac{36}{3}$.

Proportions might also compare two ratios with the same units. For example, Juanita has two different-sized containers of lemonade mix. She wants to compare them. She could set up a proportion to compare the number of ounces in each container to the number of servings of lemonade that can be made from each container.

$\ \frac{40 \text { ounces }}{84 \text { ounces }}=\frac{10 \text { servings }}{21 \text { servings }}$

Since the units for each ratio are the same, you can express the proportion without the units:

$\ \frac{40}{84}=\frac{10}{21}$

When using this type of proportion, it is important that the numerators represent the same situation. In the example above they represent 40 ounces for 10 servings. The denominators should also represent the same situation, which is ounces for servings.

Juanita could also have set up the proportion to compare the ratios of the container sizes to the number of servings of each container.

$\ \frac{40 \text { ounces }}{10 \text { servings }}=\frac{84 \text { ounces }}{21 \text { servings }}$

Sometimes you will need to figure out whether two ratios are, in fact, a true or false proportion. Below is an example that shows the steps of determining whether a proportion is true or false.

Example

Is the proportion true or false?

$\ \frac{100 \text { miles }}{4 \text { gallons }}=\frac{50 \text { miles }}{2 \text { gallons }}$

Solution

miles (check)

The units are consistent across the numerators.

gallons (check)

The units are consistent across the denominators.

Write each ratio in simplest form.

$\ \begin{array}{l}
\frac{100 \div 4}{4 \div 4}=\frac{25}{1} \\
\frac{50 \div 2}{2 \div 2}=\frac{25}{1} \\
\frac{25}{1}=\frac{25}{1}
\end{array}$

Since the simplified fractions are equivalent, the proportion is true.

The proportion is true.

Identifying True Proportions

To determine if a proportion compares equal ratios or not, you can follow these steps.

Check to make sure that the units in the individual ratios are consistent either vertically or horizontally. For example, $\ \frac{\text { miles }}{\text { hour }}=\frac{\text { miles }}{\text { hour }}$ or $\ \frac{\text { miles }}{\text { miles }}=\frac{\text { hour }}{\text { hour }}$ are valid setups for a proportion.
Express each ratio as a simplified fraction.
If the simplified fractions are the same, the proportion is true; if the fractions are different, the proportion is false.

Sometimes you need to create a proportion before determining whether it is true or not. An example is shown below.

Example

One office has 3 printers for 18 computers. Another office has 20 printers for 105 computers. Is the ratio of printers to computers the same in these two offices?

Solution

$\ \frac{\text { printers }}{\text { computers }}=\frac{\text { printers }}{\text { computers }}$	Identify the relationship.
$\ \frac{3 \text { printers }}{18 \text { computers }}=\frac{20 \text { printers }}{105 \text { computers }}$	Write ratios that describe each situation, and set them equal to each other.
Printers (check)	Check that the units in the numerators match.
Computers (check)	Check that the units in the denominators match. Simplify each fraction and determine if they are equivalent.
$\ \begin{array}{c} \frac{3 \div 3}{18 \div 3}=\frac{1}{6} \\ \frac{20 \div 5}{105 \div 5}=\frac{4}{21} \\ \frac{1}{6} \neq \frac{4}{21} \end{array}$	Since the simplified fractions are not equal (designated by the $\ \neq$ sign), the proportion is not true.

The ratio of printers to computers is not the same in these two offices.

There is another way to determine whether a proportion is true or false. This method is called “finding the cross product” or “cross multiplying.”

To cross multiply, you multiply the numerator of the first ratio in the proportion by the denominator of the other ratio. Then multiply the denominator of the first ratio by the numerator of the second ratio in the proportion. If these products are equal, the proportion is true; if these products are not equal, the proportion is not true.

This strategy for determining whether a proportion is true is called cross-multiplying because the pattern of the multiplication looks like an “x” or a criss-cross. Below is an example of finding a cross product, or cross multiplying.

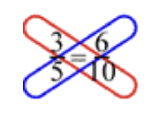
$Screen Shot 2021-04-29 at 3.54.27 PM.png$

In this example, you multiply $\ 3 \cdot 10=30$, and then multiply $\ 5 \cdot 6=30$. Both products are equal, so the proportion is true.

Below is another example of determining if a proportion is true or false by using cross products.

Example

Is the proportion true or false?

$\ \frac{5}{6}=\frac{9}{8}$

Solution

$Screen Shot 2021-04-29 at 3.png$	Identify the cross product relationship.
$\ \begin{array}{l} 5 \cdot 8=40 \\ 6 \cdot 9=54 \end{array}$	Use cross products to determine if the proportion is true or false.
$\ 40 \neq 54$	Since the products are not equal, the proportion is false.

The proportion is false.

Exercise

Is the proportion $\ \frac{3}{5}=\frac{24}{40}$ true or false?

True
False

Answer

Correct. Using cross products, you find that $\ 3 \cdot 40=120$ and $\ 5 \cdot 24=120$, so the cross products are equal and the proportion is true.
Incorrect. The cross products are equal, so the proportion is true. The correct answer is true.

Finding an Unknown Quantity in a Proportion

If you know that the relationship between quantities is proportional, you can use proportions to find missing quantities. Below is an example.

Example

Solve for the unknown quantity, $\ n$.

$\ \frac{n}{4}=\frac{25}{20}$

Solution

$\ 20 \cdot n=4 \cdot 25$	Cross multiply.
$\ 20 n=100$	You are looking for a number that when you multiply it by 20 you get 100.
$\ \begin{array}{r} 5\ \\ 20\longdiv{100} \end{array}$	You can find this value by dividing 100 by 20.

$\ n=5$

Now back to the original example. Imagine you want to enlarge a 5-inch by 8-inch photograph to make the length 10 inches and keep the proportion of the width to length the same. You can set up a proportion to determine the width of the enlarged photo.

$Screen Shot 2021-04-29 at 10.39.23 PM.png$

Example

Find the length of a photograph whose width is 10 inches and whose proportions are the same as a 5-inch by 8-inch photograph.

Solution

$\ \frac{\text { width }}{\text { length }}$	Determine the relationship.
Original photo: $\ \frac{5 \text { inches wide }}{8 \text { inches long }}$ Enlarged photo: $\ \frac{10 \text { inches wide }}{n \text { inches long }}$	Write a ratio that compares the length to the width of each photograph. Use a letter to represent the quantity that is not known (the width of the enlarged photo).
$\ \frac{5}{8}=\frac{10}{n}$	Write a proportion that states that the two ratios are equal.
$\ 5 \cdot n=8 \cdot 10$	Cross multiply.
$\ 5 n=80$	You are looking for a number that, when it is multiplied by 5, will give you 80.
$\ \begin{array}{l} \frac{5 n}{5}=\frac{80}{5} \\ n=\frac{80}{5} \end{array}$	Divide both sides by 5 to isolate the variable.
$\ n=16$	$\ \begin{array}{r} 16\ \\ 5\longdiv{80} \end{array}$

The length of the enlarged photograph is 16 inches.

Solving Application Problems Using Proportions

Setting up and solving a proportion is a helpful strategy for solving a variety of proportional reasoning problems. In these problems, it is always important to determine what the unknown value is, and then identify a proportional relationship that you can use to solve for the unknown value. Below are some examples.

Example

Among a species of tropical birds, 30 out of every 50 birds are female. If a certain bird sanctuary has a population of 1,150 of these birds, how many of them would you expect to be female?

Solution

Let $\ x$=the number of female birds in the sanctuary.	Determine the unknown item: the number of female birds in the sanctuary. Assign a letter to this unknown quantity.
$\ \frac{30 \text { female birds }}{50 \text { birds }}=\frac{x \text { female birds in sanctuary }}{1,150 \text { birds in sanctuary }}$	Set up a proportion, setting the ratios equal.
$\ \frac{30 \div 10}{50 \div 10}=\frac{3}{5}$ $\ \frac{3}{5}=\frac{x}{1150}$	Simplify the ratio on the left to make the upcoming cross multiplication easier.
$\ \begin{aligned} 3 \cdot 1150 &=5 \cdot x \\ 3,450 &=5 x \end{aligned}$	Cross multiply.
$\ \begin{array}{r} 690\ \\ 5\longdiv{3,450} \end{array}$	What number, when multiplied by 5, gives a product of 3,450? You can find this value by dividing 3,450 by 5.
$\ x=690$ birds

You would expect 690 birds in the sanctuary to be female.

Example

It takes Sandra 1 hour to word process 4 pages. At this rate, how long will she take to complete 27 pages?

Solution

$\ \frac{4 \text { pages }}{1 \text { hour }}=\frac{27 \text { pages }}{x \text { hours }}$	Set up a proportion comparing the pages she types and the time it takes to type them.
$\ 4 \cdot x=1 \cdot 27$	Cross multiply.
$\ 4 x=27$	You are looking for a number that, when it is multiplied by 4, will give you 27.
$\ \begin{array}{r} 6.75\ \\ 4\longdiv{27.00} \end{array}$	You can find this value by dividing 27 by 4.
$\ x=6.75 \text { hours }$

It will take Sandra 6.75 hours to complete 27 pages.

Exercise

A map uses a scale where 2 inches represents 5 miles. If the distance between two cities is shown on a map as 20 inches, how many miles apart are the two cities?

50 inches
50 miles
8 miles
100 miles

Answer

Incorrect. The distance between the cities is measured in inches on the map, but in miles in actuality. The correct answer is 50 miles.
Correct. Setting up the proportion $\ \frac{2 \text { inches }}{5 \text { miles }}=\frac{20 \text { inches }}{x}$, you find that $\ x=50$ miles.
Incorrect. When you solve a proportion, you cross multiply: $\ \frac{2 \text { inches }}{5 \text { miles }}=\frac{20 \text { inches }}{x}$, $\ 2 x=5 \cdot 20$. The correct answer is 50 miles.
Incorrect. When you solve a proportion, you cross multiply: $\ \frac{2 \text { inches }}{5 \text { miles }}=\frac{20 \text { inches }}{x}$, $\ 2 x=5 \cdot 20$. The correct answer is 50 miles.

Summary

A proportion is an equation comparing two ratios. If the ratios are equivalent, the proportion is true. If not, the proportion is false. Finding a cross product is another method for determining whether a proportion is true or false. Cross multiplying is also helpful for finding an unknown quantity in a proportional relationship. Setting up and solving proportions is a skill that is useful for solving a variety of problems.

\(\ \frac{\text { width }}{\text { length }}\)	Determine the relationship.
Original photo: \(\ \frac{5 \text { inches wide }}{8 \text { inches long }}\) Enlarged photo: \(\ \frac{10 \text { inches wide }}{n \text { inches long }}\)	Write a ratio that compares the length to the width of each photograph. Use a letter to represent the quantity that is not known (the width of the enlarged photo).
\(\ \frac{5}{8}=\frac{10}{n}\)	Write a proportion that states that the two ratios are equal.
\(\ 5 \cdot n=8 \cdot 10\)	Cross multiply.
\(\ 5 n=80\)	You are looking for a number that, when it is multiplied by 5, will give you 80.
\(\ \begin{array}{l} \frac{5 n}{5}=\frac{80}{5} \\ n=\frac{80}{5} \end{array}\)	Divide both sides by 5 to isolate the variable.
\(\ n=16\)	\(\ \begin{array}{r} 16\ \\ 5\longdiv{80} \end{array}\)

Let \(\ x\)=the number of female birds in the sanctuary.	Determine the unknown item: the number of female birds in the sanctuary. Assign a letter to this unknown quantity.
\(\ \frac{30 \text { female birds }}{50 \text { birds }}=\frac{x \text { female birds in sanctuary }}{1,150 \text { birds in sanctuary }}\)	Set up a proportion, setting the ratios equal.
\(\ \frac{30 \div 10}{50 \div 10}=\frac{3}{5}\) \(\ \frac{3}{5}=\frac{x}{1150}\)	Simplify the ratio on the left to make the upcoming cross multiplication easier.
\(\ \begin{aligned} 3 \cdot 1150 &=5 \cdot x \\ 3,450 &=5 x \end{aligned}\)	Cross multiply.
\(\ \begin{array}{r} 690\ \\ 5\longdiv{3,450} \end{array}\)	What number, when multiplied by 5, gives a product of 3,450? You can find this value by dividing 3,450 by 5.
\(\ x=690\) birds

\(\ \frac{4 \text { pages }}{1 \text { hour }}=\frac{27 \text { pages }}{x \text { hours }}\)	Set up a proportion comparing the pages she types and the time it takes to type them.
\(\ 4 \cdot x=1 \cdot 27\)	Cross multiply.
\(\ 4 x=27\)	You are looking for a number that, when it is multiplied by 4, will give you 27.
\(\ \begin{array}{r} 6.75\ \\ 4\longdiv{27.00} \end{array}\)	You can find this value by dividing 27 by 4.
\(\ x=6.75 \text { hours }\)

\(\ \frac{\text { printers }}{\text { computers }}=\frac{\text { printers }}{\text { computers }}\)	Identify the relationship.
\(\ \frac{3 \text { printers }}{18 \text { computers }}=\frac{20 \text { printers }}{105 \text { computers }}\)	Write ratios that describe each situation, and set them equal to each other.
Printers (check)	Check that the units in the numerators match.
Computers (check)	Check that the units in the denominators match. Simplify each fraction and determine if they are equivalent.
\(\ \begin{array}{c} \frac{3 \div 3}{18 \div 3}=\frac{1}{6} \\ \frac{20 \div 5}{105 \div 5}=\frac{4}{21} \\ \frac{1}{6} \neq \frac{4}{21} \end{array}\)	Since the simplified fractions are not equal (designated by the \(\ \neq\) sign), the proportion is not true.

$Screen Shot 2021-04-29 at 3.png$	Identify the cross product relationship.
\(\ \begin{array}{l} 5 \cdot 8=40 \\ 6 \cdot 9=54 \end{array}\)	Use cross products to determine if the proportion is true or false.
\(\ 40 \neq 54\)	Since the products are not equal, the proportion is false.

\(\ 20 \cdot n=4 \cdot 25\)	Cross multiply.
\(\ 20 n=100\)	You are looking for a number that when you multiply it by 20 you get 100.
\(\ \begin{array}{r} 5\ \\ 20\longdiv{100} \end{array}\)	You can find this value by dividing 100 by 20.