7.2.3: Circles

Last updated
Save as PDF

Page ID: 62474

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Identify properties of circles.
Find the circumference of a circle.
Find the area of a circle.
Find the area and perimeter of composite geometric figures.

Introduction

Circles are a common shape. You see them all over: wheels on a car, Frisbees passing through the air, compact discs delivering data. These are all circles.

A circle is a two-dimensional figure just like polygons and quadrilaterals. However, circles are measured differently than these other shapes. You even have to use some different terms to describe them. Let’s take a look at this interesting shape.

Properties of Circles

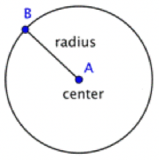
A circle represents a set of points, all of which are the same distance away from a fixed, middle point. This fixed point is called the center. The distance from the center of the circle (point A) to any point on the circle (point B) is called the radius. A circle is named by the point at its center, so this circle would be called Circle A.

$Screen Shot 2021-05-07 at 4.32.49 PM.png$

When two radii (the plural of radius) are put together to form a line segment across the circle, you have a diameter. The diameter of a circle passes through the center of the circle and has its endpoints on the circle itself.

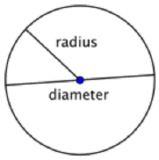
$Screen Shot 2021-05-07 at 4.37.44 PM.png$

The diameter of any circle is two times the length of that circle’s radius. It can be represented by the expression $\ 2r$, or “two times the radius.” So if you know a circle’s radius, you can multiply it by 2 to find the diameter; this also means that if you know a circle’s diameter, you can divide by 2 to find the radius.

Example

Find the diameter of the circle.

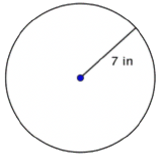
$Screen Shot 2021-05-07 at 4.41.38 PM.png$

Solution

$\ \begin{array}{c}
d=2 r \\
d=2(7) \\
d=14
\end{array}$

The diameter is two times the radius, or $\ 2r$. The radius of this circle is 7 inches, so the diameter is $\ 2(7)=14$ inches.

The diameter is 14 inches.

Example

Find the radius of the circle.

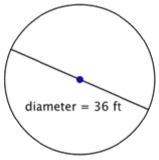
$Screen Shot 2021-05-07 at 4.46.15 PM.png$

Solution

$\ \begin{array}{c}
r=\frac{1}{2} d \\
r=\frac{1}{2}(36) \\
r=18
\end{array}$

The radius is half the diameter, or $\ \frac{1}{2} d$. The diameter of this circle is 36 feet, so the radius is $\ \frac{1}{2}(36)=18$ feet.

The radius is 18 feet.

Circumference

The distance around a circle is called the circumference. (Recall, the distance around a polygon is the perimeter.)

One interesting property about circles is that the ratio of a circle’s circumference and its diameter is the same for all circles. No matter the size of the circle, the ratio of the circumference and diameter will be the same.

Some actual measurements of different items are provided below. The measurements are accurate to the nearest millimeter or quarter inch (depending on the unit of measurement used). Look at the ratio of the circumference to the diameter for each one. Although the items are different, the ratio for each is approximately the same.

Item	Circumference ($\ C$) (rounded to nearest hundredth)	Diameter ($\ d$)	Ratio $\ \frac{C}{d}$
Cup	253 mm	79 mm	$\ \frac{253}{79}=3.2025 \ldots$
Quarter	84 mm	27 mm	$\ \frac{84}{27}=3.1111 \ldots$
Bowl	37.25 inches	11.75 inches	$\ \frac{37.25}{11.75}=3.1702 \ldots$

The circumference and the diameter are approximate measurements, since there is no precise way to measure these dimensions exactly. If you were able to measure them more precisely, however, you would find that the ratio $\ \frac{C}{d}$ would move towards 3.14 for each of the items given. The mathematical name for the ratio $\ \frac{C}{d}$ is pi, and is represented by the Greek letter $\ \pi$.

$\ \pi$ is a non-terminating, non-repeating decimal, so it is impossible to write it out completely. The first 10 digits of $\ \pi$ are 3.141592653; it is often rounded to 3.14 or estimated as the fraction $\ \frac{22}{7}$. Note that both 3.14 and $\ \frac{22}{7}$ are approximations of $\ \pi$, and are used in calculations where it is not important to be precise.

Since you know that the ratio of circumference to diameter (or $\ \pi$) is consistent for all circles, you can use this number to find the circumference of a circle if you know its diameter.

$\ \frac{C}{d}=\pi, \text { so } C=\pi d$

$\ \text { Also, since } d=2 r, \text { then } C=\pi d=\pi(2 r)=2 \pi r$.

Circumference of a Circle

To find the circumference ($\ C$) of a circle, use one of the following formulas:

If you know the diameter ($\ d$) of a circle: $\ C=\pi d$

If you know the radius ($\ r$) of a circle: $\ C=2 \pi r$

Example

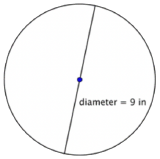
Find the circumference of the circle.

$Screen Shot 2021-05-08 at 3.01.28 PM.png$

Solution

$\ \begin{array}{l} C=\pi d \\ C=\pi \cdot 9 \\ C \approx 3.14 \cdot 9 \\ C \approx 28.26 \end{array}$	To calculate the circumference given a diameter of 9 inches, use the formula $\ C=\pi d$. Use 3.14 as an approximation for $\ \pi$.
	Since you are using an approximation for $\ \pi$, you cannot give an exact measurement of the circumference. Instead, you use the symbol $\ \approx$ to indicate “approximately equal to.”

The circumference is 9$\ \pi$ or approximately 28.26 inches.

Example

Find the circumference of a circle with a radius of 2.5 yards.

Solution

$\ \begin{array}{l}
C=2 \pi r \\
C=2 \pi \cdot 2.5 \\
C=\pi \cdot 5 \\
C \approx 3.14 \cdot 5 \\
C \approx 15.7
\end{array}$

To calculate the circumference of a circle given a radius of 2.5 yards, use the formula $\ C=2 \pi r$. Use 3.14 as an approximation for $\ \pi$.

The circumference is 5 $\ \pi$ or approximately 15.7 yards.

Exercise

A circle has a radius of 8 inches. What is its circumference, rounded to the nearest inch?

25 inches
50 inches
64 inches²
201 inches

Answer

Incorrect. You multiplied the radius times $\ \pi$; the correct formula for circumference when the radius is given is $\ C=2 \pi r$. The correct answer is 50 inches.
Correct. If the radius is 8 inches, the correct formula for circumference when the radius is given is $\ C=2 \pi r$. The correct answer is 50 inches.
Incorrect. It looks like you squared 8 and then multiplied 64 by $\ \pi$ to arrive at this answer. Remember that the formula for circumference when the radius is given is $\ C=2 \pi r$. The correct answer is 50 inches.

Area

$\ \pi$ is an important number in geometry. You have already used it to calculate the circumference of a circle. You use $\ \pi$ when you are figuring out the area of a circle, too.

Area of a Circle

To find the area ($\ A$) of a circle, use the formula: $\ A=\pi r^{2}$

Example

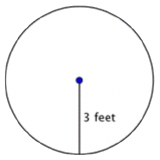
Find the area of the circle.

$Screen Shot 2021-05-08 at 3.21.57 PM.png$

Solution

$\ \begin{array}{l}
A=\pi r^{2} \\
A=\pi \cdot 3^{2} \\
A=\pi \cdot 9 \\
A \approx 3.14 \cdot 9 \\
A \approx 28.26
\end{array}$

To find the area of this circle, use the formula $\ A=\pi r^{2}$.

Remember to write the answer in terms of square units, since you are finding the area.

The area is 9$\ \pi$ or approximately 28.26 feet².

Exercise

A button has a diameter of 20 millimeters. What is the area of the button? Use 3.14 as an approximation of $\ \pi$.

62.8 mm
314 mm²
400 mm²
1256 mm²

Answer

Incorrect. You found the circumference of the button: $\ 20 \cdot 3.14=62.8$. To find the area, use the formula $\ A=\pi r^{2}$. The correct answer is 314 mm²

Composite Figures

Now that you know how to calculate the circumference and area of a circle, you can use this knowledge to find the perimeter and area of composite figures. The trick to figuring out these types of problems is to identify shapes (and parts of shapes) within the composite figure, calculate their individual dimensions, and then add them together.

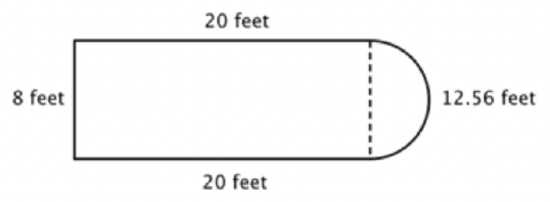
For example, look at the image below. Is it possible to find the perimeter?

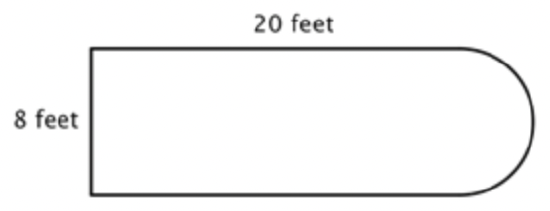
$Screen Shot 2021-05-08 at 3.35.08 PM.png$

The first step is to identify simpler figures within this composite figure. You can break it down into a rectangle and a semicircle, as shown below.

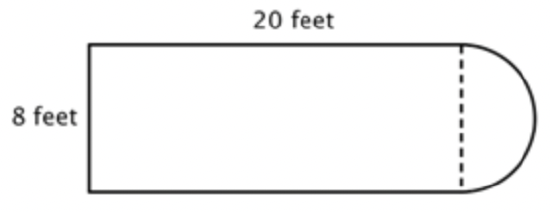
$Screen Shot 2021-05-08 at 3.36.05 PM.png$

You know how to find the perimeter of a rectangle, and you know how to find the circumference of a circle. Here, the perimeter of the three solid sides of the rectangle is $\ 8+20+20=48 \text { feet }$. (Note that only three sides of the rectangle will add into the perimeter of the composite figure because the other side is not at an edge; it is covered by the semicircle!)

To find the circumference of the semicircle, use the formula $\ C=\pi d$ with a diameter of 8 feet, then take half of the result. The circumference of the semicircle is 4$\ \pi$, or approximately 12.56 feet, so the total perimeter is about 60.56 feet.

$Screen Shot 2021-05-08 at 3.41.41 PM.png$

Example

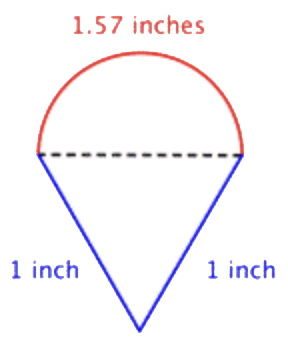
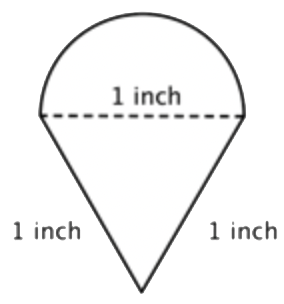
Find the perimeter (to the nearest hundredth) of the composite figure made up of a semi-circle and a triangle.

$Screen Shot 2021-05-08 at 3.47.43 PM.png$

Solution

$Screen Shot 2021-05-08 at 3.48.42 PM.png$

Identify smaller shapes within the composite figure. This figure contains a semicircle and a triangle.

$\ \begin{array}{l}
\text {Diameter }(d)=1\\ C=\pi d \\
C=\pi(1) \\
C=\pi
\end{array}$

Find the circumference of the circle. Then divide by 2 to find the circumference of the semi-circle.

Circumference of semicircle $\ =\frac{1}{2} \pi$ or approximately 1.57 inches

$\ 1+1+\frac{1}{2} \pi \approx 3.57 \text { inches }$

$Screen Shot 2021-05-08 at 4.11.51 PM.png$

Find the total perimeter by adding the circumference of the semicircle and the lengths of the two legs. Since our measurement of the semi-circle’s circumference is approximate, the perimeter will be an approximation also.

Approximately 3.57 inches

Example

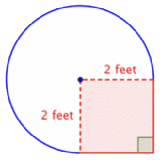
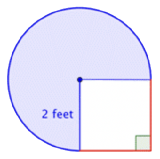
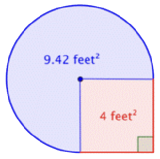
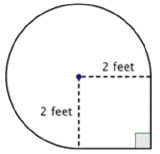
Find the area of the composite figure, made up of three-quarters of a circle and a square, to the nearest hundredth.

$Screen Shot 2021-05-08 at 4.13.23 PM.png$

Solution

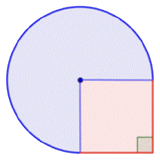$Screen Shot 2021-05-08 at 4.14.20 PM.png$	Identify smaller shapes within the composite figure. This figure contains a circular region and a square. If you find the area of each, you can find the area of the entire figure.
$Screen Shot 2021-05-08 at 4.15.52 PM.png$ $\ \begin{array}{l} \text { Area of square }&=s^{2} \\ \quad&=(2)^{2} \\ &=4 \mathrm{ft}^{2} \end{array}$	Find the area of the square.
$Screen Shot 2021-05-08 at 4.18.47 PM.png$ $\ \begin{array}{l} \text { Area of full circle }&=\pi r^{2} \\ \quad&=\pi(2)^{2} \\ &=4 \pi \mathrm{ft}^{2} \end{array}$	Find the area of the circular region. The radius is 2 feet.
$\ \begin{array}{c} \text{Area of region} = \frac{3}{4}\cdot4\pi\\ =3\pi\\ \approx3\cdot3.14\text{ ft}^2\\ \text{This is approximately } 9.42 \text{ feet}^2 \end{array}$	Note that the region is $\ \frac{3}{4}$ of a whole circle, so you need to multiply the area of the circle by $\ \frac{3}{4}$. Use 3.14 as an approximation for $\ \pi$.
$Screen Shot 2021-05-08 at 4.32.33 PM.png$ $\ 4 \text { feet}^{2}+3 \pi \text { feet}^{2}=\text { approximately } 13.42 \text { feet}^{2}$	Add the two regions together. Since your measurement of the circular’s area is approximate, the area of the figure will be an approximation also.

The area is approximately $\ 13.42 \text { feet }^{2}$.

Exercise

What is the area (to the nearest hundredth) of the figure shown below? (Both rounded regions are semi-circles.)

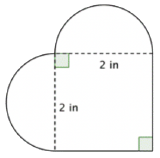
$Screen Shot 2021-05-08 at 4.36.26 PM.png$

16.56 in²
7.14 in²
4 in²
3.14 in²

Answer

Summary

Circles are an important geometric shape. The distance around a circle is called the circumference, and the interior space of a circle is called the area. Calculating the circumference and area of a circle requires a number called pi ($\ \pi$), which is a non-terminating, non-repeating decimal. Pi is often approximated by the values 3.14 and $\ \frac{22}{7}$. You can find the perimeter or area of composite shapes, including shapes that contain circular sections, by applying the circumference and area formulas where appropriate.

Item	Circumference (\(\ C\)) (rounded to nearest hundredth)	Diameter (\(\ d\))	Ratio \(\ \frac{C}{d}\)
Cup	253 mm	79 mm	\(\ \frac{253}{79}=3.2025 \ldots\)
Quarter	84 mm	27 mm	\(\ \frac{84}{27}=3.1111 \ldots\)
Bowl	37.25 inches	11.75 inches	\(\ \frac{37.25}{11.75}=3.1702 \ldots\)

\(\ \begin{array}{l} C=\pi d \\ C=\pi \cdot 9 \\ C \approx 3.14 \cdot 9 \\ C \approx 28.26 \end{array}\)	To calculate the circumference given a diameter of 9 inches, use the formula \(\ C=\pi d\). Use 3.14 as an approximation for \(\ \pi\).
	Since you are using an approximation for \(\ \pi\), you cannot give an exact measurement of the circumference. Instead, you use the symbol \(\ \approx\) to indicate “approximately equal to.”