14.2.2: The Elimination Method

Learning Objectives

• Solve a system of equations when no multiplication is necessary to eliminate a variable.
• Solve a system of equations when multiplication is necessary to eliminate a variable.
• Recognize systems that have no solution or an infinite number of solutions.
• Solve application problems using the elimination method.

Introduction

The elimination method for solving systems of linear equations uses the addition property of equality. You can add the same value to each side of an equation.

So if you have a system: \(\ x-y=-6\) and \(\ x+y=8\), you can add \(\ x+y\) to the left side of the first equation and add 8 to the right side of the equation. And since \(\ x+y=8\), you are adding the same value to each side of the first equation.

Using Addition to Eliminate a Variable

If you add the two equations, \(\ x-y=-6\) and \(\ x+y=8\) together, as noted above, watch what happens.

\(\ \begin{array}{rr}
x-y= & -6 \\
x+y= & 8 \\
\hline 2 x+0= & 2
\end{array}\)

You have eliminated the \(\ y\) term, and this equation can be solved using the methods for solving equations with one variable.

Let’s see how this system is solved using the elimination method.

Example

Use elimination to solve the system.

\(\ \begin{array}{c}
x-y=-6 \\
x+y=8
\end{array}\)

Solution

\(\ \begin{array}{r} x-y= & -6 \\ +\quad x+y= & 8 \\ \hline 2 x \ \ \ \ \ \ \ =&2 \end{array}\)	Add the equations.
\(\ \begin{aligned} 2 x &=2 \\ x &=1 \end{aligned}\)	Solve for \(\ x\).
\(\ \begin{array}{r} x+y=8 \\ 1+y=8 \\ y=8-1 \\ y=7 \end{array}\)	Substitute \(\ x=1\) into one of the original equations and solve for \(\ y\).
\(\ \begin{array}{r} x-y=-6 \\ 1-7=-6 \\ -6=-6 \end{array}\) \(\ \begin{aligned} x+y &=8 \\ 1+7 &=8 \\ 8 &=8 \end{aligned}\) TRUE TRUE	Be sure to check your answer in both equations! The answers check.

The solution is \(\ (1,7)\).

Unfortunately, not all systems work out this easily. How about a system like \(\ 2 x+y=12\) and \(\ -3 x+y=2\)? If you add these two equations together, no variables are eliminated.

\(\ \begin{aligned}
2 x+y&=12 \\
-3 x+y&=2 \\
\hline-x+2 y&=14
\end{aligned}\)

But you want to eliminate a variable. So let’s add the opposite of one of the equations to the other equation.

\(\ \begin{array}{r}
2 x+y=12 \quad \rightarrow& 2 x+y=12\quad \rightarrow& \quad 2 x+y=\ 12 \\
-3 x+y=2 \quad\rightarrow&-(-3 x+y)=-(2)\quad \rightarrow& \quad \underline{3x-y=-2}\\
&& 5x+0y=\ 10
\end{array}\)

You have eliminated the \(\ y\) variable, and the problem can now be solved. See the example below.

Example

Use elimination to solve the system.

\(\ \begin{aligned}
2 x+y&=12 \\
-3 x+y&=2
\end{aligned}\)

Solution

\(\ \begin{aligned} 2 x+y&=12 \\ -3 x+y&=2 \end{aligned}\)	You can eliminate the y-variable if you add the opposite of one of the equations to the other equation.
\(\ \begin{aligned} 2 x+y&=12 \\ 3 x-y&=-2 \\ 5 x&=10 \end{aligned}\)	Rewrite the second equation as its opposite. Add.
\(\ x=2\)	Solve for \(\ x\).
\(\ \begin{array}{r} 2(2)+y=12 \\ 4+y=12 \\ y=8 \end{array}\)	Substitute \(\ x=2\) into one of the original equations and solve for \(\ y\).
\(\ \begin{array}{r} 2 x+y=12 \\ 2(2)+8=12 \\ 4+8=12 \\ 12=12 \end{array}\) \(\ \begin{array}{r} -3 x+y=2 \\ -3(2)+8=2 \\ -6+8=2 \\ 2=2 \end{array}\) TRUE TRUE	Be sure to check your answer in both equations! The answers check.

The solution is \(\ (2,8)\).

The following are two more examples showing how to solve linear systems of equations using elimination.

Example

Use elimination to solve the system.

\(\ \begin{aligned}
-2 x+3 y&=-1 \\
2 x+5 y&=25
\end{aligned}\)

Solution

\(\ \begin{aligned} -2 x+3 y &=-1 \\ 2 x+5 y &=25 \end{aligned}\)	Notice the coefficients of each variable in each equation. If you add these two equations, the \(\ x\) term will be eliminated since \(\ -2 x+2 x=0\).
\(\ \begin{array}{rr} -2 x+3 y= & -1 \\ 2 x+5 y= & 25 \\ \hline 8 y= & 24 \\ y= & 3 \end{array}\)	Add and solve for \(\ y\).
\(\ \begin{aligned} 2 x+5 y&=25 \\ 2 x+5(3)&=25 \\ 2 x+15&=25 \\ 2 x&=10 \\ x&=5 \end{aligned}\)	Substitute \(\ y=3\) into one of the original equations.
\(\ \begin{aligned} -2 x+3 y &=-1 \\ -2(5)+3(3) &=-1 \\ -10+9 &=-1 \\ -1 &=-1 \end{aligned}\) \(\ \begin{array}{r} 2 x+5 y=25 \\ 2(5)+5(3)=25 \\ 10+15=25 \\ 25=25 \end{array}\) TRUE TRUE	Check solutions. The answers check.

The solution is \(\ (5,3)(5,3)\).

Example

Use elimination to solve for \(\ x\) and \(\ y\).

Solution

\(\ \begin{array}{l} 4 x+2 y=14 \\ 5 x+2 y=16 \end{array}\)	Notice the coefficients of each variable in each equation. You will need to add the opposite of one of the equations to eliminate the variable \(\ y\), as \(\ 2 y+2 y=4 y\), but \(\ 2 y+(-2 y)=0\).
\(\ \begin{array}{r} 4 x+2 y= & 14 \\ -5 x-2 y= & -16 \\ \hline-x \ \ \ \ \ \ \ \ \ = & -2 \\ x\ \ \ \ \ \ \ \ \ = & 2 \end{array}\)	Change one of the equations to its opposite, add and solve for \(\ x\).
\(\ \begin{aligned} 4 x+2 y=&14 \\ 4(2)+2 y=&14 \\ 8+2 y=&14 \\ 2 y=&6 \\ y=&3 \end{aligned}\)	Substitute \(\ x=2\) into one of the original equations and solve for \(\ y\).

The solution is \(\ (2,3)\).

Go ahead and check this last example—substitute \(\ (2,3)\) into both equations. You get two true statements: \(\ 14=14\) and \(\ 16=16\)!

Notice that you could have used the opposite of the first equation rather than the second equation and gotten the same result.

Using Multiplication and Addition to Eliminate a Variables

Many times, adding the equations or adding the opposite of one of the equations will not result in eliminating a variable. Look at the system below.

\(\ \begin{aligned}
3 x+4 y=52 \\
5 x+y=30
\end{aligned}\)

If you add the equations above, or add the opposite of one of the equations, you will get an equation that still has two variables. So let’s now use the multiplication property of equality first. You can multiply both sides of one of the equations by a number that will result in the coefficient of one of the variables being the opposite of the same variable in the other equation.

This is where multiplication comes in handy. The first equation contains the term \(\ 4y\) and the second equation contains the term \(\ y\). If you multiply the second equation by -4, when you add both equations, the \(\ y\) variables will add up to 0.

\(\ \begin{array}{l}
3 x+4 y=52 \quad&\rightarrow \quad3 x+4 y=52 \quad&\rightarrow \quad3 x+4 y= 52 \\
5 x+y=30 \quad&\rightarrow \quad-4(5 x+y)=-4(30) \quad&\rightarrow \quad\underline{-20 x-4 y=-120}\\
&&\quad-17x+0y=-68
\end{array}\)

See the example below.

Example

Solve for \(\ x\) and \(\ y\).

Equation A: \(\ 3 x+4 y=52\)

Equation B: \(\ 5 x+y=30\)

Solution

\(\ \begin{array}{r} 3 x+4 y=52 \\ 5 x+\ \ y=30 \end{array}\)	Look for terms that can be eliminated. The equations do not have any \(\ x\) or \(\ y\) terms with the same coefficients.
\(\ \begin{aligned} 3 x+4 y&=52 \\ -4 (5 x+y)&=-4(30) \\ \hline \end{aligned}\)	Multiply the second equation by -4 so they have the same coefficient.
\(\ \begin{array}{rr} 3 x+4 y= & 52 \\ -20 x-4 y= & -120 \\ \hline \end{array}\)	Rewrite the system, and add the equations.
\(\ \begin{aligned} -17 x &=-68 \\ x &=4 \end{aligned}\)	Solve for \(\ x\).
\(\ \begin{array}{r} 3 x+4 y=52 \\ 3(4)+4 y=52 \\ 12+4 y=52 \\ 4 y=40 \\ y=10 \end{array}\)	Substitute \(\ x=4\) into one of the original equations to find \(\ y\).
\(\ \begin{array}{r} 3 x+4 y=52 \\ 3(4)+4(10)=52 \\ 12+40=52 \\ 52=52 \end{array}\) \(\ \begin{array}{r} 5 x+y=30 \\ 5(4)+10=30 \\ 20+10=30 \\ 30=30 \end{array}\) TRUE TRUE	Check your answer. The answers check.

The solution is \(\ (4,10)\).

There are other ways to solve this system. Instead of multiplying one equation in order to eliminate a variable when the equations were added, you could have multiplied both equations by different numbers.

Let’s remove the variable \(\ x\) this time. Multiply Equation A by 5 and Equation B by -3.

Example

Solve for \(\ x\) and \(\ y\).

\(\ \begin{array}{r}
3 x+4 y=52 \\
5 x+\ \ y=30
\end{array}\)

Solution

\(\ \begin{array}{r} 3 x+4 y=52 \\ 5 x+\ \ y=30 \end{array}\)	Look for terms that can be eliminated. The equations do not have any \(\ x\) and \(\ y\) terms with the same coefficient.
\(\ \begin{aligned} 5(3 x+4 y) &=5(52) \\ 5 x+\ y\ \ &=0 \end{aligned}\) \(\ \begin{aligned} 15 x+20 y&=260\\ 5 x+y&=30 \end{aligned}\)	In order to use the elimination method, you have to create variables that have the same coefficient—then you can eliminate them. Multiply the top equation by 5.
\(\ \begin{aligned} 15 x+20 y&=260 \\ -3(5 x+\ \ y)&=-3(30) \end{aligned}\) \(\ \begin{array}{r} 15 x+20 y=& 260 \\ -15 x-\ \ 3 y=&-90 \end{array}\)	Now multiply the bottom equation by -3.
\(\ \begin{array}{r} 15 x+20 y &=&+260 \\ -15 x-\ \ 3 y &=&- 90 \\ \hline 17 y &=& 170 \\ y &=& 10 \end{array}\)	Next add the equations, and solve for \(\ y\).
\(\ \begin{aligned} 3 x+4 y&=52 \\ 3 x+4(10)&=52 \\ 3 x+40&=52 \\ 3 x&=12 \\ x&=4 \end{aligned}\)	Substitute \(\ y=10\) into one of the original equations to find \(\ x\).
The solution is \(\ (4,10)\).	You arrive at the same solution as before.

These equations were multiplied by 5 and -3 respectively, because that gave you terms that would add up to 0. Be sure to multiply all of the terms of the equation.

Exercise

Felix needs to find \(\ x\) and \(\ y\) in the following system.

Equation A: \(\ 7 y-4 x=5\)

Equation B: \(\ 3 y+4 x=25\)

If he wants to use the elimination method to eliminate one of the variables, which is the most efficient way for him to do so?

1. Add Equation A and Equation B
2. Add \(\ 4x\) to both sides of Equation A
3. Multiply Equation A by 5
4. Multiply Equation B by -1

Answer

1. Correct. If Felix adds the two equations, the terms \(\ 4x\) and \(\ -4 x\) will cancel out, leaving \(\ 10 y=30\). Felix will then easily be able to solve for \(\ y\).
2. Incorrect. Adding \(\ 4 x\) to both sides of Equation A will not change the value of the equation, nor will it help eliminate either of the variables—Felix will end up with the rewritten equation \(\ 7 y=5+4 x\). The correct answer is to add Equation A and Equation B.
3. Incorrect. Multiplying Equation A by 5 yields \(\ 35 y-20 x=25\), which does not help Felix eliminate any of the variables in the system. Felix may notice that now both equations have a constant of 25, but subtracting one from another is not an efficient way of solving this problem. Instead, it would create another equation where both variables are present. The correct answer is to add Equation A and Equation B.
4. Incorrect. Multiplying Equation B by -1 yields \(\ -3 y-4 x=-25\), which does not help Felix eliminate any of the variables in the system. Felix may notice that now both equations have a term of \(\ -4 x\), but adding them would not eliminate them, it would give him a \(\ -8 x\). The correct answer is to add Equation A and Equation B.

Special Situations

Just as with the substitution method, the elimination method will sometimes eliminate both variables, and you end up with either a true statement or a false statement. Recall that a false statement means that there is no solution.

Let’s look at an example.

Example

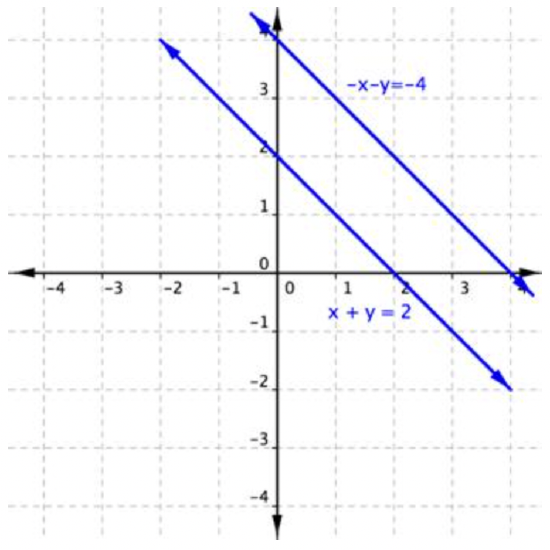
Solve for \(\ x\) and \(\ y\).

\(\ \begin{array}{c}
-x-y=-4 \\
x+y=2
\end{array}\)

Solution

\(\ \begin{array}{r} -x-y&=&-4 \\ x+y&=&2 \\ \hline 0&=&-2 \end{array}\)

Add the equations to eliminate the x-term.

There is no solution.

Graphing these lines shows that they are parallel lines and as such do not share any point in common, verifying that there is no solution.

If both variables are eliminated and you are left with a true statement, this indicates that there are an infinite number of ordered pairs that satisfy both of the equations. In fact, the equations are the same line.

Example

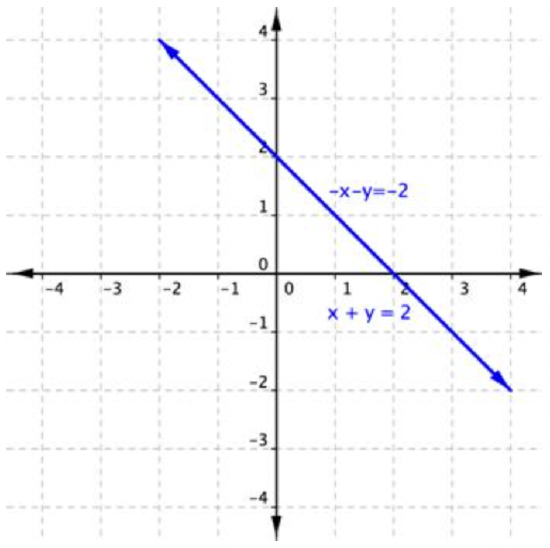
Solve for \(\ x\) and \(\ y\).

\(\ \begin{array}{r}
x+y&=&2 \\
-x-y&=&-2
\end{array}\)

Solution

\(\ \begin{array}{r} x+y&=&2 \\ -x-y&=&-2 \\ \hline 0&=&0 \end{array}\)

Add the equations to eliminate the x-term.

There are an infinite number of solutions.

Graphing these two equations will help to illustrate what is happening.

Solving Application Problems Using the Elimination Method

The elimination method can be applied to solving systems of equations that model real situations. Two examples of using the elimination method in problem solving are shown below.

Example

The sum of two numbers is 10. Their difference is 6. What are the two numbers?

Solution

\(\ \begin{array}{r} x+y&=&10 \\ x-y&=&6 \end{array}\)	Write a system of equations to model the situation. \(\ x\)=one number \(\ y\)=the other number
\(\ \begin{array}{r} x+y &=&10 \\ +\quad x-y &=&6 \\ \hline 2 x &=&16 \\ x &=&8 \end{array}\)	Add the equations to eliminate the y-term and then solve for \(\ x\).
\(\ \begin{array}{r} x+y&=&10 \\ 8+y&=&10 \\ y&=&2 \end{array}\)	Substitute the value for \(\ x\) into one of the original equations to find \(\ y\).
\(\ \begin{array}{r} x+y=10 \\ 8+2=10 \\ 10=10 \end{array}\) \(\ \begin{array}{r} x-y=6 \\ 8-2=6 \\ 6=6 \end{array}\) TRUE TRUE	Check your answer by substituting \(\ x=8\) and \(\ y=2\) into the original system. The answers check.

The numbers are 8 and 2.

Example

A theater sold 800 tickets for Friday night’s performance. One child ticket costs $4.50 and one adult ticket costs $6.00. The total amount collected was $4,500. How many of each type of ticket were sold?

Solution

The total number of tickets sold is \(\ 800\). \(\ a+c=800\) The amount of money collected is \(\ $4,500\) \(\ 6 a+4.5 c=4,500\) System of equations: \(\ a+c=800\) \(\ 6 a+4.5 c=4,500\)	Write a system of equations to model the ticket sale situation. \(\ a\)=number of adult tickets sold \(\ c\)=number of child tickets sold
\(\ \begin{array}{r} 6(a+c)=6(800) \\ 6 a+4.5 c=4,500 \end{array}\) \(\ \begin{array}{r} 6 a+6 c=4,800 \\ 6 a+4.5 c=4,500 \end{array}\)	Use multiplication to re-write the first equation.
\(\ \begin{array}{r} 6 a+6 c&=&4,800 \\ -6 a-4.5 c&=&-4,500 \\ \hline 1.5 c&=&300 \end{array}\) \(\ c= 200\)	Add the opposite of the second equation to eliminate a term and solve for \(\ c\).
\(\ \begin{array}{r} a+200&=&800 \\ -200&&-200 \\ \hline a&=&600 \end{array}\)	Substitute 200 in for \(\ c\) in one of the original equations.
\(\ \begin{aligned} a+c &=800 \\ 600+200 &=800 \\ 800 &=800 \end{aligned}\) \(\ \begin{array}{r} 6 a+4.5 c=4,500 \\ 6(600)+4.5(200)=4,500 \\ 3,600+900=4,500 \\ 4500=4,500 \end{array}\) TRUE TRUE	Check your answer by substituting \(\ a=600\) and \(\ c=200\) into the original system. The answers check.

600 adult tickets and 200 child tickets were sold.

Summary

Combining equations is a powerful tool for solving a system of equations. Adding or subtracting two equations in order to eliminate a common variable is called the elimination (or addition) method. Once one variable is eliminated, it becomes much easier to solve for the other one. Multiplication can be used to set up matching terms in equations before they are combined. When using multiplication in the elimination method, it is important to multiply all the terms on both sides of the equation—not just the one term you are trying to eliminate.