2.16: Exercises

Last updated
Save as PDF

Page ID: 36259

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

To decide on a new website design, the designer asks people to rank three designs that have been created (labeled A, B, and C). The individual ballots are shown below. Create a preference table.

ABC, ABC, ACB, BAC, BCA, BCA, ACB, CAB, CAB, BCA, ACB, ABC

To decide on a movie to watch, a group of friends all vote for one of the choices (labeled A, B, and C). The individual ballots are shown below. Create a preference table.

CAB, CBA, BAC, BCA, CBA, ABC, ABC, CBA, BCA, CAB, CAB, BAC

The planning committee for a renewable energy trade show is trying to decide what city to hold their next show in. The votes are shown below.

$\begin{array}{|c|c|c|c|c|}
\hline \textbf { Number of voters } & \textbf { 9 } & \textbf { 19 } & \textbf { 11 } & \textbf { 8 } \\
\hline \textbf { 1st choice } & \text { Buffalo } & \text { Atlanta } & \text { Chicago } & \text { Buffalo } \\
\hline \textbf { 2nd choice } & \text { Atlanta } & \text { Buffalo } & \text { Buffalo } & \text { Chicago } \\
\hline \textbf { 3rd choice } & \text { Chicago } & \text { Chicago } & \text { Atlanta } & \text { Atlanta } \\
\hline
\end{array}$

How many voters voted in this election?
How many votes are needed for a majority? A plurality?
Find the winner under the plurality method.
Find the winner under the Borda Count Method.
Find the winner under the Instant Runoff Voting method.
Find the winner under Copeland’s method.

A non-profit agency is electing a new chair of the board. The votes are shown below.

$\begin{array}{|c|c|c|c|c|}
\hline \textbf { Number of voters } & \mathbf{1 1} & \mathbf{5} & \mathbf{1 0} & \mathbf{3} \\
\hline \textbf { 1st choice } & \text { Atkins } & \text { Cortez } & \text { Burke } & \text { Atkins } \\
\hline \textbf { 2nd choice } & \text { Cortez } & \text { Burke } & \text { Cortez } & \text { Burke } \\
\hline \textbf { 3rd choice } & \text { Burke } & \text { Atkins } & \text { Atkins } & \text { Cortez } \\
\hline
\end{array}$

How many voters voted in this election?
How many votes are needed for a majority? A plurality?
Find the winner under the plurality method.
Find the winner under the Borda Count Method.
Find the winner under the Instant Runoff Voting method.
Find the winner under Copeland’s method.

The student government is holding elections for president. There are four candidates (labeled A, B, C, and D for convenience). The preference schedule for the election is:

$\begin{array}{|c|c|c|c|c|c|c|}
\hline \textbf {Number of voters} & \mathbf{1 2 0} & \mathbf{5 0} & \mathbf{4 0} & \mathbf{9 0} & \mathbf{6 0} & \mathbf{1 0 0} \\
\hline \textbf {1st choice } & \mathrm{C} & \mathrm{B} & \mathrm{D} & \mathrm{A} & \mathrm{A} & \mathrm{D} \\
\hline \textbf{2nd choice } & \mathrm{D} & \mathrm{C} & \mathrm{A} & \mathrm{C} & \mathrm{D} & \mathrm{B} \\
\hline \textbf{3rd choice } & \mathrm{B} & \mathrm{A} & \mathrm{B} & \mathrm{B} & \mathrm{C} & \mathrm{A} \\
\hline \textbf{4th choice } & \mathrm{A} & \mathrm{D} & \mathrm{C} & \mathrm{D} & \mathrm{B} & \mathrm{C} \\
\hline
\end{array}$

How many voters voted in this election?
How many votes are needed for a majority? A plurality?
Find the winner under the plurality method.
Find the winner under the Borda Count Method.
Find the winner under the Instant Runoff Voting method.
Find the winner under Copeland’s method.

The homeowners association is deciding a new set of neighborhood standards for architecture, yard maintenance, etc. Four options have been proposed. The votes are:

$\begin{array}{|c|c|c|c|c|c|c|}
\hline \textbf { Number of voters } & \mathbf{8} & \mathbf{9} & \mathbf{1 1} & \mathbf{7} & \mathbf{7} & \mathbf{5} \\
\hline \textbf { 1st choice } & \text { B } & \text { A } & \text { D } & \text { A } & \text { B } & \text { C } \\
\hline \textbf { 2nd choice } & \text { C } & \text { D } & \text { B } & \text { B } & \text { A } & \text { D } \\
\hline \textbf { 3rd choice } & \text { A } & \text { C } & \text { C } & \text { D } & \text { C } & \text { A } \\
\hline \textbf { 4th choice } & \text { D } & \text { B } & \text { A } & \text { C } & \text { D } & \text { B } \\
\hline
\end{array}$

How many voters voted in this election?
How many votes are needed for a majority? A plurality?
Find the winner under the plurality method.
Find the winner under the Borda Count Method.
Find the winner under the Instant Runoff Voting method.
Find the winner under Copeland’s method.

Consider an election with 129 votes.
1. If there are 4 candidates, what is the smallest number of votes that a plurality candidate could have?
2. If there are 8 candidates, what is the smallest number of votes that a plurality candidate could have?

Consider an election with 953 votes.
1. If there are 7 candidates, what is the smallest number of votes that a plurality candidate could have?
2. If there are 8 candidates, what is the smallest number of votes that a plurality candidate could have?

Does this voting system having a Condorcet Candidate? If so, find it.

$\begin{array}{|c|c|c|c|}
\hline \textbf { Number of voters } & \mathbf{1 4} & \mathbf{1 5} & \mathbf{2} \\
\hline \textbf { 1st choice } & \mathrm{A} & \mathrm{C} & \mathrm{B} \\
\hline \textbf { 2nd choice } & \mathrm{B} & \mathrm{B} & \mathrm{C} \\
\hline \textbf { 3rd choice } & \mathrm{C} & \mathrm{A} & \mathrm{A} \\
\hline
\end{array}$

Does this voting system having a Condorcet Candidate? If so, find it.

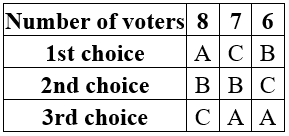
$clipboard_eecd05381cdae5dd73621622d8604dc6b.png$

The marketing committee at a company decides to vote on a new company logo. They decide to use approval voting. Their results are tallied below. Each column shows the number of voters with the particular approval vote. Which logo wins under approval voting?

$\begin{array}{|c|c|c|c|}
\hline \textbf { Number of voters } & \mathbf{8} & \mathbf{7} & \mathbf{6} \\
\hline \textbf { 1st choice } & \mathrm{A} & \mathrm{C} & \mathrm{B} \\
\hline \textbf { 2nd choice } & \mathrm{B} & \mathrm{B} & \mathrm{C} \\
\hline \textbf { 3rd choice } & \mathrm{C} & \mathrm{A} & \mathrm{A} \\
\hline
\end{array}$

The downtown business association is electing a new chairperson, and decides to use approval voting. The tally is below, where each column shows the number of voters with the particular approval vote. Which candidate wins under approval voting?

$\begin{array}{|c|c|c|c|c|c|c|c|}
\hline \textbf { Number of voters } & \mathbf{8} & \mathbf{7} & \mathbf{6} & \mathbf{3} & \mathbf{4} & \mathbf{2} & \mathbf{5} \\
\hline \mathbf{A} & \mathrm{X} & \mathrm{X} & & & \mathrm{X} & & \mathrm{X} \\
\hline \mathbf{B} & \mathrm{X} & & \mathrm{X} & \mathrm{X} & & & \mathrm{X} \\
\hline \mathbf{C} & & \mathrm{X} & \mathrm{X} & \mathrm{X} & & \mathrm{X} & \\
\hline \mathbf{D} & \mathrm{X} & & \mathrm{X} & & \mathrm{X} & \mathrm{X} & \\
\hline
\end{array}$

Search

Text Color

Text Size

Margin Size

Font Type