8.7: Exercises

Last updated
Save as PDF

Page ID: 34224

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Skills

Marko currently has 20 tulips in his yard. Each year he plants 5 more.
1. Write a recursive formula for the number of tulips Marko has
2. Write an explicit formula for the number of tulips Marko has

Pam is a Disc Jockey. Every week she buys 3 new albums to keep her collection current. She currently owns 450 albums.
1. Write a recursive formula for the number of albums Pam has
2. Write an explicit formula for the number of albums Pam has

A store’s sales (in thousands of dollars) grow according to the recursive rule $P_n=P_{n-1} + 15$, with initial population $P_0=40$.
1. Calculate $P_1$ and $P_2$
2. Find an explicit formula for $P_n$
3. Use your formula to predict the store’s sales in 10 years
4. When will the store’s sales exceed $100,000?

The number of houses in a town has been growing according to the recursive rule $P_n=P_{n-1} + 30$, with initial population $P_0=200$.
1. Calculate $P_1$ and $P_2$
2. Find an explicit formula for $P_n$
3. Use your formula to predict the number of houses in 10 years
4. When will the number of houses reach 400 houses?

A population of beetles is growing according to a linear growth model. The initial population (week 0) was $P_0=3$, and the population after 8 weeks is $P_8=67$.
1. Find an explicit formula for the beetle population in week $n$
2. After how many weeks will the beetle population reach 187?

The number of streetlights in a town is growing linearly. Four months ago $(n = 0)$ there were 130 lights. Now $(n = 4)$ there are 146 lights. If this trend continues,
1. Find an explicit formula for the number of lights in month $n$
2. How many months will it take to reach 200 lights?

Tacoma's population in 2000 was about 200 thousand, and had been growing by about 9% each year.
1. Write a recursive formula for the population of Tacoma
2. Write an explicit formula for the population of Tacoma
3. If this trend continues, what will Tacoma's population be in 2016?
4. When does this model predict Tacoma’s population to exceed 400 thousand?

Portland's population in 2007 was about 568 thousand, and had been growing by about 1.1% each year.
1. Write a recursive formula for the population of Portland
2. Write an explicit formula for the population of Portland
3. If this trend continues, what will Portland's population be in 2016?
4. If this trend continues, when will Portland’s population reach 700 thousand?

Diseases tend to spread according to the exponential growth model. In the early days of AIDS, the growth rate was around 190%. In 1983, about 1700 people in the U.S. died of AIDS. If the trend had continued unchecked, how many people would have died from AIDS in 2005?

The population of the world in 1987 was 5 billion and the annual growth rate was estimated at 2 percent per year. Assuming that the world population follows an exponential growth model, find the projected world population in 2015.

A bacteria culture is started with 300 bacteria. After 4 hours, the population has grown to 500 bacteria. If the population grows exponentially,
1. Write a recursive formula for the number of bacteria
2. Write an explicit formula for the number of bacteria
3. If this trend continues, how many bacteria will there be in 1 day?
4. How long does it take for the culture to triple in size?

A native wolf species has been reintroduced into a national forest. Originally 200 wolves were transplanted. After 3 years, the population had grown to 270 wolves. If the population grows exponentially,
1. Write a recursive formula for the number of wolves
2. Write an explicit formula for the number of wolves
3. If this trend continues, how many wolves will there be in 10 years?
4. If this trend continues, how long will it take the population to grow to 1000 wolves?

One hundred trout are seeded into a lake. Absent constraint, their population will grow by 70% a year. The lake can sustain a maximum of 2000 trout. Using the logistic growth model,
1. Write a recursive formula for the number of trout
2. Calculate the number of trout after 1 year and after 2 years.

Ten blackberry plants started growing in my yard. Absent constraint, blackberries will spread by 200% a month. My yard can only sustain about 50 plants. Using the logistic growth model,
1. Write a recursive formula for the number of blackberry plants in my yard
2. Calculate the number of plants after 1, 2, and 3 months

In 1968, the U.S. minimum wage was $1.60 per hour. In 1976, the minimum wage was $2.30 per hour. Assume the minimum wage grows according to an exponential model where n represents the time in years after 1960.
1. Find an explicit formula for the minimum wage.
2. What does the model predict for the minimum wage in 1960?
3. If the minimum wage was $5.15 in 1996, is this above, below or equal to what the model predicts?

Concepts

The population of a small town can be described by the equation $P_n = 4000 + 70n$, where $n$ is the number of years after 2005. Explain in words what this equation tells us about how the population is changing.

The population of a small town can be described by the equation $P_n = 4000(1.04)n$, where $n$ is the number of years after 2005. Explain in words what this equation tells us about how the population is changing.

Exploration

Most of the examples in the text examined growing quantities, but linear and exponential equations can also describe decreasing quantities, as the next few problems will explore.

A new truck costs $32,000. The car’s value will depreciate over time, which means it will lose value. For tax purposes, depreciation is usually calculated linearly. If the truck is worth $24,500 after three years, write an explicit formula for the value of the car after $n$ years.

Inflation causes things to cost more, and for our money to buy less (hence your grandparents saying, "In my day, you could buy a cup of coffee for a nickel"). Suppose inflation decreases the value of money by 5% each year. In other words, if you have $1 this year, next year it will only buy you $0.95 worth of stuff. How much will $100 buy you in 20 years?

Suppose that you have a bowl of 500 M&M candies, and each day you eat $\frac{1}{4}$ of the candies you have. Is the number of candies left changing linearly or exponentially? Write an equation to model the number of candies left after n days.

A warm object in a cooler room will decrease in temperature exponentially, approaching the room temperature according to the formula where Tn is the temperature after n minutes, $r$ is the rate at which temperature is changing, a is a constant, and Tr is the temperature of the room. Forensic investigators can use this to predict the time of death of a homicide victim. Suppose that when a body was discovered $(n = 0)$ it was 85 degrees. After 20 minutes, the temperature was measured again to be 80 degrees. The body was in a 70 degree room.
1. Use the given information with the formula provided to find a formula for the temperature of the body.
2. When did the victim die, if the body started at 98.6 degrees?

Recursive equations can be very handy for modeling complicated situations for which explicit equations would be hard to interpret. As an example, consider a lake in which 2000 fish currently reside. The fish population grows by 10% each year, but every year 100 fish are harvested from the lake by people fishing.
1. Write a recursive equation for the number of fish in the lake after n years.
2. Calculate the population after 1 and 2 years. Does the population appear to be increasing or decreasing?
3. What is the maximum number of fish that could be harvested each year without causing the fish population to decrease in the long run?

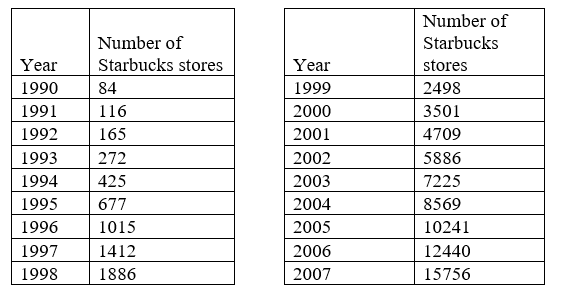
The number of Starbucks stores grew after first opened. The number of stores from 1990-2007, as reported on their corporate website[1], is shown below.
1. Carefully plot the data. Does is appear to be changing linearly or exponentially?
2. Try finding an equation to model the data by picking two points to work from. How well does the equation model the data?
3. Try using an equation of the form , where k is a constant, to model the data. This type of model is called a Power model. Compare your results to the results from part $b$. Note: to use this model, you will need to have 1990 correspond with $n = 1$ rather than $n = 0$.

$clipboard_e723972894bc819360fb5aa9fe3e212fd.png$

Thomas Malthus was an economist who put forth the principle that population grows based on an exponential growth model, while food and resources grow based on a linear growth model. Based on this, Malthus predicted that eventually demand for food and resources would out outgrow supply, with doom-and-gloom consequences. Do some research about Malthus to answer these questions.
1. What societal changes did Malthus propose to avoid the doom-and-gloom outcome he was predicting?
2. Why do you think his predictions did not occur?
3. What are the similarities and differences between Malthus's theory and the logistic growth model?

[1] www.starbucks.com/aboutus/Company_Timeline.pdf retrieved May 2009

Search

Text Color

Text Size

Margin Size

Font Type