4.11: Problem Bank
- Page ID
- 10588
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Harriet is part of a group of five children who share four pies. Jeff is part of a group of seven children who share four pies. Jean is part of a group of seven children who share six pies.
- Who gets more pie, Harriet or Jeff? Justify your answer!
- Who gets more pie, Jeff or Jean? Justify your answer!
- Who gets more pie, Harriet or Jean? Justify your answer!
Yesterday was Zoe’s birthday, and she had a big rectangular cake. Today, \(\frac{2}{5}\) of the cake is left. The leftover cake is shown here.

Draw a picture of the original (whole) cake and explain your work.
Use benchmarks and intuitive methods to arrange the fractions below in ascending order. Explain how you decided. (The point of this problem is to think more and compute less!): \[\frac{2}{5}, \qquad \frac{1}{3}, \qquad \frac{5}{8}, \qquad \frac{1}{4}, \qquad \frac{2}{3}, \qquad \frac{3}{4}, \qquad \frac{4}{7} \ldotp \nonumber \]
Which of these fractions has the larger value? Justify your choice. \[\frac{10001}{10002} \qquad or \qquad \frac{10000001}{10000002} \ldotp \nonumber \]
Solve each division problem. Look for a shortcut, and explain your work.
\[\frac{251+251+251+251}{4} \nonumber \]
\[\frac{377+377+377+377+377}{5} \nonumber \]
\[\frac{123123+123123+123123+123123+123123+123123}{3} \nonumber \]
Yoko says
\[\frac{16}{64} = \frac{1}{4} \nonumber \]
because she cancels the sixes:
\[\frac{16}{64} = \frac{1}{4} \ldotp \nonumber \]
But note:
\[\frac{16}{64} = \frac{1 \cdot 16}{4 \cdot 16} = \frac{1}{4} \nonumber \]
So is Yoko right? Does her cancelation rule always work? If it does not always work, can you find any other example where it works? Can you find every example where it works?
Jimmy says that a fraction does not change in value if you add the same amount to the numerator and the denominator. Is he right? If you were Jimmy’s teacher, how would you respond?
- Shelly says that if \(ab < cd\) then \(\frac{a}{b} < \frac{c}{d}\). Is Shelly’s claim always true, sometimes true, or never true? If you were Shelly’s teacher, what would you say to her?
- Rob says that if \(ad < bc\) then \(\frac{a}{b} < \frac{c}{d}\). Is Rob’s claim always true, sometimes true, or never true? If you were Rob’s teacher, what would you say to him?
Jill, her brother, and another partner own a pizza restaurant. If Jill owns \(\frac{1}{3}\) of the restaurant and her brother owns \(\frac{1}{4}\) of the restaurant, what fraction does the third partner own?
John spent a quarter of his life as a boy growing up, one-sixth of his life in college, and one-half of his life as a teacher. He spent his last six years in retirement. How old was he when he died?
Nana was planning to make a red, white, and blue quilt. One-third was to be red and two-fifths was to be white. If the area of the quilt was to be 30 square feet, how many square feet would be blue?[1]

Ku’u Hae Aloha (My Beloved Flag), Hawaiian cotton quilt from Waimea, before 1918, Honolulu Academy of Arts.
Rafael ate one-fourth of a pizza and Rocco ate one-third of it. What fraction of the pizza did they eat?
Tangrams[2] are a seven-piece puzzle, and the seven pieces can be assembled into a big square.

- If the large square shown above is one whole, assign a fraction value to each of the seven tangram pieces. Justify your answers.
- The tangram puzzle contains a small square. If the small square (the single tangram piece) is one whole, assign a fraction value to each of the seven tangram pieces. Justify your answers.
- The tangram set contains two large triangles. If a large triangle (the single tangram piece) is one whole, assign a fraction value to each of the seven tangram pieces. Justify your answers.
- The tangram set contains one medium triangle. If the medium triangle (the single tangram piece) is one whole, assign a fraction value to each of the seven tangram pieces. Justify your answers.
- The tangram set contains two small triangles. If a small triangle (the single tangram piece) is one whole, assign a fraction value to each of the seven tangram pieces. Justify your answers
Mikiko said her family made two square pizzas at home. One of the pizzas was 8 inches on each side, and the other was 12 inches on each side. Mikiko ate \(\frac{1}{4}\) of the small pizza and \(\frac{1}{12}\) of the large pizza. So she said that she ate
\[\frac{1}{4} + \frac{1}{12} = \frac{3}{12} + \frac{1}{12} = \frac{4}{12} = \frac{1}{3} \nonumber \]
of a pizza. Do you agree with Mikiko’s calculation? Did she eat \(\frac{1}{3}\) of a whole pizza? Carefully justify your answer. (This question is tricky. It’s probably a good idea to draw a picture!)
Look at the triangle of numbers. There are lots of patterns here! Find as many as you can. In particular, try to answer these questions:
- What pattern describes the first number in each row?
- How is each fraction related to the two fractions below it?
- Can you write down the next two rows of the triangle?

Marie made a sheet cake at home, but she saved some to bring to work and share with her co-workers the next day. Answer these questions about Marie’s cake. (Draw a picture!)
- Suppose Marie saved \(\frac{1}{2}\) of the cake for her co-workers and the co-workers ate \(\frac{3}{4}\) of this. What fraction of the entire cake did they eat?
- What if Marie saved \(\frac{1}{6}\) instead, and they ate \(\frac{2}{3}\) of this?
- What if she saved \(\frac{5}{7}\) of the cake and they ate \(\frac{1}{2}\) of this?
An elementary school held a “Family Math Night” event, and 405 students showed up. Two-thirds of the students who showed up won a door prize. How many students won prizes?
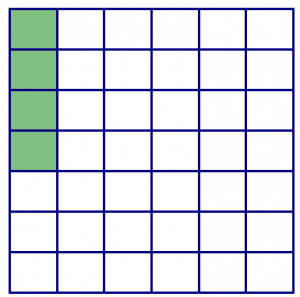
For each picture shown:
- What multiplication problem is represented?
- What is the product?

For each problem, use only the digits 0, 1, 2,. . . , 9 at most once each in place of the variables. Find the value closest to 1. Note that can be a different value in each of the three problems. Justify your answer: How do you know it is the closest to 1?
- $$\frac{a}{b} \ldotp$$
- $$\frac{a}{b} \cdot \frac{c}{d} \ldotp$$
- $$\frac{a}{b} \cdot \frac{c}{d} \cdot \frac{e}{f} \ldotp$$
A town plans to build a community garden that will cover \(\frac{2}{3}\) of a square mile on an old farm. One side of the garden area will be along an existing fence that is \(\frac{3}{4}\) of a mile long. If the garden is a rectangle, how long is the other side?
Nate used \(90 \frac{1}{2}\) pounds of seed to plant \(\frac{1}{4}\) acres of wheat. How many pounds of seed did he use per acre?
The family-sized box of laundry detergent contains 35 cups of detergent. Your family’s machine requires \(1 \frac{1}{4}\) cup per load. How many loads of laundry can your family do with one box of detergent?
Jessica bikes to campus every day. When she is one-third of the way between her home and campus, she passes a grocery store. When she is halfway to school, she passes a Subway sandwich shop. This morning, Jessica passed the grocery store at 8:30am, and she passed Subway at 8:35am. What time did she get to campus?
If you place a full container of flour on a balance scale and place on the other side a \(\frac{1}{3}\) pound weight plus a container of flour (the same size) that is \(\frac{3}{4}\) full, then the scale balances. How much does the full container of flour weigh?

Geoff spent \(\frac{3}{4}\) of his allowance on a movie. He spent \(\frac{11}{18}\) of what was left on snacks at school. He also spent $3 on a magazine, and that left him with \(\frac{1}{24}\) of his total allowance, which he put into his savings account. How much money did Geoff save that week?
Lily was flying to San Francisco from Honolulu. Halfway there, she fell asleep. When she woke up, the distance remaining was half the distance traveled while she slept. For what fraction of the trip was Lily asleep?
- Image used under Creative Commons CC0 1.0 Universal Public Domain Dedication. ↵
- Tangram image from Wikimedia Commons, public domain. ↵


