2.6: The Vector Projection of One Vector onto Another

Last updated
Save as PDF

Page ID: 125033

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Projection

Let’s project vector $\overrightarrow{u}\boldsymbol{=}\left\langle u_x,\left.u_y\right\rangle \right.$ onto the vector $\overrightarrow{v}\boldsymbol{=}\left\langle v_x,\left.v_y\right\rangle \right.$.

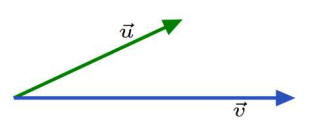
$Image of two vectors, one projecting onto the other. Vectors u and v are connected together by their starting points.$

To do so, imagine a light bulb above $\overrightarrow{u}$ shining perpendicular onto $\overrightarrow{v}$.

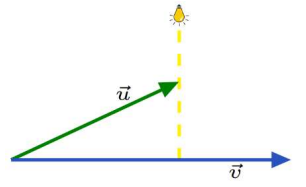
$Image of two vectors, u and v, one projecting onto the other, and a light bulb shining perpendicular above vector u onto v with a dotted yellow vertical line that touches the terminal point of u.$

The light from the bulb will cast a shadow of $\overrightarrow{u}$ onto $\overrightarrow{v}$, and it is this shadow that we are looking for. The shadow is the projection of $\overrightarrow{u}$ onto $\overrightarrow{v}$.

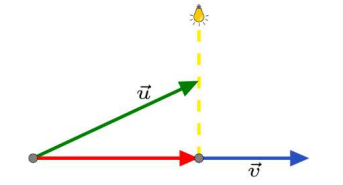
$Image of two vectors, one projecting onto the other, and a light bulb casting a shadow onto the vector creating the projection of one vector onto another. A dotted yellow vertical line touches the terminal point of u. The starting point of u touches the starting point of the red vector. The terminal point of the red vector touches the starting point of the yellow vertical dotted vector. The starting point of the yellow vertical dotted vector touches the starting point of vector v. It is important to note that vector v is parallel to the red horizontal vector.$

The red vector is the projection of $\overrightarrow{u}$ onto $\overrightarrow{v}$. The notation commonly used to represent the projection of $\overrightarrow{u}$ onto $\overrightarrow{v}$ is ${\mathrm{proj}}_{\overrightarrow{\mathrm{v}}}\overrightarrow{u}$.

Vector parallel to $\overrightarrow{v}$ with magnitude $\frac{\overrightarrow{u}\bullet \overrightarrow{v}}{\left\|\overrightarrow{v}\right\|}$ in the direction of $\overrightarrow{v}$ is called projection of $\overrightarrow{u}$ onto $\overrightarrow{v}$.

The formula for ${\mathrm{proj}}_{\overrightarrow{\mathrm{v}}}\overrightarrow{u}$ is

\[\operatorname{proj}_{\overrightarrow{\mathrm{v}}} \vec{u}=\frac{\vec{u} \cdot \vec{v}}{\|\vec{v}\|^2} \vec{v} \nonumber \]

Example $\PageIndex{1}$

To find the projection of $\vec{u}=\langle 4,3\rangle$ onto $\vec{v}=\langle 2,8\rangle$, we need to compute both the dot product of $\overrightarrow{u}$ and $\overrightarrow{v}$, and the magnitude of $\overrightarrow{v}$, then apply the formula.

Solution

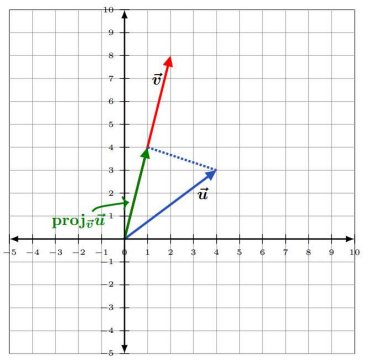
$An image showing an example of two vectors projecting onto another. Both the starting point of projection of (vector u onto vector v) and the starting point of vector v are connected together at (0,0). A dotted line connects the terminal points of the projection of (vector u onto vector v) and vector v. The starting point of vector v is connected to the terminal point of the projection of (vector u onto vector v). Vector v is also parallel to the projection of (vector u onto vector v).$

$\begin{gathered}
\operatorname{proj}_{\overrightarrow{\mathrm{v}}} \vec{u}=\frac{\vec{u} \cdot \vec{v}}{\|\vec{v}\|^2} \vec{v} \\
\operatorname{proj}_{\vec{v}} \vec{u}=\frac{\langle 4,3\rangle \cdot\langle 2,8\rangle}{\|\langle 2,8\rangle\|^2}\langle 2,8\rangle \\
\operatorname{proj}_{\overrightarrow{\mathrm{v}}} \vec{u}=\frac{4 \cdot 2+3 \cdot 8}{\left(\sqrt{2^2+8^2}\right)^2}\langle 2,8\rangle \\
\operatorname{proj}_{\vec{v}} \vec{u}=\frac{32}{(\sqrt{4+64})^2}\langle 2,8\rangle \\
\operatorname{proj}_{\vec{v}} \vec{u}=\frac{32}{68}\langle 2,8\rangle \\
\operatorname{proj}_{\vec{v}} \vec{u}=\frac{8}{17}\langle 2,8\rangle \\
\operatorname{proj}_{\vec{v}} \vec{u}=\left\langle\frac{16}{17}, \frac{64}{17}\right\rangle
\end{gathered}$

Using Technology

We can use technology to determine the projection of one vector onto another.

Go to www.wolframalpha.com.

To find the projection of $\overrightarrow{u}=\left\langle 4,\left.3\right\rangle \right.$ onto $\vec{v}=\langle 2,8\rangle$, use the “projection” command. In the entry field enter projection of $\mathrm{<}$4, 3$\mathrm{>}$ onto $\mathrm{<}$2, 8$\mathrm{>}$.

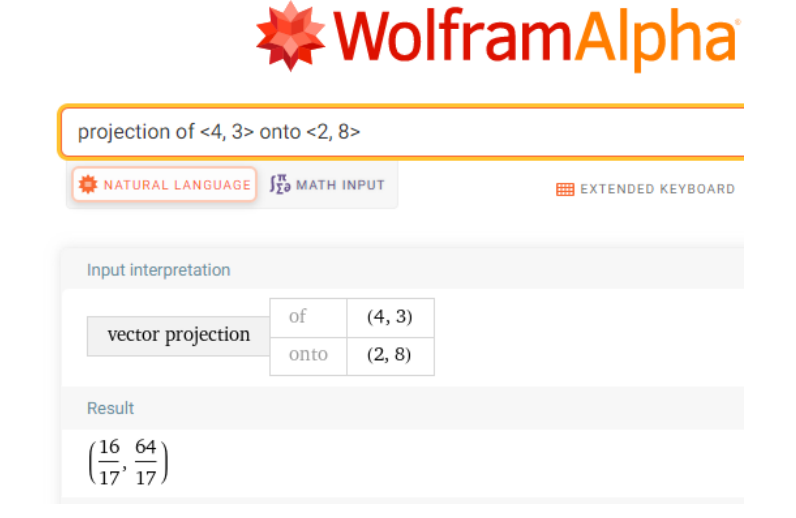$This image from Wolfgang Alpha shows the projection of <4.3> onto <2,8>$ \\

Wolfram alpha tells you what it thinks you entered, then tells you its answer. In this case, $\left\langle \frac{16}{17},\left.\frac{64}{17}\right\rangle \right.$.

Example $\PageIndex{2}$

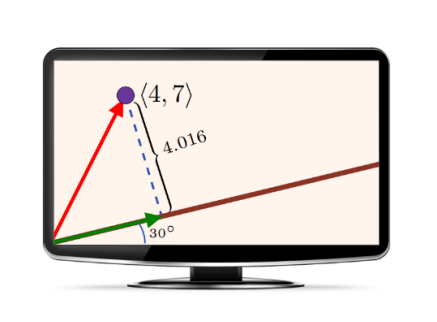
As an applied example, suppose a video game has a ball moving near a wall.

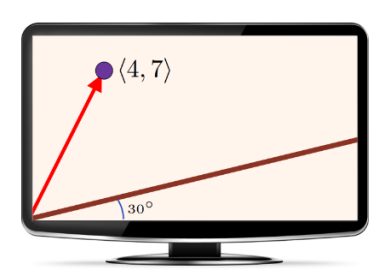
$clipboard_ef900de4e74c5d904f2a7a37e771af9cd.png$

Solution

We take the origin at the bottom-left-most corner of the screen. The wall is at a 30$\mathrm{{}^\circ}$ angle to the horizontal, and at a point in time, the ball is at position $\overrightarrow{v}\boldsymbol{=\ }$$\mathrm{\langle }$4,$\ \left.7\right\rangle$. To find the perpendicular distance from the ball to the wall, we use the projection formula to project the vector $\overrightarrow{v}\boldsymbol{=\ }$$\mathrm{\langle }$4,$\ \left.7\right\rangle$ onto the wall.

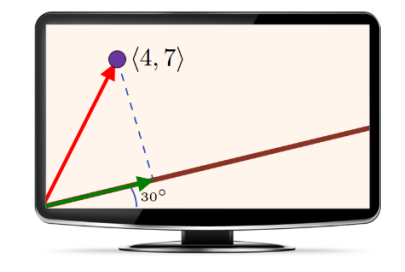
$is connected to the bottom left of the screen as well, with the ball connected to the terminal point of <4,7>. There is a green vector that is 30 degrees away from the bottom of the screen. There is also a dotted line that connects both the terminal points of <4,7> and the green vector together. Finally, there is a brown line that connects the terminal point of the green vector and the right side of the screen. This brown line is parallel to the green vector."$

We begin by decomposing $\overrightarrow{v}$ into two vectors ${\overrightarrow{v}}_1$ and ${\overrightarrow{v}}_2$ so that $\overrightarrow{v}=\ {\overrightarrow{v}}_1+{\overrightarrow{v}}_2$ and ${\overrightarrow{v}}_1$ lies along the wall.

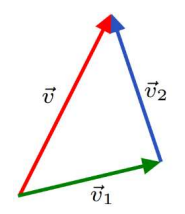
$An illustration showing vector decompose into two vectors creating a triangle. The starting points of vector v and vector v_1 are connected together. The terminal points of vector v and vector v_2 are connected together. The terminal point of v_1 is connected to the starting point of v_2.$

The length (magnitude) of the vector $\overrightarrow{v}$ is then the distance from the ball to the wall.

The vector ${\overrightarrow{v}}_1$ is the projection of $\overrightarrow{v}$ onto the wall. We can get ${\overrightarrow{v}}_1$ by scaling (multiplying) a unit vector $\overrightarrow{w}$ that lies along the wall and, thus, along with ${\overrightarrow{v}}_1$.

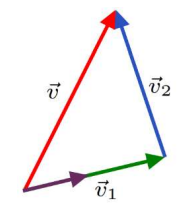
$An illustration showing vector decompose into two vectors creating a triangle with addition of a projection. The starting points of vector v and the purple vector are connected together. The terminal points of vector v and vector v_2 are connected together. The terminal point of the purple vector is connected to the starting point of v_1 and they are both parallel to each other. The terminal point of v_1 is connected to the starting point of v_2.$

Since $\overrightarrow{w}$ lies at a 30$\mathrm{{}^\circ}$ angle to the horizontal, $\overrightarrow{w}\boldsymbol{=}\left.\boldsymbol{\langle }\mathrm{cos}30{}^\circ ,\ \ \mathrm{sin}30{}^\circ \right\rangle \boldsymbol{=}\left.\boldsymbol{\langle }\mathrm{0.866},\ \mathrm{0.5}\right\rangle$, using the projection formula, we get the projection of $\overrightarrow{v}$ that lies along the wall.

$\begin{gathered}
\vec{v}_1=\operatorname{proj}_{\vec{w}} \vec{v}=\frac{\vec{v} \cdot \vec{w}}{\|\vec{w}\|^2} \vec{w} \\
\vec{v}_1 \frac{\langle 4,7\rangle \cdot\langle 0.866,0.5\rangle}{\left\|\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\right\|^2}\langle 0.866,0.5\rangle =\frac{4 \cdot(0.866)+7 \cdot(0.5)}{\left(\sqrt{(0.866)^2+(.5)^2}\right)^2}\langle 0.866,0.5\rangle \\
\vec{v}_1=\frac{6.964}{(\sqrt{1})^2}\langle 0.866,0.5\rangle\\
\vec{v}_1=(6.964)\langle 0.866,0.5\rangle \\
\vec{v}_1=\langle 6.031,3.482\rangle
\end{gathered}$

Since that $\vec{v}=\vec{v}_{\mathbf{1}}+\vec{v}_{\mathbf{2}}$, subtraction get us

$\begin{gathered}
\vec{v}_2=\vec{v}-\vec{v}_1 \\
\vec{v}_2=\langle 4,7\rangle-\langle 6.031,3.482\rangle \\
\vec{v}_2=\langle 4-6.031,7-3.482\rangle \\
\vec{v}_2=\langle-2.031,3.518\rangle
\end{gathered}$

To get the magnitude of $\vec{v}_2$, we use

$\begin{gathered}
\left\|\vec{v}_2\right\|=\sqrt{v_x^2+v_y^2} \\
\left\|\overrightarrow{\boldsymbol{v}}_2\right\|=\sqrt{(-2.031)^2+3.518^2} \\
\left\|\vec{v}_2\right\|=\sqrt{4.125+12.376} \\
\left\|\overrightarrow{\vec{v}_2}\right\|=4.062
\end{gathered}$

$clipboard_ebdf2d24c9adc8ff92aba49b95d3b1f12.png$

Try These

Exercise $\PageIndex{1}$

Find the projection of the vector $\vec{v}=\langle 3,5\rangle$ onto the vector $\vec{u}=\langle 6,2\rangle$.

Answer: $\left\langle \frac{21}{5}\right.,\ \left.\frac{7}{5}\right\rangle$

Exercise $\PageIndex{2}$

Find $\operatorname{proj}_{\vec{v}} \vec{u}$, with $\vec{u}=\langle-2,5\rangle$ and $\vec{v}=\langle 6,-5\rangle$.

Answer: $\left\langle \frac{-222}{61}\right.,\ \left.\frac{185}{61}\right\rangle$

Search

Example \(\PageIndex{1}\)

Solution

Example \(\PageIndex{2}\)

Solution

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)