3.1: Three Dimensional Vectors
- Page ID
- 125035
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
3-Dimensional Space
To this point, we have been working with vectors in 2-dimenisional space. Now, we will expand our discussion to 3-dimensional space.
The 2-dimensional coordinate system is built around a set of two axes that intersect at right angles and one particular point called the origin. Points in the plane are described by ordered pairs \((x, y)\) and vectors in standard position by \(\langle x, y\rangle\).
The 3-dimensional coordinate system is built around a set of three axes that intersect at right angles and one particular point again called the origin. Points in the plane are described by ordered triples \((x, y, z)\) and vectors in standard position by \(\langle x, y, z\rangle\).

The Distance between two Points in 2 & 3-Dimensional Space
In two-dimensional space, the distance \(d\) between two points say \(P(x_1,y_1)\) and \(Q(x_2,y_2)\) is given by the distance formula

\[d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \nonumber \]
In three-dimensional space, the distance \(d\) between two points say \(P(x_1,y_1,z_1)\) and \(Q(x_2,y_2,z_2)\) is given by the distance formula
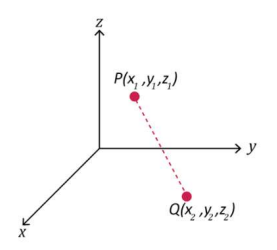
\[d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2} \nonumber \]
The distance between the two points \(P(2,\ 2,\ 5)\) and \(Q(5,\ 6,\ 2)\) is
Solution

\(\begin{gathered}
d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2} \\
d=\sqrt{(5-2)^2+(6-2)^2+(2-5)^2} \\
d=\sqrt{(3)^2+(4)^2+(-3)^2} \\
d=\sqrt{9+16+9} \\
d=\sqrt{34} \approx 5.8 \text { units }
\end{gathered}\)
The distance between the two points \(P(2,\ 2,\ 5)\) and \(Q(5,\ 6,\ 2)\) is \(\sqrt{34}\) \(\approx 5.8\\)units.
Using Technology
We can use technology to find the distance between points.
Go to www.wolframalpha.com.
To find the distance between the two points \((-3,\ 5)\) and \((-7,\ 4)\) enter distance \((-3,\ 5)\) and \((-7,\ 4)\) in the entry field. Wolframalpha tells you what it thinks you entered, then tells you its answer. In this case, \(\sqrt{17}\ \approx 4.1\)2311.

The Equation of a Circle and a Sphere
We can use the distance formulas to get equations of circles and spheres.
The center-radius form of a circle with center at the point \(C(h,k)\) and radius \(r\) is

\[(x-h)^2+(y-k)^2=r^2 \nonumber \]
The center-radius form of a sphere with center at the point \(C(h,k,j)\) and radius \(r\) is

\[(x-h)^2+(y-k)^2+(z-j)^2=r^2 \nonumber \]
To write the equation of a circle that has the point \(C\left(4,\ 7\right)\) as its center and radius 8, we use the center-radius form \({\left(x-h\right)}^2+{\left(y-k\right)}^2=r^2\) with \(h=4\), \(k=7\), and \(r=8\).
Solution
\(\begin{aligned}
& (x-h)^2+(y-k)^2=r^2 \\
& (x-4)^2+(y-7)^2=8^2 \\
& (x-4)^2+(y-7)^2=64
\end{aligned}\)
To write the equation of a sphere that has the point \(C\left(4,\ 7,\ 1\right)\) as its center and radius 8, we use the center-radius form \({\left(x-h\right)}^2+{\left(y-k\right)}^2+\ {\left(z-j\right)}^2=r^2\) with \(h=4\), \(k=7\), \(j=1\), and \(r=8\).
Solution
\(\begin{aligned}
& (x-h)^2+(y-k)^2+(z-j)^2=r^2 \\
& (x-4)^2+(y-7)^2+(z-1)^2=8^2 \\
& (x-4)^2+(y-7)^2+(z-1)^2=64
\end{aligned}\)
Try These
Find the distance between the two points (2,4) and (-3,6). Round to one decimal place.
- Answer
-
\(\sqrt{29}\ \approx 5.4\) units
Find the distance between the two points (-3,5,-6) and (7,-4,2). Round to one decimal place.
- Answer
-
\(7\sqrt{5}\ \approx 15.6\) units
Write the equation of a circle that has the point C(2,9) as its center and radius 1.
- Answer
-
\({\left(x-2\right)}^2+{\left(y-9\right)}^2=1\)
Write the equation of a sphere that has the point C(-2,5,-7) as its center and radius 4.
- Answer
-
\({\left(x+2\right)}^2+{\left(y-5\right)}^2+\ {\left(z+7\right)}^2=16\)

